
今年もバレーボール学会に向けて
今年もそんな季節がやってきたということで、日本バレーボール学会第27大会が来月の3月5日から6に渡ってオンライン形式で開催されます。
今回も一般研究発表にエントリーしますので、その内容のさわりの部分を紹介したいと思います。
サイドアウト率とブレイク率による勝率の予測と実際の勝率との差
一昨年になりますが、同じようにバレーボール学会向けにサイドアウト率とブレイク率による勝率の予測を行いました。
今回の発表では、この予測式を用いて計算された勝率の推定値と実際のチームの勝率との差を求め、この性質を検証したいと思います。
元ネタへと戻る
さて、勝率の推定値と実際の勝率の差という、ずいぶんと細々した値をテーマと選んだわけですが、当然理由があります。
これを説明するには、サイドアウト率とブレイク率による勝率の予測の元ネタである、野球での勝率の予測の話をする必要があります。
野球では、ピタゴラス勝率(得点2/(得点2 + 失点2))という勝率を予測する方法があります。
このピタゴラス勝率は、高い精度で勝率を予測できることが知られています。以下の図1に2010年から2019年までのアメリカMLBでのピタゴラス勝率と実際の勝率の関係を示します。

図中の破線はピタゴラス勝率=実際の勝率を表しています。この破線の近くに多くプロットされていることからも、ピタゴラス勝率の精度の高さを見ることができます。
ピタゴラス勝率は単に高精度な予測式であるだけではなく、この制度の高さを利用して、目標となる勝率を定めて、必要な得点増や失点減といったチームの方針を得ることにも利用が可能です。
ピタゴラス勝率と勝率の差とは?
さて、本題です。図1で見たようにピタゴラス勝率の精度は高いですが、100%勝率とは一致するわけではありません。それは当然のことなのですが、このピタゴラス勝率と実際の勝率との間に生じた差について以下のようなことをいう人が出てきました。
「ピタゴラス勝率で予測された勝率以上に勝つということは、采配の効果ではないか?」
確かに、ピタゴラスは得点と失点に相当する勝率といえますから、それ以下、もしくはそれ以上の勝率は、得点と失点以外によってもたらされたと考えることができます。ただ、これを采配の効果と断言できるわけではありません。
ここから、ピタゴラス勝率と実際の勝率の差の性質の分析が始まりました。その結果、いくつかわかったことがあります。以下の図2-1と図2-2に示すように、5点差以上で勝った試合と負けた試合が多いと、ピタゴラス勝率と実際の勝率の差に影響があります。


それほど強い相関ではないのですが、5点差以上で勝った試合が多くなると、勝率の差がマイナス、つまりは実際の勝率がピタゴラス勝率を下回ることが多くなってきます。逆に5点差以上で負けた試合が多くなると、勝率差はプラス、したがって実際の勝率のほうが高くなる傾向があります。
また、以下の図3には、1点差で勝った試合と負けた試合を合計した割合と、この1点差で勝った試合と負けた試合での勝率を示します。
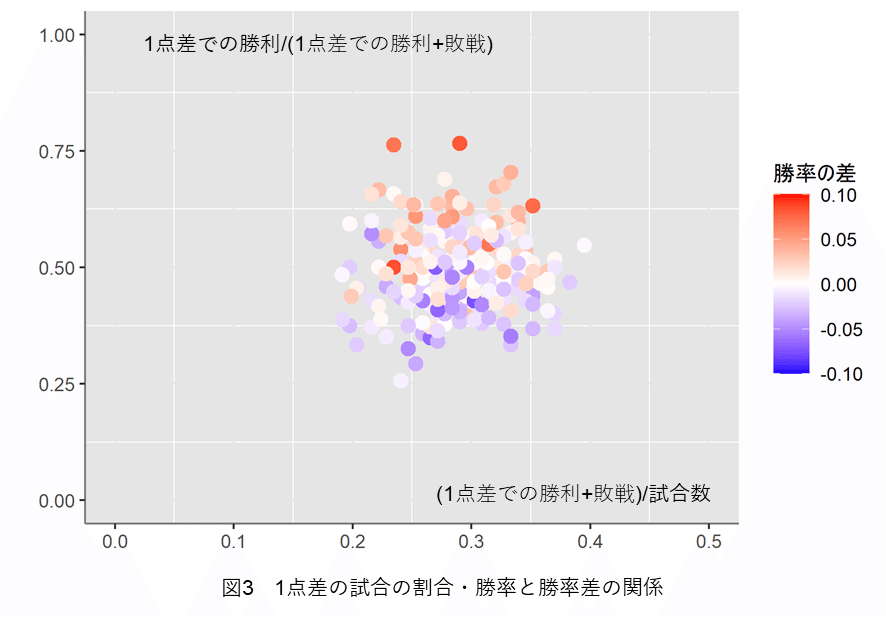
横の軸に1点差の試合の割合を、縦の軸に1点差の試合の勝率を示しています。プロットの色は、実際の勝率からピタゴラス勝率を引いた値に応じて、値がプラスは赤、マイナスは青で、値の絶対値が大きくなるほど色は濃くなります。
図を見ると、上に行くほど濃い赤、下に行くほど濃い青になっており、1点差のゲームで勝敗が、ピタゴラス勝率と実際の勝率の差に影響していることが分かります。
これらの結果は安定するか?
こうした大差、もしくは1点差という接戦での勝敗は采配によるといえるでしょうか?大差での勝敗は采配というよりも、保有戦力の大きさのほうが大きいとは思いますが、接戦を制するのは采配の妙といえる気がします。
そこで、大差と接戦での勝敗のシーズン間の安定性について分析してみたいと思います。シーズン間の安定性を、あるシーズンと次のシーズンの成績の相関から求めます(年度間相関)。
ここで相関が認められれば、シーズン間で安定している、つまりは再現性のある結果ということができます。逆に、相関が認められない場合は、安定した指標とはいえず、運に左右されるコントロールできない結果ということができます。相関が認められないような結果は、采配というよりは運によってもたらされた結果ということができますが、どうなるでしょうか?
まずは、5点差以上の大差で勝敗がついた試合の割合の年度間相関を以下の図4-1-1に示します。

正の相関関係が認められますが、それほど強いものではありません。
次に、1点差の試合の割合と、縦の軸に1点差の試合の勝率の年度間相関を以下の図4-1-2に示します。

こちらでは相関関係は認められません。
次に、前年の成績と、次のシーズンでの成績の変化として、翌年の成績から前年の値を引いたものとの相関を求めました。結果を、以下の図4-2-1と図4-2-2に示します。


ここでは、負の相関関係が認められました。この結果は、あるシーズンの割合が高いと、次のシーズンは低下する。逆に、あるシーズンの割合が低いと次のシーズンは高くなることを表します。
この傾向は、シーズン間で成績が安定していると見られない傾向です。
したがって、大差での勝敗はやや安定しているものの、特に接戦での勝敗は安定した結果とはいえず、運に左右されるコントロールできない結果の特徴をもっているといえます。
データのミスリードは怖い
というわけで、采配の効果のように見えたピタゴラス勝率と実際の勝率の差でしたが、その性質が示すのは、采配によってコントロール可能なものではなく、コントロール不能な運に左右されるものでした。
つまり、ピタゴラス勝率よりも実際の勝率が高いということは、采配が良いわけではなく、単に運が良かったと見る方が妥当であるということです。
このピタゴラス勝率と実際の勝率の差の性質を知らないまま、采配の効果と見てしまうと、幸運なだけの結果を采配の優れた監督と見てしまったり、不運なだけなのに、采配のダメな監督というレッテルを張ってしまうことになります。これは大きな不利益を被ることにつながります。
バレーボールでは?
長々と野球の話になりましたが、バレーボールの勝率の予測式を用いた場合、実際の勝率との差はどのような意味を持っているのだろう?というのが今回の研究テーマとなります。
野球のように、単なる運の良し悪しを采配の効果と間違えてしまうことの無いように、もしかしたら、バレーボールの場合は、本当に采配の効果といる可能性もゼロではありません。さて、データはどのような結果を示すでしょうか?こうご期待。
学会に向けて
こんな感じで発表しようと思います。昨年と一昨年はポスターを預けて終わりだったのですが、今回は2分間のショートプレゼンをすることになりました。ということは、この長々とした前段の話をまとめつつ、データの分析結果を計2分で説明する必要があるということです。割と大変なんじゃないかな。
ショートプレゼン以外にも、やり取りの時間は用意されているようなので、興味のある方はご参加ください。
使用データ
今回の分析で示したデータは以下のリンクより利用が可能です。
図1で示したピタゴラス勝率と実際の勝率の関係は、SeanLahman.comに1871年以降のMLB各チームのシーズンごとの成績が用意されています。
図2以降の、大差や僅差での勝敗のカウントは、RetrosheetのGamelogで試合ごとの結果を1シーズン分に集計しています。
https://www. retrosheet.org/
