(ダイジェスト)10分ちょっとでわかる極配置，拡張誤差適応則，鉄損考慮モデル，MT軸制御，最適励磁制御

以下テンプレ
筆者が開発したVVVFインバータのアルゴリズムについて，その仕組みの一部を少し書きます．筆者はただの素人なので数学的な間違いや物理的意味の誤解などがあるかもしれません．独学なので表現が正しくなかったり一般性を欠いている場合がありますのでご注意ください．ほぼ自分用メモなので変数や記号の定義は割愛させていただきます．

関連項目
(ダイジェスト)10分ちょっとでわかる最大効率追従制御，オブザーバの離散化，スライディングモードのチャタリング排除，完全追従制御，2相変調法

適応2次磁束スライディングモードオブザーバの極配置を工夫することでロバスト化し，ノミナルプラントと実プラントのパラメータミスマッチや運転中のモーターの発熱による1次抵抗と2次抵抗の変動に対しH∞ノルムを抑圧することで低感度化しつつ，また拡張誤差信号を利用して力行回生どちらの領域でも全速度領域で安定して1次抵抗と回転子速度の同時適応をします．

また，鉄損を考慮したモデルを設計し，それに基いた2次磁束の推定と最適励磁制御，鉄損分の電流を考慮し，dq軸座標系から純粋な励磁電流とトルク電流のベクトル分解をしたMT軸座標系による制御をします．

＊極配置＊

先行の複数の研究で，1次抵抗と2次抵抗の変動に対してH∞ノルムを抑圧することで低感度化する極配置の設計法が示されておりますが，それらの方法は適応オブザーバで全速度領域に適用できません．

そこで，適応オブザーバが全速度領域で安定するように，オブザーバの極の設計パラメータαの傾斜を速度が上がるにつれ電気的回転子角速度の絶対値|ω_m|の傾斜に漸近するようにスケジューリングします．

ω_mが極大でαの傾斜が|ω_mΓ|の傾斜と等しくなるようにして導出します．Γはオブザーバゲインの大きさ(傾斜)を決めるパラメータです．以下，ε,c,d,f,A_12,A_22は誘導モーターのモデルのパラメータです．

1次抵抗と2次抵抗の変動に対してロバストな極の設計パラメータαが与えられた時，オブザーバゲインGは

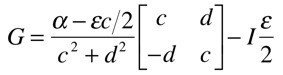
となります．αをオブザーバゲインの大きさ(傾斜)を決めるパラメータΓに基づき

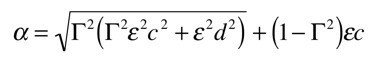
とします．この時，オブザーバの極は

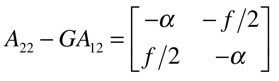
となります．
以上を整理して，オブザーバゲインは

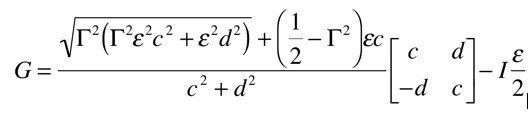
となります．

αの傾斜が|ω_m|の傾斜に漸近する様子(赤:α, 青:|ω_m|, 黒:(α-|ω_m|)×100)

＊拡張誤差適応則＊

誘導モーターの実プラントを

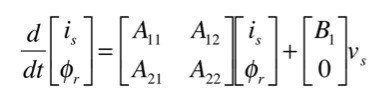
とします．適応2次磁束スライディングモードオブザーバのモデルを

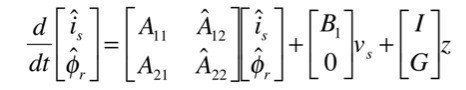
とします．A^_12とA^_22は電気的回転子角速度ω_mを含む適応パラメータです．ここで，zはスライディングモードの特徴であるスイッチング関数を通した電流誤差信号で，スイッチング関数として符号関数を用いて

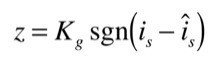
となります．K_gはスイッチングゲインです．

パラメータの誤差から誤差信号zまでの伝達関数は，適応オブザーバから実プラントを引くことで求められます．

スライディングモードが発生し，状態量が切替超平面に拘束されるとi^_s-i_s=0となります．ここから伝達関数を求めます．

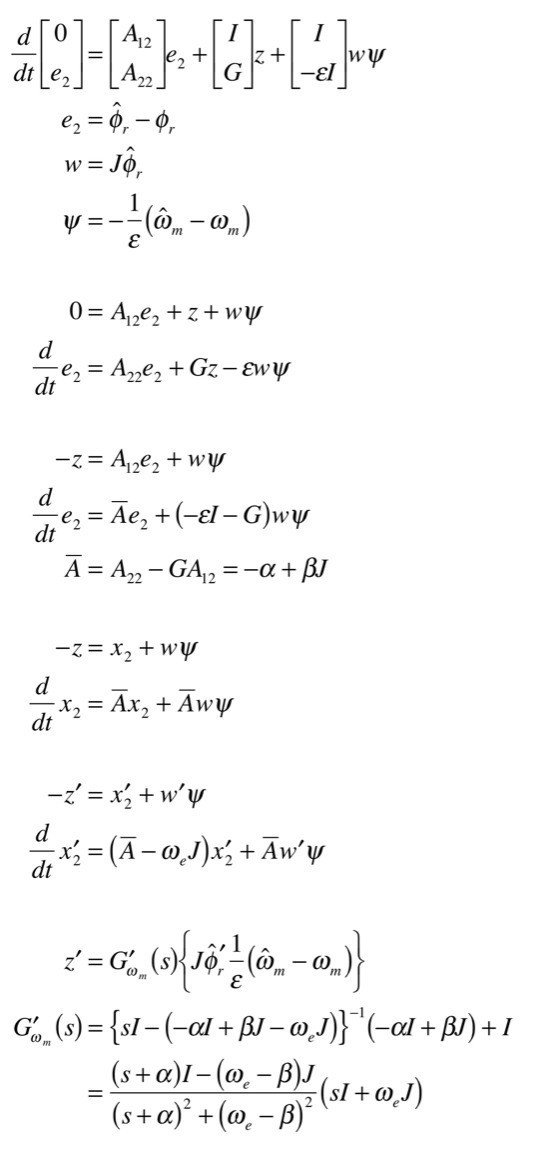
これでω_mの誤差からzまでの伝達関数が求まりました．

続いて，適応2次磁束スライディングモードオブザーバのモデルを

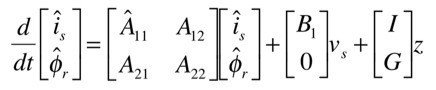
とします．A^_11は1次抵抗R_sを含む適応パラメータです．

引きます．

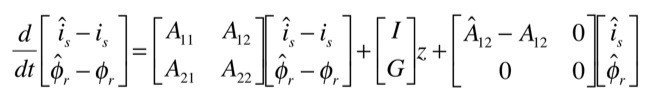
求めます．

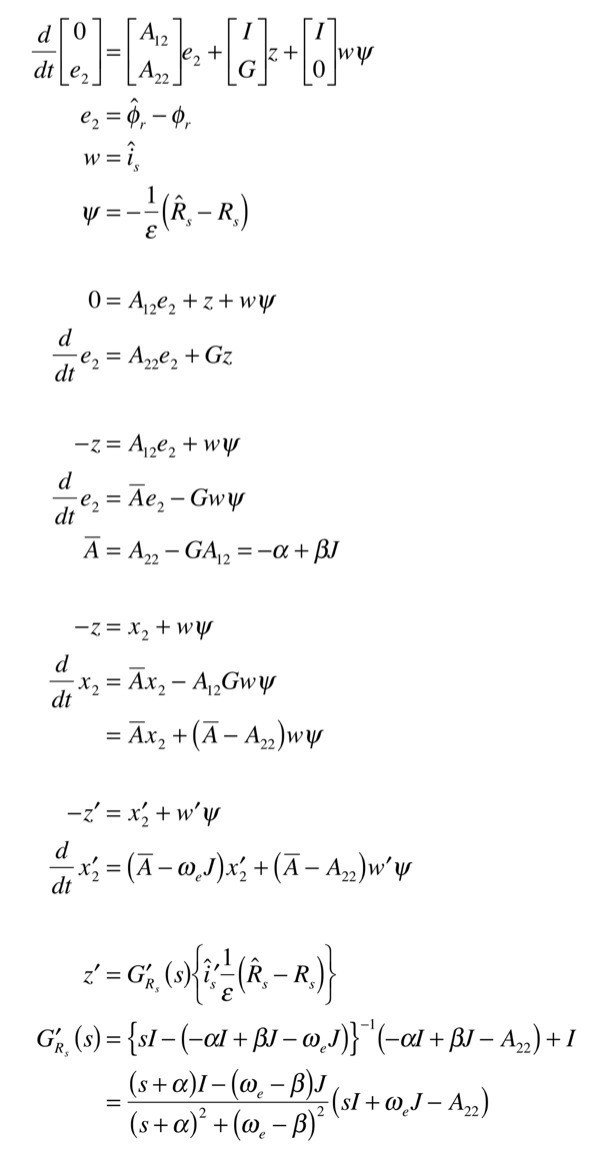
これでR_sの誤差からzまでの伝達関数が求まりました．

ω_mとR_sの誤差は重畳されてzに現れます．

誤差信号zから拡張誤差信号ζを求めます．

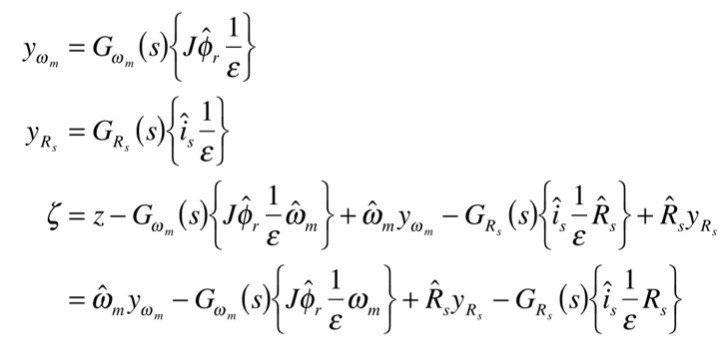
ζから適応パラメータω^_mとR^_sのパラメータ誤差信号Δω^_mとΔR^_sを求めます．

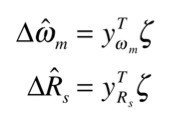
パラメータ誤差信号を用いて適応パラメータを更新(適応)します．K_ω_mとK_R_sは適応ゲインです．

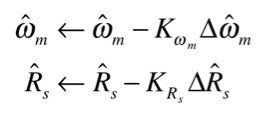
これで力行回生領域どちらでも全速度領域で1次抵抗と回転子速度の同時適応ができます．

尚，単純に適応ゲインを

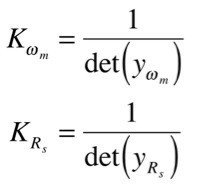
とすると雑音の影響を受けやすくなるので注意が必要です．電源角周波数ω_e=0の時y_ω_m=0となるので除算時に不都合です．

＊鉄損考慮モデル＊

鉄損を考慮した誘導モーターのモデルはT型等価回路ではなく，T-I型等価回路を拡張する形でモデリングしました．T-I型等価回路の相互インダクタンスと並列に抵抗成分として鉄損回路を追加し，モータの定格運転時の定常的な鉄損電力から鉄損抵抗値R_xを計算します．そこから，状態空間表現で式が都合の良い形にするために，相互インダクタンスと直列な抵抗成分R_mとして換算します．

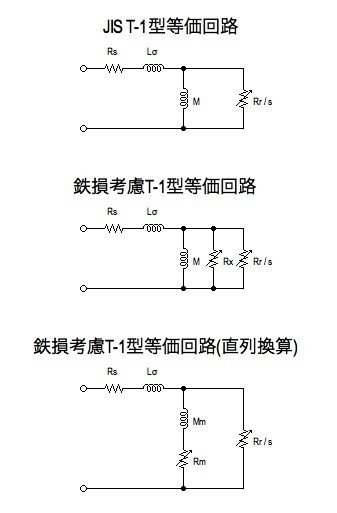
鉄損を考慮した誘導電動機の回転座標上の電圧方程式と状態空間モデルは以下のようになります．a_mは鉄損成分でa_m=R_m/ω_eとなります．鉄損抵抗R_mはリアクタンスのように電源角周波数の関数ですが，ジュール損の成分なのでベクトルは電気抵抗と同じ実軸側になります．鉄損成分a_mは電源角周波数によって変動し，実験的に電源角周波数の約0.6乗に比例します．

2次電流は以下のようになります．

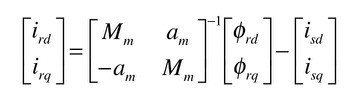
モーターで発生している電気的トルクは以下のようになります．

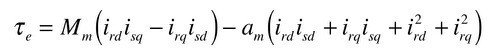
モーターで発生している全ジュール損は以下のようになります．

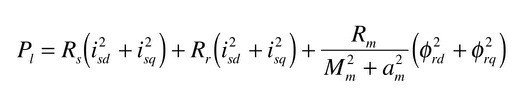
＊MT軸制御＊

ベクトル制御にて

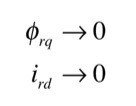
とした時

が成立し，2次磁束指令値φ^*_rdと電気的トルク指令値τ^*_eからMT軸電流指令を

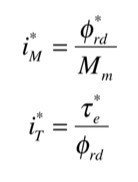
と置き，dq軸電流指令を

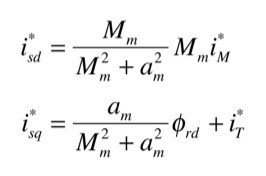
とすると，定常状態に於いて

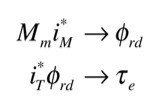
となります．

MT軸による指令は，鉄損を考慮したベクトル制御系に於いて2次磁束とトルクを独立して個別の制御が可能です．

＊最適励磁制御＊

最適励磁制御は、2次磁束の大きさを最適化して誘導モーターを最大効率で運転することです(※水車の最大効率制御ではありません)．モーターで発生する全ジュール損失を最小化するような2次磁束の大きさを指令すればよく，以下のように求まります．

MT軸上に於いて全ジュール損失P_lは

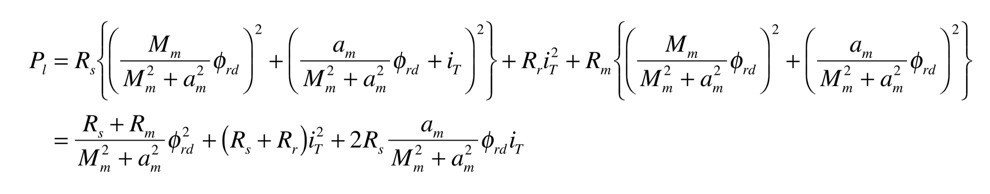
となります．指令トルク電流i^*_Tに基いてP_lが最小となる2次磁束の大きさの解は

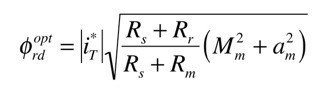
となります．指令磁束を

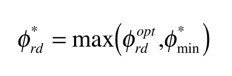
とすれば，鉄損を考慮した誘導モーターの最適励磁制御ができます．φ^*_minは指令磁束の最小値です．誘導モーターは磁束ゼロで運転することは不可能なので，無負荷時にも励磁電流が必要です．実用上，定格の約10%程度の値を設定するのが好ましいと思われます．

#極配置 #適応則 #拡張誤差 #伝達関数 #状態空間 #オブザーバ #スライディングモード #最適励磁制御 #ベクトル制御 #インバータ #誘導モーター