
【素因数分解】覚えておきたい「そろばん式?」素因数分解
私は「Prime Smash !」というゲームを愛しており、時々遊んでいます。
数字を素因数分解するゲームで、大きい数が出てくると難しいですね。
一瞬で素因数分解するのは至難の業ですが、比較的簡単なものもあります。
今回はそろばんの珠の形を使った分解を紹介します。以下で取り上げる数字は、そろばんを習っているからこそ容易に分解できるものではないかと思っています。
尚、そろばんの珠は以下のように表すこととします。長方形の中の横線が梁に対応しており、線の上に色がついていると5玉が使われていることになります。

どんな数が登場するかというと、101や103、107 、109で割り切れる数です。これら4つの数は四つ子素数でしたね。
それでは、私の中の素因数分解のイメージを図で説明していきます。ブロックを分解するような感じですかね…?

2461というそろばんの珠の形を23と161に分けることがポイント。161が23の倍数であることを知っている(23の7倍)ので、
2461=2300+161
=23×100+23×7
=23×(100+7)
=23×107
と分解できるのです。図のようにブロックを分解している感じがして、個人的には素因数分解をしていて気分が良いのです。
(実際はブロックを分解すると下の珠が梁の方へ移動しますが)
他の例も作成しましたので、興味のある方はご覧ください。


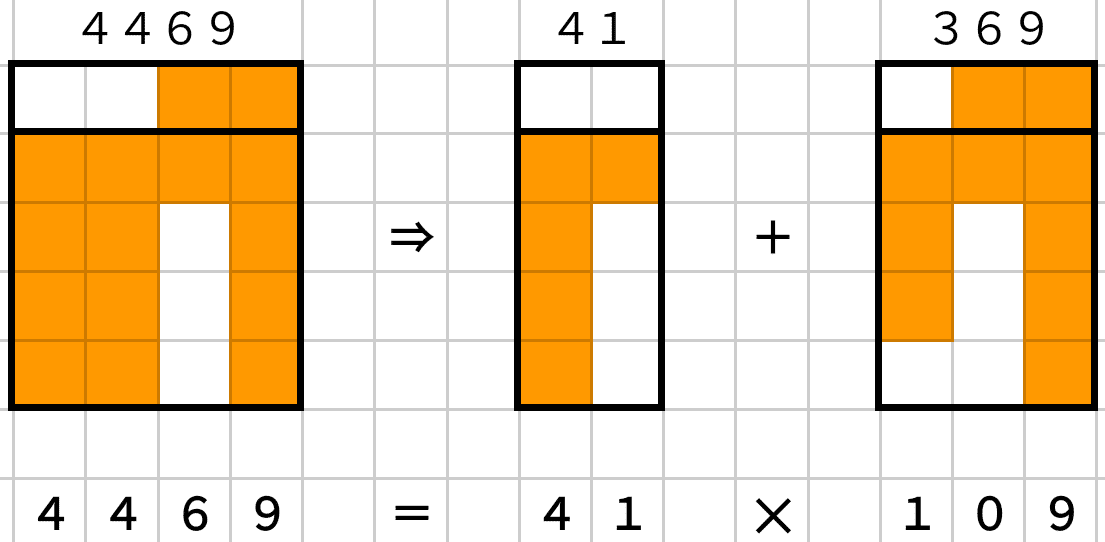


6649を61と549に分けるのは、まさにブロックの分解になっていますね!ぜひとも覚えたい分解です。


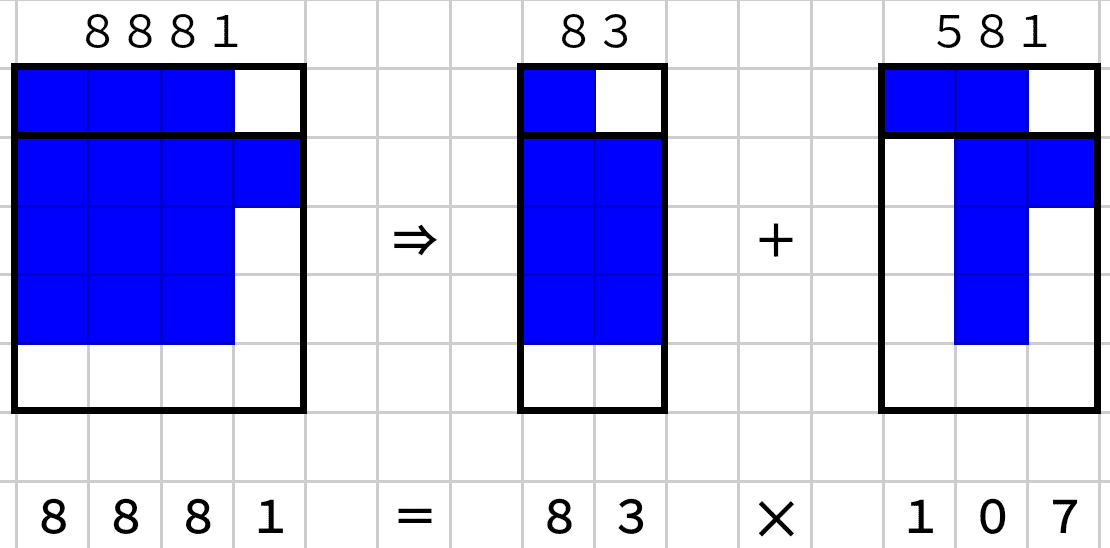

いかがでしたか?
101, 103, 107, 109で割れる数だからこそ、ブロックの分解のイメージで素因数分解ができます。
日常生活で素因数分解をする機会はないかもしれませんが笑、興味のある方は今回の分解方法を覚えていただけたら嬉しいです!
素数はいつも、あなたのそばに。
Let's enjoy SOSU !
最後まで読んでいただき、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
