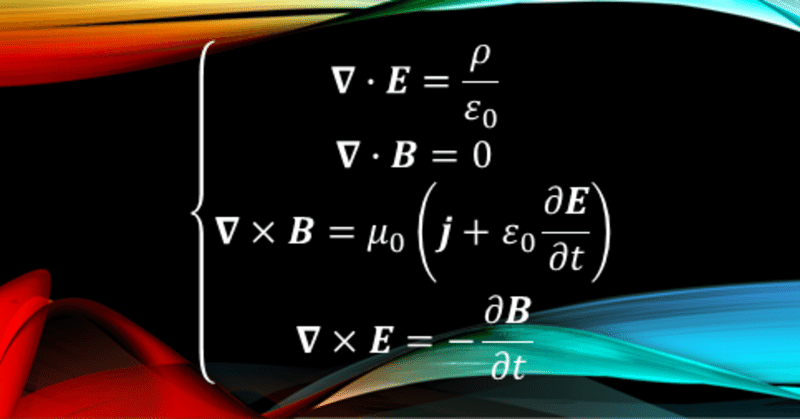
電磁気学② Maxwell方程式の導出

前回の記事はこちら↓

必要な前提知識はこちら↓
・極限と微分，積分(準備中……)
・ベクトル，行列とベクトル解析(準備中……)

電磁気学の第２回です。早くも電磁気学のハイライト，Maxwell(マクスウェル)方程式のお話です。

まずはMaxwell方程式をお見せしましょう

Maxwell方程式は，イギリスのJames Clerk Maxwell(ジェームズ・クラーク・マクスウェル; 1831-1879)が1864年に発表した電磁気学の統一的な方程式です。

後の時代，具体的にはOliver Heaviside (オリヴァー・ヘヴィサイド; 1850-1925)によって，以下のように，ベクトル解析を用いて洗練された形に手直しされました。

$$
\begin{cases}\boldsymbol{\nabla}\cdot\boldsymbol{E}=\dfrac{\rho}{\varepsilon_0}\\\boldsymbol{\nabla}\cdot\boldsymbol{B}=0\\\boldsymbol{\nabla}\times\boldsymbol{B}=\mu_0\left(\boldsymbol{j}+\varepsilon_0\dfrac{\partial\boldsymbol{E}}{\partial t}\right)\\\boldsymbol{\nabla}\times\boldsymbol{E}=-\dfrac{\partial\boldsymbol{B}}{\partial t}\end{cases}
$$

これらの式が何を意味しているのか，また，どのように導かれたのか，以下で見ていきましょう。

Gaussの法則

前回の演習問題で見たように，電場$${\boldsymbol{E}}$$を表す電気力線が領域から出ていく本数と領域に入ってくる本数の差は，領域内にある電荷の量にしたがって変化します。電気量を２倍にすると電気力線の本数も２倍に増えるでしょうから，

「領域から電場が出て行く正味の量は，領域内にある電荷の量$${q_\text{enc}}$$に比例する」

つまり，比例定数を$${\dfrac{1}{\varepsilon_0}}$$($${\varepsilon_0}$$は歴史的経緯から”真空の誘電率”とよばれる)として，

$$
\displaystyle\oiint_{S}\boldsymbol{E}\cdot \boldsymbol{n}\,\mathrm{d}A=\dfrac{q_\text{enc}}{\varepsilon_0}
$$

また，磁場を表す磁束線については，常に領域から出ていく本数と入ってくる本数がつりあっていました。

「磁場は差し引き，外に出ていかない」

つまり，

$$
\displaystyle\oiint_{S}\boldsymbol{B}\cdot \boldsymbol{n}\,\mathrm{d}A=0
$$

これらをGauss(ガウス)の法則といいます。
(注：電場の方の式を“Gaussの法則”，磁場の方の式を“磁場に関するGaussの法則”とよび分ける文献が多いです。)

しかし，この形は不満です。なぜなら，“局所性”という基本原理に反しているからです。具体的には，

①遠くにある電荷の影響を受ける形になっている
②電場や磁場を計算する際，領域の境界面上の1点を除くすべての点での値が与えられたときに限り，1点の電場，磁場が求まる形になっている

の2点が気になります。なんとかして，積分を外したいものです……。

そこで！！

これらを，Gaussの発散定理を用いて変形していきます。
Gaussの発散定理は以下の式で表されます。

$$
\displaystyle\oiint_{\partial V}\boldsymbol{F}\cdot\boldsymbol{n}\,\mathrm{d}A=\iiint_V\boldsymbol{\nabla}\cdot\boldsymbol{F}\,\mathrm{d}\tau
$$

それでは使ってみましょう。

$$
\displaystyle\oiint_{\partial V}\boldsymbol{E}\cdot \boldsymbol{n}\,\mathrm{d}A=\iiint_V\boldsymbol{\nabla}\cdot\boldsymbol{E}\,\mathrm{d}\tau\\\displaystyle\oiint_{\partial V}\boldsymbol{B}\cdot \boldsymbol{n}\,\mathrm{d}A=\iiint_V\boldsymbol{\nabla}\cdot\boldsymbol{B}\,\mathrm{d}\tau
$$

より，Gaussの法則は以下のように書けます。

$$
\displaystyle\iiint_V\boldsymbol{\nabla}\cdot\boldsymbol{E}\,\mathrm{d}\tau=\iiint_V\dfrac{\rho}{\varepsilon_0}\,\mathrm{d}\tau\\\displaystyle\iiint_V\boldsymbol{\nabla}\cdot\boldsymbol{B}\,\mathrm{d}\tau=0
$$

ここで，電荷密度$${\rho}$$というものを導入しました。これは，$${q_\text{enc}=\displaystyle\iiint_V\rho\,\mathrm{d}\tau}$$を満たす物理量です。

局所性の観点から，両辺の積分記号は外すことができます。これで，Maxwell方程式の第１式と第２式を得ることができました。

めでたしめでたし。

Ampèreの法則とFaradayの電磁誘導の法則

話は変わって，電流を考えてみましょう。ある面$${S}$$を貫く電流を$${I_\text{enc}}$$としたとき，電流密度という物理量$${\boldsymbol{j}}$$を，次の式を満たすように定義します。

$$
I_\text{enc}=\displaystyle\iint_S\boldsymbol{j}\cdot\boldsymbol{n}\,\mathrm{d}A
$$

電流の定義式$${\displaystyle I=\dot{(q_0-q)}}$$($${q_0}$$は領域内にもともとあった電気量)を，電荷密度$${\rho}$$と電流密度$${\boldsymbol{j}}$$を用いて表すと，次のようになります($${\dot{q_0}=0}$$を用いています)。

$$
\displaystyle\iint_S\boldsymbol{j}\cdot\boldsymbol{n}\,\mathrm{d}A=-\displaystyle\iiint_V\dot{\rho}\,\mathrm{d}\tau
$$

Gaussの法則から，領域が時間変化しないとき，次の式が成り立ちます。

$$
\boldsymbol{\nabla}\cdot\boldsymbol{j}+\dot{\rho}=0\\
\Leftrightarrow \boldsymbol{\nabla}\cdot\boldsymbol{j}+\dot{\boldsymbol{r}}\cdot\boldsymbol{\nabla}\rho+\dfrac{\partial\rho}{\partial t}=0
$$

いま領域は時間変化しないので，$${\dot{\boldsymbol{r}}=0}$$。したがって，全微分は偏微分に書き換えることができ，一般に，

$$
\boldsymbol{\nabla}\cdot\boldsymbol{j}+\dfrac{\partial\rho}{\partial t}=0
$$

これで，$${\rho}$$と$${\boldsymbol{j}}$$の関係(電荷保存則)が表せました。

ここで，Maxwell方程式の第１式の両辺を時間微分すると，

$$
\boldsymbol{\nabla}\cdot\dfrac{\partial\boldsymbol{E}}{\partial t}=\dfrac{1}{\varepsilon_0}\dfrac{\partial\rho}{\partial t}
$$

電荷保存則の式を使うと，

$$
\boldsymbol{\nabla}\cdot\dfrac{\partial\boldsymbol{E}}{\partial t}=-\dfrac{1}{\varepsilon_0}\boldsymbol{\nabla}\cdot\boldsymbol{j}
$$

したがって，

$$
\boldsymbol{\nabla}\cdot\left(\boldsymbol{j}+\varepsilon_0\dfrac{\partial\boldsymbol{E}}{\partial t}\right)=0
$$

ここで，なめらかな($${\mathrm{C}^1}$$級の)ベクトル関数$${\boldsymbol{F}}$$に関して成り立つ，以下のベクトル解析の公式があります。

$$
\boldsymbol{\nabla}\cdot\boldsymbol{F}=0\Leftrightarrow\exists\,\boldsymbol{G}\ [\boldsymbol{F}=\boldsymbol{\nabla}\times\boldsymbol{G}]
$$

このことから，

$$
\boldsymbol{j}+\varepsilon_0\dfrac{\partial\boldsymbol{E}}{\partial t}=\boldsymbol{\nabla}\times\boldsymbol{G}_1
$$

なんとかして$${\boldsymbol{G}_1}$$を知る手立てはないでしょうか。

……………実験してみればいいですね！

というまでもなく，すでに実験済みでした。
1820年にAndré-Marie Ampère (アンドレ＝マリ・アンペール; 1775-1836)が静磁場(時間変化しない磁場)に関する実験結果をもとに発表した，Ampèreの法則がそれです。

$$
\displaystyle\oint_{C}\boldsymbol{B}\cdot\mathrm{d}\boldsymbol{s}=\mu_0I_\text{enc}
$$

ただし，磁場の向きは電流を右手親指を立てた向きにとったとき，その他の握った指が向く方向(右手の法則)。$${\mu_0}$$は真空の透磁率とよばれる定数です。

Ampèreの法則の式を，次のStokes(ストークス)の定理を使って変形してみます。

$$
\text{Stokesの定理: }\displaystyle\oint_{\partial S}\boldsymbol{F}\cdot \,\mathrm{d}\boldsymbol{s}=\iint_S(\boldsymbol{\nabla}\times\boldsymbol{F})\cdot\boldsymbol{n}\,\mathrm{d}A\\\therefore\displaystyle\iint_S(\boldsymbol{\nabla}\times\boldsymbol{B})\cdot\boldsymbol{n}\,\mathrm{d}A=\mu_0\iint_S\boldsymbol{j}\cdot\boldsymbol{n}\,\mathrm{d}A\\\Leftrightarrow(\boldsymbol{\nabla}\times\boldsymbol{B})\cdot\boldsymbol{n}=\mu_0\boldsymbol{j}\cdot\boldsymbol{n}
$$

ここで$${\boldsymbol{n}=\boldsymbol{e}_x, \boldsymbol{e}_y, \boldsymbol{e}_z}$$を順に代入することで，

$$
\boldsymbol{\nabla}\times\boldsymbol{B}=\mu_0\boldsymbol{j}
$$

あれ？？
さっきの式と比べると，ひとつ項が足りませんね……。

無理矢理取り出せるかな……

えいや！

$$
\boldsymbol{\nabla}\times\boldsymbol{B}+\varepsilon_0\mu_0\dfrac{\partial\boldsymbol{E}}{\partial t}=\mu_0\left(\boldsymbol{j}+\varepsilon_0\dfrac{\partial\boldsymbol{E}}{\partial t}\right)
$$

導出過程から，右辺の発散は0。左辺の発散を計算してみると，

$$
\boldsymbol{\nabla}\cdot\left(\boldsymbol{\nabla}\times\boldsymbol{B}+\varepsilon_0\mu_0\dfrac{\partial\boldsymbol{E}}{\partial t}\right)=\varepsilon_0\mu_0\dfrac{\partial}{\partial t}(\boldsymbol{\nabla}\cdot\boldsymbol{E})=\mu_0\dfrac{\partial\rho}{\partial t}\ne0
$$

したがって，左辺と右辺が等しくないから，時間変化を含んだ形ではAmpèreの法則は成り立ちません。

天下り的ではありますが，$${\boldsymbol{j}\to\boldsymbol{j}+\varepsilon_0\dfrac{\partial\boldsymbol{E}}{\partial t}}$$と考えると，

$$
\boldsymbol{\nabla}\times\boldsymbol{B}=\mu_0\left(\boldsymbol{j}+\varepsilon_0\dfrac{\partial\boldsymbol{E}}{\partial t}\right)
$$

Maxwell方程式の第３式が出てきました。

Maxwell方程式の第２式についても時間微分してベクトル解析の公式を用いると，

$$
\dfrac{\partial\boldsymbol{B}}{\partial t}=\boldsymbol{\nabla}\times\boldsymbol{G}_2
$$

ここで，$${\boldsymbol{G}_2}$$を知るのにFaraday(ファラデー)の電磁誘導の法則を用います。

$$
\displaystyle\oint_{C}\boldsymbol{E}\cdot\mathrm{d}\boldsymbol{s}=-\dfrac{\partial}{\partial t}\iint_S\boldsymbol{B}\cdot\boldsymbol{n}\,\mathrm{d}A
$$

ただし，電場の向きは磁場が変化する向きに対して右手の法則に従います。領域が時間変化しないと仮定して，この式をStokesの定理を使って変形すると，

$$
\boldsymbol{\nabla}\times\boldsymbol{E}=-\dfrac{\partial\boldsymbol{B}}{\partial t}
$$

が得られます。
$${\boldsymbol{G}_2=-\boldsymbol{E}}$$は問題なさそうです。

長い道のりでしたが，ここまでで，Maxwell方程式を導くことができました。

今回はここまでです！
ありがとうございました。

電磁気学編　目次
① 電磁気学とは何か
② Maxwell方程式の導出　←今ココ！
③ 真空中の静電場・静磁場
④ 静電場・静磁場とエネルギー
⑤ 物質中の電場
⑥ 物質中の磁場
⑦ 電磁場のエネルギー
⑧ 電磁波
⑨ 電気回路
⑩ 相対論と電磁気学
◼︎ 章末問題