小学生への算数教育について思うこと
全般的に思うこと
教育している内容全般については大きな問題はないように思っています。
これは中学受験がそこまで一般的ではないことに起因していると考えています。
受験を意識すると、皆があまり点数を取れない分野を考える必要性が発生し、受験算数というものが発生するものと考えています。
ただ計算ドリルを多く解かせる必要性はより減少していくものと思います。道具の進歩により、ますます単純な計算を手で行うことはすくなくなるためです。
またプログラミング教育も急がなくてよいと私は考えています。中学生で変数に慣れてからでも、プログラムの変数とは異なる面があることを意識しつつ学べばいいと思います。
本当に興味がある子は、パソコンを与える等環境の準備だけしておけば勝手に学んでいくものです。
ちなみに以下の記事は過去の私の意見を記載した記事です。
四則演算について
1.数の認識
算数を始める上で、数について遠山啓 著「数学入門 上」では3つの認識が必要だと記載されています。その3つの認識について、それぞれ例を記載しました
1) 1本の木に縄を付けて縄の数を数えた場合、それは木の数を数えたのと同じであるということ
2) 1箱にクッキー10枚がある場合、その10枚を2箱に分けたとしても全体では10枚であり、数としては変わらないということ
3) 10個のクッキーを1列に並べて数えた時、右から数えても、左から数えても数がかわらないということ
上記の認識は小学校1年生の年齢であれば大体問題なく行えます。
ただ早生まれの子は時間的には不利だと思います。
数学は積み上げの教科のため、無理に次の過程に進むことは、分からないを積み上げていくことになり、「できない」や「嫌い」といった感情を生みやすくなります。
ただ留年させるべきかというと、これも劣等感を生み出しことにつながると思います。
科目を単位制にして、上手くキャッチアップできれば追いつけるようにするといった柔軟性を持たせるのがよいのではないかと考えます。
2.時計と60進法
10進法以外の60進法の世界を体感でき、かつ実用性もある時計について、現在デジタルが主流です。
現在の子供は針の軌跡が円を描く時計をそもそも見慣れない可能性が高いです。そのため時計を教える際は、当然だと思ってこちらが省きやすい部分(全ての針が常に動いている等)を補足する必要性が出てくると思います。
3.計算順序においてなぜかけ算、割り算が先行するのかという意味
少なくとも私は疑問に思っていてあまり説明を受けなかったように感じる点です。
足し算や引き算は同じ種類のものについて足し引きをします。
例えば (長さ)-(面積) といった計算はほとんど実行されません。
次にかけ算や割り算は計算の結果、新しい種類のものを算出します。
例:(縦の長さ)×(横の長さ)=面積 (距離)÷(速さ)=(時間)
そのためかけ算や割り算を先に行い、種類を揃えた後足し算や引き算が行われることになります。
上記のような点について説明を受けた記憶があまりないので強調してもよい点かと思います。
4.文章題について
文章題は算数と現実の問題をつなぐ大事な分野です。
多くの小学生は以下のように考えていると思います。
問題を読む
足し算、引き算、かけ算、割り算のどれを使うか考える。
引き算の場合、何から何を引くか考える。割り算の場合、何から何を割るか考える。
式を立て、計算し、答えを導き出す。
問題は引き算や割り算は、順序を間違えやすいという点にあります。また自分の個人的な経験から言っても、関係性をとらえる上で足し算やかけ算の方が関係性を間違えにくかったといったことがあります。
方程式を学ぶとより考えやすいのですが、米国の無料で学習できるサイト「カーンアカデミー」を見てみると、問題を図式化するという考え方があったので、取り入れることができればよいなと思いました。

足し算やかけ算で関係性を捉え、分からない数を求めるために引き算や割り算を使用すればよいという点について説明すると以下のようになります。
1)足し算と引き算の関係
(例)Aはリンゴを5個持っている。Bはリンゴを4個持っている。全部で9個のリンゴがある。
足し算としては、以下の関係が成立しています。
(Aのリンゴ:5)+(Bのリンゴ:4)=(全部のリンゴ:9)
引き算としては、以下の2つの関係が成立しています。
(Aのリンゴ:5)=(全部のリンゴ:9)- (Bのリンゴ:4)
(Bのリンゴ:4)=(全部のリンゴ:9)- (Aのリンゴ:5)
引き算とは足し算の相方を求める計算であり、足し算の関係性さえ見えれば何から何を引くべきかといった引き算の式を考えることは容易です。
2)かけ算と割り算の関係
(例)1人にリンゴを5個配ります。4人います。リンゴは全部で20個必要です。
かけ算としては以下の関係が成立しています。
(1人に配る数:5)×(配る人数:4)=(全部で必要な数:20)
割り算としては、以下の2つの関係が成立しています。
(1人に配る数:5)=(全部で必要な数:20)÷(配る人数:4)
(配る人数:4)=(全部で必要な数:20)÷(1人に配る数:5)
割り算とはかけ算の相方を求める計算であり、かけ算の関係性さえ見えれば何から何を割るべきかといった割り算の式を考えることは容易です。
足し算とかけ算の関係性を問題文の中で見つけることができれば、引き算と割り算は自然と立式できることが分かりました。そこで算数の文章題を解くとき以下のように考えることができるというわけです。
問題を読む
足し算、かけ算の関係性を見つける。
求めたいものについての式を立て、計算し、答えを導き出す。
5.割り算の意味について
割り算には等分除と包含除の考え方がある点はもう少し強調して教えておいた方がいいと思います。
割り算としては、以下の2つの関係を紹介しましたが、このように全然違う種類が発生することも割り算に二つの意味があることに起因します。
(1人に配る数:5)=(全部で必要な数:20)÷(配る人数:4)
(配る人数:4)=(全部で必要な数:20)÷(1人に配る数:5)
1)等分除:「1人に配る数」を求める際の考え方です。
全部のリンゴを4人に均等に配るという考え方で、等分しているということになります。
2)包含除:「配る人数」を求める際の考え方です。
全部のリンゴを1人に5個配る場合、5という数のセットが全部のリンゴ 20にどれだけ含まれる(包含される)かという考え方です。
特に包含除の考え方は分数の割り算をなぜひっくり返すかという説明において有効です。
$${3÷\frac{1}{3}=3×3}$$

6.整数の分数を小数にすると、必ず有限小数(割り切れる小数)か無限の循環小数になる説明
例えば 3÷7 を考えます。
余りは0~6の数になります。
0の場合は割り切れることになるので、有限小数になります。
さらに一回でも発生した余りと同じ数が余りになった瞬間、同じ計算が繰り返されることになるので、無限の循環小数になります。
無限の循環小数でない数になるためには毎回異なる余りを出す必要がありますが、7回計算すれば確実に余りのパターンは網羅されることになりますので、回避不可能です。
そのため整数の分数を小数にすると、必ず有限小数か無限の循環小数になるといったことは説明がもう少しあってもよいかなと思う点です。
算数の図形(主に面積)について
大事なことは、1×1の正方形が何個入るかということが面積の根本にあること、そして他の図形から導き出された面積の公式を使っていく感覚だと思います。体積についても同様です。
この点から台形の面積の公式を覚えているかどうかより、どのように算出されているかが分かることの方が大切だと思います。
1.正方形・長方形の面積:(縦の長さ)×(横の長さ)

長方形の中で、4辺の長さが同じ特殊なケースが正方形と考えることができ、長方形の方が広い概念という考え方ができます。
こういった概念の包含関係を教えることができるのは、図形を教えるメリットです
2.平行四辺形の面積:(底辺)×(高さ)

平行四辺形から直角三角形を切り出し、くっつけると長方形になります。そうすると長方形の面積として計算できます。
台形は参考までに記載しましたが、もう一つ用意してひっくり返してくっつけると平行四辺形になります。
このようにすでに求め方を知っている面積を元に考えるということがきちんと伝えることが必要だと思います。
3.三角形の面積:(底辺)×(高さ)÷2

三角形の面積は、2つくっつけるとどのような形でも長方形、正方形、または平行四辺形になります。
そのため同じような公式で表すことができますが、「高さ」は直角に下した線ということが正しく伝えられるかという点が肝になると思います。
4.円の面積:(半径)×(半径)× (円周率)
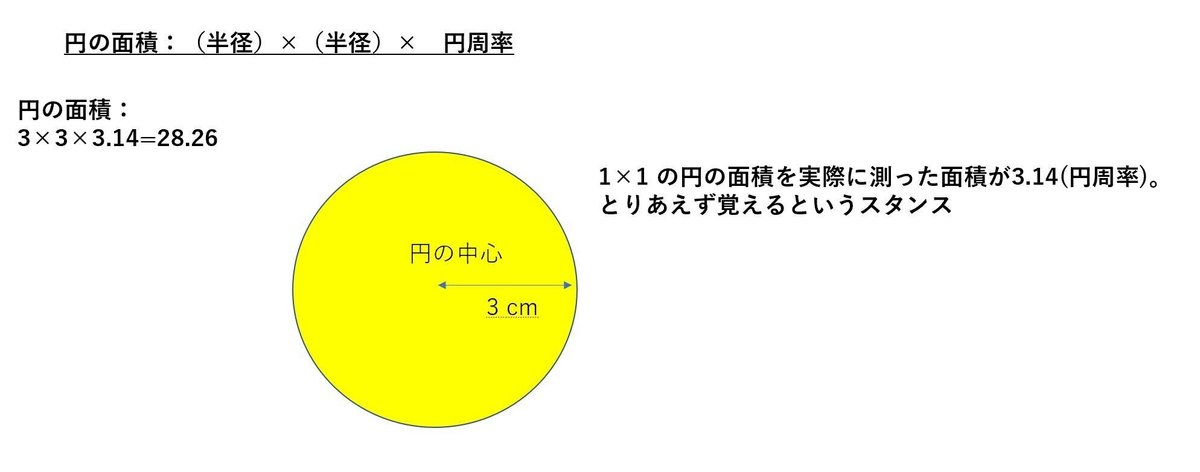
円の面積については、分かりやすく伝えようとするものをいくつか見かけましたが、実際あまり分かりやすいものを見たことはありません。
公式として覚えてもらうというスタンスでいいと思います。
円周率については小学校で実際計算する際には、「3.1」がいいのかなと個人的には考えています。
3のように綺麗な数にはならないというニュアンスと「3.14」まで導入して計算を長くするメリットもそこまでないという点からの意見です。
何か実際に求める必要がある際には、関数電卓かアプリを使用して求めることになるので、そこまで3.14にこだわる必要性はないと考えています。
