世界一わかりにくい算数(小学校3年_数と計算編)
1.日本のカリキュラム
日本のカリキュラムは、整理すると次のようになります。
(以下のサイトを参考にしています。)
内容を私なりにまとめると以下のようになります。
(A.数と計算)
10000までの数を理解し、大小関係や数を固まりで把握する。
加法と減法(4桁や5桁)
乗法(3桁、4桁×1桁、2桁)
除法、小数(1/10)、分数(2/3)
そろばん
そろばんより表計算ソフトや関数電卓に触れたほうがいいとも実務的には思いますが、子供のころは指を使うことで脳への良い刺激を与えられる研究もあるのでこのままでもよいかもしれません。
少し触れてみる程度で、テストまでするかは微妙かなと思います。
2.米国のカリキュラム
世界大学ランキングで上位を占める大学が多い米国を参考にします。
ソースはカーンアカデミーを参考にしています。
3rd gradeと若干 4th grade を参考にしています。
3rd grade
1)わり算入門
2)分数入門
3)かけ算と割り算
4th grade
1)10000 までの位の数
2)かけ算(2ケタ同士等)
3)小数
気づいた点は分数を先に教え、その後小数という形で年次を分けている点です。この2テーマは確かに2学年に分けてじっくりやってもいい点かなと思います。
逆に四捨五入は3年次に導入しています。大体の数を計算することは日常生活でも大事なことなので、早めに概念に触れているのだと思います。
わり算は難しい計算です。式の持つ意味の難しさと答えのむずかしさ、そして数の概念を広げないといけません。
正直大人でもきちんと理解している人が少なく、ここから算数嫌い、数学嫌いになっていきます。
分数の計算でも不思議な計算をするようにもなります。2年かけてじっくり教えるというカリキュラムは合理的判断かもしれません。
3.理解と社会的実践
(1)10000までの数と足し算と引き算になれる
世界一わかりにくい算数(小学校2年_数と計算編)にて「10000(一万)までの数」、「位」、「100~1000までの足し算と引き算」、「かけ算の考え方と九九」について説明しました。
位とケタについて簡単に説明します。
1ケタの数:1から9までの数、2ケタの数:10から99までの数、
3ケタの数:100から999までの数
ここまでの具体例でわかるように、一番大きい位に注目して、それが1の位なら1ケタ、10の位なら2ケタ、100の位なら3ケタとなります。
これはどこまでも続けることができ、4ケタの数:1000から9999、5ケタの数:10000から99999 となります。
足し算や引き算について位が増えてもやることは変わりません。
足し算:「数を分解して同じ位の数を足し算します」
引き算:「数を分解して同じ位の数を引き算します。足りない場合は一つ上の位の数からもらってきます。」
位が増えると、位をミスすることが増え、難しくなったように感じると思います。大事なことはやってることは変わらないと意識することです。
(正直、理系の人や数学者でも計算がそんなに得意でない人が多く存在します。計算能力と算数の思考は別のところにあるのでしょう。)
[算数の問題]
(1)
問題集を3冊買いました。それぞれ1132円、2549円、1800円でした。合計いくら払ったでしょうか。
(2)
問題集を3冊買いに行きます。それぞれ1132円、2549円、1800円でした。
親から5000円もらいました。足りますか。
足りない場合、6000円渡すといわれました。おつりはいくらでしょうか。
(答え)
(1)
(問題集1)+(問題集2)+(問題集3)=(合計金額) となります。
1132+2549+1800
=(1000+100+30+2)+(2000+500+40+9)+(1000+800)
=(1000+2000+1000)+(100+500+800)+(30+40)+(2+9)
=4000+1400+70+11=(4000+1000)+400+(70+10)+1
=5000+400+80+1=5481
5481円となります。
もちろん、1132+2549(=3681) を計算して、その計算結果(3681)に1800を足すという考え方でも計算できます。
(2)
(問題集の合計金額=5481円)>5000円 なので足りません。
そのため6000円もらう必要があります。
(問題集の合計金額)+(おつり)=(親からもらった金額)となりますので、
6000-5481=6000-(5000+400+80+1) <-数の分解
=(6000-5000)-400-80-1 <-同じ位の引き算
=(1000-400)-80-1 =600-80-1
=500+(100-80)-1=520-1 <-100を渡す
=510+(10-1) =519 <-10を渡す
おつりは519円になります。
(2)四捨五入
「問題集を3冊買いに行きます。それぞれ1132円、2549円、1800円でした。親から5000円で足りるか聞かれました。」
これに似たケースは日常生活で起こると思います。この場合、正確な答えがわからなくても大体分かればよいと思うこともあると思います。
例えば、1132円は1100円、2549円は2500円、1800円は1800円として計算すると慣れてくれば暗算で、5400円と計算できると思います。
そうすると5000円では足りなさそうなので、6000円欲しいといえるわけです。
このとき1132円を1000円、2549円を2000円、1800円を1000円として計算すると4000円になるので、5000円で足りるという計算になりますが、実際には足りません。
これは大体の数がわかればよいというケースであっても、ある程度の規則を持って考えなければ「ずれ」が大きくなりすぎてしまうということを意味しています。
そこで出てくる方法が四捨五入と言われるもので、4以下だったら0にして、5以上だったらその位は0にして、その上の位に1を足すという方法です。
また四捨五入をする際には、四捨五入する位以下の数をすべて 0にします。
例えば、2549の百の位を四捨五入してくださいと言われた場合、百の位は5なので、百の位を0にして、千の位に1を足します。また百の位以下の数はすべて0となるので、3000となります。
2549の十の位を四捨五入してくださいと言われた場合、十の位は4なので、十の位を0にして、十の位以下の数はすべて0となるので、2500となります。
同じ数でも、どの位を四捨五入するかで答えが変わることがあります。また小さな位で四捨五入したほうが「ずれ」は小さくなりますが、計算は大変になります。
小学生の場合、指定された位で四捨五入できればよいですが、実際に社会で使用する際には自分でどの位で四捨五入するか考える必要があります。
(特に理系の場合、有効数字という考え方を身に着ける必要があります。)
[算数の問題]
「1132円は1100円、2549円は2500円、1800円は1800円として計算すると慣れてくれば暗算で、5400円と計算できると思います。」
この文章の計算は、どの位で四捨五入して計算していますか。
(答え)
まず1の位で四捨五入してみてください。1132=>1130、2549=>2550、1800=>1800 となり違うことがわかります。
次に10の位で四捨五入してみます。1132=>1100、2549=>2500、1800=>1800 となり文章と同じ数であることがわかります。
つまり10の位の数で四捨五入しています。
[社会実践問題]
Excel で1132を10の位で四捨五入してください。またGoogle スプレッドシート で1132を10の位で四捨五入してください。
(答え)
大人になるにつれ、知識を増やすことより、知らないことを調べて確認することのほうが重要な能力となります。
検索エンジン、またはAIに聞いてみて、試してみてください。(間違った情報もあるので試してもらえればと思います。)
表計算ソフトやプログラミング言語には、この手の関数が用意されているんだなということを感じてもらえればと思います。
Excel:=ROUND(1132,-2)
Google スプレッドシート:=ROUND(1132,-2)
(3)かけ算(10倍、100倍)
前回1ケタ×10のかけ算は10×1=10、10×5=50、10×9=90 といった感じで位が一つ上がるといった結果となることを説明しました。
では2ケタ×10のかけ算について確認します。
11×10 を計算する場合、10×11 と同じ計算結果となります。
(数の固まり)×(その数の固まりの数)とみると、10が11個あるとみることができます。そのため10が10個で100、それにもう一こ10を追加して、110となります。
34×10 も同様に考えることができ、10が34個あるとみて、340となります。
したがって位が一つ上がって、0が増える結果となります。
次に100をかけたらどうなるかというと、13×100 は 100が13個あるとみることができ、1300 となります。
位が2つあがって、0が2つ増える結果となります。
1000をかけたら、位が3つあがって、0が3つ増える結果となります。
(34 × 1000 = 34000)
10000をかけたら、位が4つあがって、0が4つ増える結果となります。
(71 × 10000 = 710000)
10や100が隠れた計算についても見てみたいと思います。
8 × 90 についてみてみます。
90 = 9×10 と見れるので、8 × 90 = 8×9×10 =72 × 10 =720
次に 8 × 900 についてみてみます。
900 = 9×100 と見れるので、8×900 = 8×9×100 = 72×100 =7200
[算数の問題]
2022円の本を3冊買います。10の位で四捨五入して、大体いくらかかるか計算してください。
(答え)
2022を10の位で四捨五入すると、2000 となります。
2000×3=2×1000×3=6×1000=6000 結果は6000円となります。
(4)かけ算(2桁×1桁、2桁×2桁)
前回、「四角形を1cm×1cmの四角形に分割する」という説明で、以下の図を使って、1cm×1cmの四角形が何個あるか計算しました。
この1cm×1cmの四角形の個数は、多いほど広く、少なくなるとせまくなることがわかると思います。
この広さを面積といいます。
4cm×3cmの四角形で面積を計算すると、「12個の1cm×1cmの四角形」があることがわかります。

この考え方を使って、2ケタ×1ケタの計算を考えてみたいと思います。
〇 2ケタ×1ケタ
48×6 を考えます。この式は、48cm×6cmの四角形の面積を求めることとなります。

図から
(48cm×6cmの四角形の面積)=(40cm×6cmの四角形の面積)+(8cm×6cmの四角形の面積) となることがわかります。
つまり 48×6 =40×6 + 8×6 =4×6×10 + 48=240+48=288 となります。
これは 48を40と8に分け、それぞれに6をかけたあと足していることがわかると思います。
48×6=(40+8)×6=40×6+8×6=240+48=288
逆も成立します。
48×6=(40+8)×6=6×48=6×(40+8)=40×6+8×6
〇 2ケタ×2ケタ
34×58を考えます。
1) 34×58=(30+4)×58=30×58 + 4×58
2) 30×58 と 4×58 をそれぞれ計算します。
30×58=30×(50+8)=30×50+30×8=1500+240=1740
4×58=4×(50+8)=4×50+4×8=200+32=232
3) 1740+232=1972
この計算を1回で書くと以下のように書けます。
34×58=(30+4)×(50×8)=30×50+30×8+4×50+4×8
30に50と8をかけ、4に50と8をかけ、それらをすべて足すことで計算されます。
図形で書くと以下の図のようになります。

数を分解してそれぞれをかけていることがわかると思います。
[算数の問題]
15回コンサートをやって、それぞれのコンサートで53枚チケットが売れました。チケットは全部で何枚売れたでしょうか。
(答え)
(1つのコンサートで売れたチケット数)×(コンサート数)=(すべての売れた枚数)
15 × 53=(10+5)×53
=10×53+5×53=530+5×(50+3)
=530+5×50+5×3=530+250+15=795 答えは795枚です。
(5)わり算とは
わり算について書く前に足し算と引き算の関係について、もう一回確認したいと思います。
〇 足し算と引き算の関係
クッキーが7個あり、A君とB君に分けるとします。その時、
(A君に分けたクッキー)+(B君に分けたクッキー)=(クッキーの全体:7個)
という関係が成立します。
クッキーの全体の数が7個でA君に分けたクッキーが4個だとします。
その場合、(B君に分けたクッキー)=7-4=3 個 となります。
クッキーの全体の数が7個でB君に分けたクッキーが3個だとします。
その場合、(A君に分けたクッキー)=7-3=4 個 となります。
つまり引き算は足し算の相手を求める計算と考えることができます。
〇 かけ算とかけ算の相手を求める計算(=割り算)について
かけ算は(数の固まり)×(その数の固まりの数)と考えることができます。
例えば、1クラスが5人で4クラスあるとき、生徒は全部で何人いるでしょうという問題があったとします。
(1クラスの人数) × (クラス数)=(すべての生徒数) という式が成立します。
そのため、5×4=20 人と計算することができます。
「1クラスの人数」を求めたり、「クラス数」を求めること、つまりかけ算の相手を求める計算をわり算と言います。
(1クラスの人数)は「数の固まり」で、(クラス数)は「その数の固まりの数」となります。
(1クラスの人数)=(すべての生徒数)÷(クラス数)
=20÷4=5 人と計算できます。
20という数を4等分(等しく分ける)していると考えることができるので、難しい言葉で「等分除」といわれます。
(クラス数)=(すべての生徒数)÷(1クラスの人数)=20÷5=4 クラスと計算できます。
20という数には5が何個入っているのかを求める計算と考えることができるので、難しい言葉で「包含除」といわれます。
このようにわり算には2つの意味があります。
計算のコツとして20÷5だったら、5に何をかけたら20になるかを考えることです。そのためかけ算に慣れる必要があります。
また式を立てるコツは、最初からわり算で考えられる場合はよいですが、まずはかけ算の関係性を見つけることを考えてもよいと思います。
かけ算は逆でも計算結果が同じになるので、比較的考えやすいことが多いです。
ひき算のときは「A君のクッキーの数」と「B君のクッキーの数」のように同じ種類のものを求めていました。
しかし、わり算は「1クラスの人数」と「クラス数」のように全然違う種類のものが答えになります。
その答えに対応して計算の意味も2つあります。
これがわり算が難しい理由です。
[算数の問題]
(1)
夏休みの宿題で45問算数の問題を解かなければいけません。1日5問解く場合、何日で終わりますか。
(2)
夏休みが楽しくて宿題を解きわすれ、あと5日間で45問解かないといけません。1日何問解けばよいでしょうか。
(答え)
(1日に解く問題数)×(日数)=(その日数で解く問題数) という関係が成り立ちます。
(1)
1日に解く問題数:5
その日数で解く問題数:45
となるので、5×(日数)=45
(日数)=45÷5=9 9日間で終了します。
(2)
日数:5
その日数で解く問題数:45
となるので、(1日に解く問題数)×5=45
(1日に解く問題数)=45÷5=9 1日で9問解く必要があります。
引き算やわり算は基本的には考えづらいことが多いので、難しいと感じたら足し算やかけ算の関係性を探すようにするとよいと思います。
またつねにきれいにわり算ができるわけではありません。その場合、なるべく大きな数を考えて残りを「あまり」として求めることがあります。
[算数の問題]
9個のチョコレートを持っています。4人の子供に同じ数あげるとき、一人何個あげることができますか。また何個あまりますか。
(答え)
(1人にあげる数)×(子供の人数)=(チョコレートの数) で考えます。
(1人にあげる数)×4=9 となりますので、9÷4 を計算することになります。
4×2=8、4×3=12 なので2個まではあげれそうです。さらに9-8=1 で1個あまります。
つまり1人にあげれる個数は2個、あまりは1個が答えとなります。
(6)分数
〇 新しい数=分数
ホールケーキを3人で分けるとします。その時1,2,3のようなきれいな数では表せませんが、確かに3人できれいに分けることができます。
色のついた部分が一人分です。

この3つで1になるような半端な数を分数といい、$${\frac{1}{3}}$$のように表します。
5つで2になるような半端な数は$${\frac{2}{5}}$$となります。
この時の横棒の上の数を分子、下の数を分母と呼びます。
〇 分数と割り算
ホールケーキを3人で分けるとき、1人分を計算すると、1つのものを3つに等分するので、1÷3で計算することとなります。
そして一人分は$${\frac{1}{3}}$$となるので、1÷3=$${\frac{1}{3}}$$ となります。
〇÷△=$${\frac{〇}{△}}$$ と表現することができます。
「△分の〇」と言います。
また分数で表す場合、「あまり」は無くなります。例を見てみます。
「9個のチョコレートを持っています。4人の子供に同じ数あげるとき、一人何個あげることができますか。」という問いを考えてみます。
(1人にあげる数)=9÷4 で計算できるので、$${\frac{9}{4}}$$となります。一つを4分割して、それの9つ分を赤、黄、緑、青と色分けしています。

赤、黄、緑、青をそれぞれ一人と考えると、同じ量食べることができます。分数という新しい数を入れることで、一つもあまらせることなく正確に分けることができました。
〇 1の分数表現と、分母が1の分数
1も分数で表すことができます。
例えば、4つのクッキーを4人で分けました。1人分のクッキーの枚数を求めると、4÷4=1 となりますが、分数で書くと4÷4=$${\frac{4}{4}}$$ となります。
1つのクッキーを1人で分ける場合、5つのクッキーを5人で分ける場合等、
〇÷〇=$${\frac{〇}{〇}}$$ が1となることがわかります。分子と分母が同じ数の時に1となります。
次に、2,3,4,5といったこれまで使ってきた数が分数で表せるか考えてみたいと思います。
2つのクッキーを1人で食べました。何枚食べれましたかといわれたら、
2÷1=2 で計算でき、分数で書くと2÷1=$${\frac{2}{1}}$$となります。
このように2,3,4,5といった数も分母を1、分子を2,3,4,5とすることで表現することができます。
最後に0についてですが、0個のクッキーを100人で食べました。一人が食べれる数を求めると、0÷100=0 分数で書くと0÷100=$${\frac{0}{100}}$$となります。このように0は分子が0であれば表現することができます。
つまり、0,1,2,3…といったこれまで習った数は分数で表すことができます。分数というものはこれまで習った数より大きい考え方であることがわかります。
さて小学校の範囲を超え、高校数学の範囲ですが、10個のクッキーを0人で食べました。一人が食べれる数を考えるとします。計算式は10÷0です。
例えば、10個のクッキーを10人でたべると、1人で食べれる量は10÷10=$${\frac{10}{10}}$$=1となります。
1人で食べると10÷1=$${\frac{10}{1}}$$=10 となり、分母が減るほど答えの数が増えることがわかると思います。
同じ数を分ける人が減れば、一人が食べれる数は増えます。10÷0は最も分ける人数が少ない数で、とんでもない数となります。この数は数字で表すことができず、無限大(∞)と表します。
小学校~中学校の範囲ではこれを考える意味がないです。そのため問題に出すべきではないと思いますが、もし出たら先生の言っていた通りに書いてください。
〇 分数は同じ数でもいろいろな表現ができる。
以下の図を見てください。左は3つに分けており、右は6つに分けています。そして色を塗った部分は同じです。そのため3つに分けたものの一つ分は、6つに分けたものの2つ分になることがわかります。

「6つに分けたものの2つ分」は、6つあれば2つになります。
(この色のついた部分が3つあれば1つになるので、6つあれば2つになります。)
つまり6つあれば2つになる数なので、$${\frac{2}{6}}$$となります。
または6等分されている$${\frac{1}{6}}$$が2つあるので、$${\frac{2}{6}}$$と考えてもよいです。
この$${\frac{2}{6}}$$は$${\frac{1}{3}}$$と同じ色を塗った部分を表しているということがわかります。
今は分子と分母に同じ数をかけたり、同じ数で割った数は同じ数になると考えておいてください。
$${\frac{1}{3}}$$の分子と分母に2をかけると、$${\frac{2}{6}}$$となります。
$${\frac{2}{6}}$$の分子と分母を2でわると、$${\frac{1}{3}}$$となります。
最も少ない数で表すための計算方法については、もう少し後で勉強します。
[算数の問題]
(1)
次の数のうち、1より大きい数を答えてください。(1は含みません)
$${\frac{5}{1}}$$、$${\frac{6}{3}}$$、$${\frac{4}{4}}$$
(2)
以下の点Aを分数で表してください。

(答え)
(1)
$${\frac{5}{1}}$$は分母が1なので5となり、1より大きいことがわかります。
$${\frac{6}{3}}$$=6÷3=2 なので、1より大きい数であることがわかります。
$${\frac{4}{4}}$$は分子、分母が同じ数なので1となり、1より大きい数ではありません。
(2)
0から1で5分割されていることがわかります。つまり1目盛りは5個で1になる数、つまり$${\frac{1}{5}}$$になることがわかります。
そして点Aは目盛り3つ分なので、$${\frac{3}{5}}$$となります。
(7)小数
$${\frac{1}{10}}$$ や $${\frac{1}{100}}$$ が何個分というときは、「.」を使って数を表すことができ、これを小数と言います。
$${\frac{1}{10}}$$は「0.1」、$${\frac{1}{100}}$$は「0.01」と表します。
例えば$${\frac{5}{10}}$$は「0.5」、$${\frac{8}{100}}$$は「0.08」と表すことができます。
さらに、$${\frac{1}{10}}$$が10個あれば1なので、$${\frac{17}{10}}$$は1と$${\frac{7}{10}}$$となり、「1.7」と表現することができます。
なぜ$${\frac{1}{10}}$$ や $${\frac{1}{100}}$$だけ特別に小数で表せるかというと、0から9までの数で位が上がるからです。
「0.1」から0.1増えると「0.2」となり、同じように「0.3」「0.4」となり、「0.9」の次は「1.0」となります。
同じように「0.01」から0.01増えると「0.02」となり、同じように「0.03」「0.04」となり、「0.09」の次は「0.1」となります。
このように0から9まで増えていき、さらに増えると位が上がるという特徴があるので、これまでは左側に位を作ってきたのですが、「.」を使って右側に位を作ったのが小数ということになります。
[算数の問題]
(1)
10分の3を小数と分数で表してください。
(2)
黄色の棒の長さを分数と小数で表してください。(0cmのところと黄色の棒の先はくっついています。)

(3)
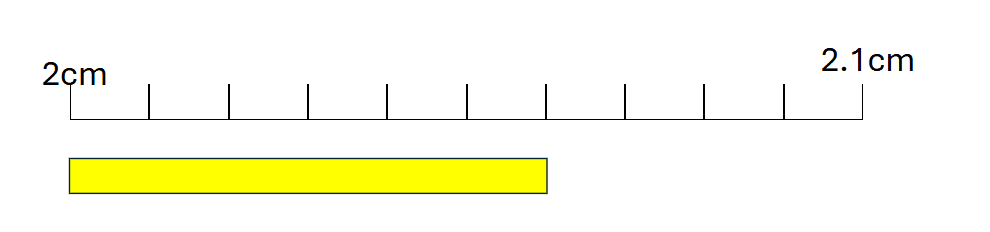
黄色の棒の長さを分数と小数で表してください。(0cmのところと黄色の棒の先はくっついています。)
(答え)
(1)
$${\frac{3}{10}}$$=0.3
(2)
1から2の間が10分割されているので、1目盛りは$${\frac{1}{10}}$$cmを表します。0から1cmまでで、目盛りは10個あり、さらに1cmから2cmの間で7個あります。$${\frac{1}{10}}$$が17個あるので、$${\frac{17}{10}}$$cmと表せます。
さらに$${\frac{17}{10}}$$を小数で表すと1.7cmとなります。
(3)
2から2.1の間が10分割されているので、1目盛りは$${\frac{1}{100}}$$cmを表します。0から2cmまでで、目盛りは200個あり、さらに2cmから2.1cmの間で6個あります。$${\frac{1}{100}}$$が206個あるので、
$${\frac{206}{100}}$$cmと表せます。
さらに$${\frac{206}{100}}$$を小数で表すと2.06cmとなります。
(8)おまけ:分離量と連続量
世の中には分離量と連続量というものがあります。分離量は「数えれる量」のことで、例としては卵の数とか、クッキーの数があります。
連続量は「測る量」のことで、例としては棒の長さや水の量があります。
分数を扱う場合、連続量にすると扱いやすくなることがあります。
[社会実践問題]
3つのリンゴを5人の子供に同じ量だけあげたいときどうすればよいでしょうか。
(答え)
上手く一つのリンゴを5分割できる人ならよいかもしれませんが、難しいと思います。そこでリンゴジュースにすると、5個のコップを用意して、すこしづつ分けると上手く5人に分けることができるでしょう。
「リンゴ」という分離量を「リンゴジュース」という連続量にすることで分けやすくなるという例です。
私の個人的な経験だと小学校3-4年生の算数は難しかったと思います。
計算が難しいことよりも概念を広げることのほうが難しかったんだと思います。
わり算には2つの意味があります。さらにその答えとして、分数や小数が生まれ、さらにその分数は1,2,3といった馴染みのある数を含む広い概念であることを理解する必要があります。
わり算の説明の際には、「わる数」と「わられる数」といった私にはうまく理解できない説明がされます。わり算について理解するためには、方程式まで学ぶ必要があったと感じています。
そこでかけ算で考えるという方法で説明してみました。私の中ではこのほうが頭から出し入れしやすいので、試してみてもらえると嬉しいです。
この記事が気に入ったらサポートをしてみませんか?
