数学オリンピックでハイスコアのAIから考えるAIと人の住み分け
0.はじめに
私は生成AIに関しては、ベーシックインカムの実現を考えないといけないほどのものにならないなら不要派です。(画像認識の一部の技術については現時点でも有用だと思っています。)
雇う人を5人から3人にします程度の発展が一番厄介だとおもっています。
また電気は当然、水もかなり食うため本当に使用価値があるものになってほしいと思っています。
(今後油冷などでもう少し改善するのかもしれませんが。)
以下の記事を見かけて、AIの現在地点を知りたいと思っていろいろ調べてみました。
Google DeepMind が開発した AlphaProof は2つの代数問題と1つの数論問題で満点を獲得。また、AlphaGeometry 2が幾何学の問題で満点を獲得し、合計得点は28点となりました。2024年の国際数学オリンピックでは金メダルのラインが29点であり、惜しくも金メダル獲得とはなりませんでした。
実際の出力内容が欲しかったので以下のリンクからダウンロードしました。
またLean ファイルの読み込みについては以下を参照しました。
Lean ファイルの解答例(P1)は以下の通りです。実際に動かせなかったことや、どこまでが手作業かの境界が分かりづらかったので、多分こうだろうという想像はあるのですが、正確な評価はできていないです。
import Mathlib.Algebra.EuclideanDomain.Basic
import Mathlib.Algebra.EuclideanDomain.Int
import Mathlib.Analysis.RCLike.Basic
import Mathlib.Tactic.Have
open scoped BigOperators
/--
Determine all real numbers $\alpha$ such that, for every positive integer $n$, the integer
$$
\lfloor \alpha\rfloor + \lfloor2\alpha\rfloor + \cdots + \lfloor n\alpha\rfloor
$$
is a multiple of $n$.
(Note that $\lfloor z\rfloor$ denotes the greatest integer less than or equal to $z$.
For example, $\lfloor-\pi\rfloor = -4$ and $\lfloor2\rfloor = \lfloor2.9\rfloor = 2$.)
Solution: $\alpha$ is an even integer.
-/
theorem imo_2024_p1 :
{(α : ℝ) | ∀ (n : ℕ), 0 < n → (n : ℤ) ∣ (∑ i in Finset.Icc 1 n, ⌊i * α⌋)}
= {α : ℝ | ∃ k : ℤ, Even k ∧ α = k} := by
rw [(Set.Subset.antisymm_iff ), (Set.subset_def), ]
/- We introduce a variable that will be used
in the second part of the proof (the hard direction),
namely the integer `l` such that `2l = ⌊α⌋ + ⌊2α⌋`
(this comes from the given divisibility condition with `n = 2`). -/
existsλx L=>(L 2 two_pos).rec λl Y=>?_
useλy . x=>y.rec λS p=>?_
· /- We start by showing that every `α` of the form `2k` works.
In this case, the sum simplifies to `kn(n+1)`),
which is clearly divisible by `n`. -/
simp_all[λL:ℕ=>(by norm_num[Int.floor_eq_iff]:⌊(L:ℝ)*S⌋=L* S )]
rw[p.2,Int.dvd_iff_emod_eq_zero,Nat.lt_iff_add_one_le,<-Finset.sum_mul,←Nat.cast_sum, S.even_iff, ←Nat.Ico_succ_right,@ .((( Finset.sum_Ico_eq_sum_range))),Finset.sum_add_distrib ]at*
simp_all[Finset.sum_range_id]
exact dvd_trans ⟨2+((_:ℕ)-1),by linarith[((‹ℕ›:Int)*(‹Nat›-1)).ediv_mul_cancel$ Int.prime_two.dvd_mul.2<|by ·omega]⟩ ↑↑(mul_dvd_mul_left @_ (p))
/- Now let's prove the converse, i.e. that every `α` in the LHS
is an even integer. We claim for all such `α` and `n ∈ ℕ`, we have
`⌊(n+1)*α⌋ = ⌊α⌋+2n(l-⌊α⌋)`. -/
suffices : ∀ (n : ℕ),⌊(n+1)*x⌋ =⌊ x⌋+2 * ↑ (n : ℕ) * (l-(⌊(x)⌋))
· /- Let's assume for now that the claim is true,
and see how this is enough to finish our proof. -/
zify[mul_comm,Int.floor_eq_iff] at this
-- We'll show that `α = 2(l-⌊α⌋)`, which is obviously even.
use(l-⌊x⌋)*2
norm_num
-- To do so, it suffices to show `α ≤ 2(l-⌊α⌋)` and `α ≥ 2(l-⌊α⌋)`.
apply@le_antisymm
/- To prove the first inequality, notice that if `α > 2(l-⌊α⌋)` then
there exists an integer `N > 0` such that `N ≥ 1/(α - 2(l -⌊α⌋))`.
By our assumed claim (with `n = N`), we have
`⌊α⌋ + 2(l-⌊α⌋)N + 1 > (N+1)α`, i.e.
`⌊α⌋ + (2(l-⌊α⌋) - α)N + 1 > α`,
and this implies `⌊α⌋ > α`; contradiction. -/
use not_lt.1 (by cases exists_nat_ge (1/(x-_)) with|_ N =>nlinarith[ one_div_mul_cancel $ sub_ne_zero.2 ·.ne',9,Int.floor_le x, this N])
/- Similarly, if `α < 2(l-⌊α⌋)` then we can find a positive natural `N`
such that `N ≥ 1/(2(l-⌊α⌋) - α)`.
By our claim (with `n = N`), we have
`(N+1)α ≥ ⌊α⌋ + 2(l-⌊α⌋)N`, i.e.
`α ≥ ⌊α⌋ + (2(l-⌊α⌋) - α)N`,
and this implies `a ≥ ⌊α⌋ + 1`; contradiction. -/
use not_lt.1 (by cases exists_nat_ge (1/_:ℝ)with|_ A=>nlinarith[Int.lt_floor_add_one x,one_div_mul_cancel$ sub_ne_zero.2 ·.ne',this A])
/- Now all that's left to do is to prove our claim
`⌊(n + 1)α⌋ = ⌊α⌋ + 2n(l - ⌊α⌋)`. -/
intro
-- We argue by strong induction on `n`.
induction‹_› using@Nat.strongInductionOn
-- By our hypothesis on `α`, we know that `(n+1) | ∑_{i=1}^(n+1) ⌊iα⌋`
specialize L$ ‹_›+1
simp_all[add_comm,mul_assoc,Int.floor_eq_iff,<-Nat.Ico_succ_right, add_mul,(Finset.range_succ), Finset.sum_Ico_eq_sum_range]
revert‹ℕ›
/- Thus, there exists `c` such that
`(n+1)*c = ∑_{i=1}^{n+1} ⌊iα⌋ = ⌊nα+α⌋ + ∑_{i=1}^n ⌊iα⌋`. -/
rintro A B@c
simp_all[ Finset.mem_range.mp _,←eq_sub_iff_add_eq',Int.floor_eq_iff]
/- By the inductive hypothesis,
`∑_{i=0}^{n-1}, ⌊α+iα⌋ = ∑_{i=0}^{n-1}, ⌊α⌋+2*i*(l-⌊α⌋)`. -/
suffices:∑d in .range A,⌊x+d*x⌋=∑Q in .range A,(⌊x⌋+2*(Q * (l-.floor x)))
· suffices:∑d in ( .range A),(((d)):ℤ) =A * ( A-1)/2
· have:(A : ℤ) * (A-1)%2=0
· cases@Int.emod_two_eq A with|_ B=>norm_num[B,Int.sub_emod,Int.mul_emod]
norm_num at*
norm_num[ Finset.sum_add_distrib,<-Finset.sum_mul, ←Finset.mul_sum _ _] at*
rw[eq_sub_iff_add_eq]at*
/- Combined with
`∑_{i=0}^{n-1},⌊iα+α⌋ = (n+1)c - ⌊nα+α⌋`,
we have `⌊nα+α⌋ = (n+1)c - n⌊α⌋ - n(n-1)(l-⌊α⌋)`, so
`⌊nα+α⌋ ≥ (n+1)c - n⌊α⌋ - n(n-1)(l-⌊α⌋)`
and
`⌊nα+α⌋ < (n+1)c - n⌊α⌋ - n(n-1)(l-⌊α⌋) + 1`.
Also, since `2*l = ⌊α⌋ + ⌊2α⌋`, we have
`2α+⌊α⌋-1 < 2*l ≤ 2α+⌊α⌋.`-/
zify[←mul_assoc, this,←eq_sub_iff_add_eq',‹_ =(@ _) /@_›,Int.floor_eq_iff] at *
zify[*]at*
-- We will now show that `c = n*(l-⌊α⌋) + ⌊α⌋`.
cases S5:lt_or_ge c (A * (l-.floor ↑x)+⌊x⌋ + 1)
· simp_all
have:(c+1:ℝ)<=A*(l-⌊x⌋)+⌊x⌋+1:=by norm_cast
simp_all
cases this.eq_or_lt
· /- For if `c = n*(l-⌊α⌋) + ⌊α⌋`, then
```
⌊(n+1)α⌋ = (n+1)c - n⌊α⌋ - n(n-1)(l-⌊α⌋)
= (n+1)(n(l - ⌊α⌋) + ⌊α⌋) - n⌊α⌋ - n(n-1)(l-⌊α⌋)
= 2n(l-⌊α⌋) + ⌊α⌋
```
as desired. -/
repeat use by nlinarith
/- Now, we show `c = n*(l-⌊α⌋) + ⌊α⌋` via contradiction
split into two cases. First suppose `c ≤ n(l - ⌊α⌋) + ⌊α⌋ - 1`.
```
(n+1)α < (n+1)c - n⌊α⌋ - n(n-1)(l-⌊α⌋) + 1
≤ (n+1)(n(l-⌊α⌋) + ⌊α⌋ - 1) - n⌊α⌋ - n(n-1)(l-⌊α⌋) + 1
= 2n(l-⌊α⌋) + ⌊α⌋ - n
= 2ln - 2n⌊α⌋ + ⌊α⌋ - n
≤ (2α+⌊α⌋)n - 2n⌊α⌋ + ⌊α⌋ - n
= nα + n(α-⌊α⌋-1) + ⌊α⌋
n + α.
```
contradiction. -/
nlinarith[(by norm_cast at* :(A*(l -⌊x⌋):ℝ)+⌊(x)⌋ >=(c)+01),9,Int.add_emod ↑5,Int.floor_le (@x : ℝ),Int.lt_floor_add_one (x:)]
/- Next, suppose `c ≥ n(l - ⌊α⌋) + ⌊α⌋ + 1`.
```
(n+1)α ≥ (n+1)c - n⌊α⌋ - n(n-1)(l-⌊α⌋)
≥ (n+1)(n(l-⌊α⌋) + ⌊α⌋ + 1) - n⌊α⌋ - n(n-1)(l-⌊α⌋)
= 2n(l-⌊α⌋) + ⌊α⌋ + n + 1
= 2ln - 2n⌊α⌋ + ⌊α⌋ + n + 1
> (2α+⌊α⌋-1)n - 2n⌊α⌋ + ⌊α⌋ + n + 1
= nα + n(α-⌊α⌋) + ⌊α⌋ + 1
> n + α
```
contradiction. -/
simp_all
nlinarith[(by norm_cast:(c:ℝ)>=A*(l-⌊_⌋)+⌊_⌋+1),Int.floor_le x,Int.lt_floor_add_one x]
rw [←Nat.cast_sum, mul_sub, Finset.sum_range_id]
cases A with|_=>norm_num[mul_add]
use Finset.sum_congr rfl<|by simp_all[add_comm,Int.floor_eq_iff]
#print axioms imo_2024_p1
1.問題と解答について得た感覚
同様の内容について別記事を見つけたのでそちらも確認しました。
「AlphaProofは代数の問題2つと数論の問題1つを解いた。そのうちの1つはIMOで最高難易度の問題だった。AlphaGeometry 2は幾何学の問題を1つ解いたが、組み合わせ論(集計と物体の配置を扱う数学分野)の問題2つは未回答だった。」
問題は以下のサイトを参考にしました。
回答は以下のサイトを参照しました。
問題1

答え:αは整数であり、偶数
AlphaProofが回答したものとしてLeanファイルが存在しました。私は専門家ではないのですが、解くために導入した変数に関しては少し人が思いつきづらいアプローチなのかなと感じました。
問題2

答え:(a,b)=(1,1)のみ
AlphaProofが回答したものとしてLeanファイルが存在しました。オイラーの定理を使ったり、解法は一般的に見えました。
問題3
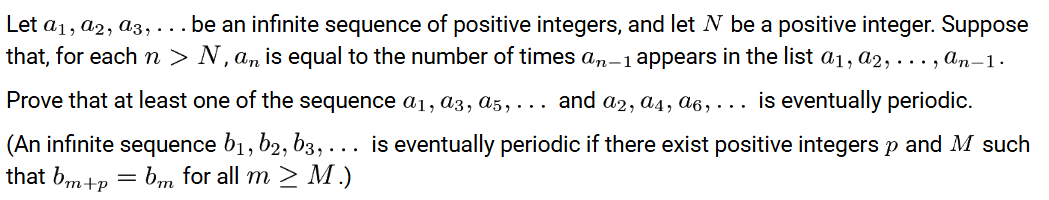
AlphaProofは解けていませんでした。数列(?)の問題で方針が立たなかったのかなと思いました。
問題4

AlphaGeometry 2で解いた問題だと思われます。補助線を引いたと思いますが、総当たりで引いて、辻褄が合うか考えればばよいと考えるとチェスに近いかもしれないなと感じました。補助線はひらめきと思っていましたが、いろいろなパターンを飽きずにやれる人がいるなら確かに計算量の問題と言えると思いました。
問題5

AlphaProofは解けていませんでした。ゲームのルールが把握できなかった、またはいろいろ検証してみて規則性を見つけるみたいな処理が苦手なのかもしれません。
問題6

答え:c=2
AlphaProofが回答したものとしてLeanファイルが存在しました。ちょっとこの問題は自分の英語の問題の理解や回答の理解が不十分なところがあり、感触がえられなかったです。
2.自分の勝手な感想
何がやれて何がやれないのか知りたくていろいろ見ましたが、まずは「ひらめき」というものについて考えさせられました。
補助線の問題は「ひらめき」だと思っていましたが、高校数学までに限定したとき補助線の引き方にはある程度上限があり、そのパターンを各頂点に対して片っ端から実行するとかんがえると、計算量の問題だなとはっとしました。
ただ例えば原子が蛇のようにうねっており、さらに1匹の蛇が自身の尻尾に噛み付きながら回っている夢を見て、ベンゼンの環状構造を思いついた(ケクレの夢)のようなことは依然として「ひらめき」と呼んでいいものだと思います。「ひらめき」とは脳の中でいろいろな分野のイメージが混ざり、自分の考えている課題を解決することという狭い定義になるかもしれません。
次に問題に出会ってから解くまでの過程でAIと人の得意領域を考えてみました。
①「問題設定」:意欲(解きたい、若しくはこれを問題と設定する)は人の領域だと思います。AIに勝手に決めて解かれても、リソースが無尽蔵ということもないと思うので、要らないと判断されることがほとんどだと思います。
②「問題解釈」:問題を解釈してその分野が得意なAIに渡してやる必要がありそうだなと感じています。それもAIで設定できそうですが、例えば経済の問題を数学の問題に書き換える等は人がやらないとその人が欲しい回答が得られないのではと感じています。
➂「解く」:ジャンルと武器を設定されればできそうだなと感じました。現時点で、例えば「幾何の問題を座標問題にしたり、ベクトルにして解く案を提案できるか」といったことは気になります。
広い範囲を学習させると精度が下がっていきそうなので、解き方も人が決めて得意なAIに任せるといった流れになるのではと感じました。
また現時点では自分で実験して結果から法則を見つけるみたいなことが苦手なのではと感じています。(よく数列などである問題です。)この感覚が正しいか検証してみたいですが、数学の中でも得意と不得意がある場合、かなり使いづらいものになりそうだと思います。
④「回答吟味」:出来ていないときは回答を出さないようにしてほしいなと思います。難しいものになると合っているかの確認に時間がかかるからです。今回の未回答がそれに当たるなら良い機能だと思います。
また②で言ったように経済を数学の問題に読み替えて解いてもらった場合は、再度答えを経済に変換する必要があるので、ここも人の仕事になるかなと思います。
ここまでの論がある程度正しいとすると、やる気と基礎的な学力があり、ジャンルを超える力を育成することが教育であり、教えるべき内容とかは実はそこまで変わらないのではと思いました。
ただこれまでみたいに解法暗記して解くみたいな能力がそこまで必要ではなく、基礎的な能力と解答を追える力を育成することがメインになるかなと思います。
また分野を超えることはAIにとって難しいのではと思いました。
広い知性を持ったAIは精度が悪く使いづらいものになるのではないかなと思います。
(現在のChatGptの後ろ側にAlphaProofなどの数学系AIや、GithubCopilotなどのプログラミング系AIを配置して質問するより、それぞれを使い分けたほうがまだ使いやすいと感じるのではと思います。)
そう考えると人に関しては「広く全体を知ることで分野を超えることができる」可能性にかけ全体的な基礎力を構築するのが教育のメインテーマになるかなと思いました。
またよくAIは計算機とかと一緒で道具という人がいますが、入力に対して出力が同じではなくまたどうしてその結論が出たか追いにくいので、答えがある業界(数学-答えがでない,プログラミング-動かない等)では計算機ほどの能力を発しないものと感じています。
計算機能がなくなったら困りますが、現在の生成AI系のツールを使えなくてもそこまで困らないと思います。
例えば今のようなサービス価格でなくAIの使用にがっつりコストがかかるようになればもういいかなと思う人も出てくると思います。
画像認識におけるディープラーニングはかなり機能していると感じました。生成AIのジャンルに関しては、ハード面も理論面も何か超えないといけない大きな隔たりがあるのではないかと感じました。
もう少し実物を触れそうな機会ができてから、もう一度検証してみたいと思います。
この記事が気に入ったらサポートをしてみませんか?
