【対象年齢：小３〜】ある虫食い算について考えてみたら面白かったので共有したい

この記事は、日曜数学 Advent Calendar の11日目の記事です。

adventar.org

0.はじめに

普段は小学校で子どもたちと算数を楽しんでいます。それでは日曜数学の趣旨に反するのではないかと思い、tsujimotterさんに確認を取ったところ、ご快諾いただけたので、今回の記事を投稿します。

1.虫食い算とは

今回の記事では、虫食い算について話します。

虫食い算（むしくいざん、英: cryptarithm, 英: arithmetical restorations[1], 英: digital puzzle, 英: restoration problem, 英: missing figure puzzle, 英: dotty puzzle[2]）は、いくつかの数字が伏せられた計算式を与えられ、明らかになっている部分から伏せられた数字が何であるかを推理し、完全な計算式を導き出すパズルである。解き手のヒントになるように、計算式は筆算の形で与えられることが多い。

虫食い算−Wikipedia

例えば、次の計算で□に当てはまる整数（0~9）を求める問題を考えます。

$$
\begin{array}{rrrr}
&1 & □ & 3\\
+& & 4 & □\\
\hline
& 1 & 6 & 8
\end{array}
$$

一の位を見ると、$${3+□=8}$$となっているので、$${□=5}$$です。
同じように十の位を見ると、$${□+4=6}$$となっているので、$${□=2}$$です。ここで気をつけることは、一の位でくり上がりが起きていないということ。もし一の位でくり上がりがあると、$${□=1}$$になります。

2.今回の問題

問題：次の$${□}$$に1~9の整数を1つずつ入れて、式を完成させましょう。

$$
\begin{array}{rrrl}
&□ &□ &□\\
+&□ & □ & □\\
\hline
& □ &□ &□\\
\end{array}
$$

面白い問題なので、ぜひ考えてみてください。

小学生にこの問題を出すと、勘の良い子は「先生、この問題答え1つじゃないでしょ？」などと言ってきます。「さあ、どうかな？」とはぐらかしていると、子どもたちは思い思いに数を入れて計算を始めます。

そのうち、答えが出る子が出てくるわけですが、「先生、やっぱり答え1つじゃない！」と言う声が上がってきます。

実際、この問題の答えは100通り以上あります。そのうちのいくつかを書いてみると、

$$
\begin{array}{rrrl}
&4 & 2 & 9\\
+& 1& 3 & 8\\
\hline
& 5 & 6 &7
\end{array}
$$

$$
\begin{array}{rrrl}
&4 & 9 &2\\
+& 1& 8 & 3\\
\hline
& 6 & 7 &5
\end{array}
$$

$$
\begin{array}{rrrl}
&7 & 5 & 2\\
+& 1& 8 & 4\\
\hline
& 9 & 3 &6
\end{array}
$$

$$
\begin{array}{rrrl}
&1 & 7 & 3\\
+& 2& 8 & 6\\
\hline
& 4 & 5 &9
\end{array}
$$

というように、いっぱいあります。
はじめの2つは、位ごとに上手く数を入れ替えた形になっていますね。

「子どもたちが一生懸命計算して、各々が異なる正しい答えを得ることができる。」

これだけで十分面白いのですが、せっかくなので、問題を拡張します。

さっきの問題は1~9を1つずつだったので、0を使えるようにしてみます。
すると、$${□}$$の数が足りなくなる。ここが肝になります。

3.今回の問題：改題

問題：次の$${□}$$に0~9の整数を1つずつ入れて、式を完成させましょう。ただし、0~9のうち、どれか1つの整数は使いません。

$$
\begin{array}{rlrl}
&□.&□&□\\
+&□.&□&□\\
\hline
& □.&□&□\\
\end{array}
$$

小数点をつけているのは、最高位に0を入れられるようにするためです。

この問題、当然ながら、さっきの問題の答えをそのまま使うこともできます（0ナシのパターン）。
それではつまらないので、ここでは0ナシ以外を考えることにしました。

まず浮かぶ疑問は、
・1ナシ、2ナシ・・・、9ナシまで、全てのパターンで解があるのか？
・答えに何か法則性はあるのか？
・もし法則性があるとしたら、どうしてなのか？
といったことです。

実際に確かめてみましょう。
自分で考えたい方は、ここでスワイプを止めてください。

1ナシの場合

$$
\begin{array}{rlrl}
&2.&5&8\\
+&3.&4&9\\
\hline
& 6.&0&7\\
\end{array}
$$

$$
\begin{array}{rlrl}
&0.&8&5\\
+&2.&7&9\\
\hline
& 3.&6&4\\
\end{array}
$$

2ナシの場合

$$
\begin{array}{rlrl}
&3.&6&7\\
+&0.&9&1\\
\hline
& 4.&5&8\\
\end{array}
$$

$$
\begin{array}{rlrl}
&0.&9&7\\
+&5.&4&1\\
\hline
& 6.&3&8\\
\end{array}
$$

3ナシの場合

$$
\begin{array}{rlrl}
&1.&2&5\\
+&6.&7&9\\
\hline
& 8.&0&4\\
\end{array}
$$

$$
\begin{array}{rlrl}
&0.&5&9\\
+&1.&8&7\\
\hline
& 2.&4&6\\
\end{array}
$$

4ナシの場合

$$
\begin{array}{rlrl}
&1.&9&5\\
+&0.&7&3\\
\hline
& 2.&6&8\\
\end{array}
$$

$$
\begin{array}{rlrl}
&2.&7&6\\
+&1.&0&9\\
\hline
& 3.&8&5\\
\end{array}
$$

5ナシの場合

$$
\begin{array}{rlrl}
&6.&8&2\\
+&0.&4&9\\
\hline
& 7.&3&1\\
\end{array}
$$

$$
\begin{array}{rlrl}
&1.&7&9\\
+&6.&2&4\\
\hline
& 8.&0&3\\
\end{array}
$$

6ナシの場合

$$
\begin{array}{rlrl}
&0.&8&1\\
+&4.&9&2\\
\hline
& 5.&7&3\\
\end{array}
$$

$$
\begin{array}{rlrl}
&2.&7&6\\
+&1.&0&9\\
\hline
& 3.&8&5\\
\end{array}
$$

7ナシの場合

$$
\begin{array}{rlrl}
&1.&4&6\\
+&0.&8&9\\
\hline
& 2.&3&5\\
\end{array}
$$

$$
\begin{array}{rlrl}
&6.&4&3\\
+&2.&5&8\\
\hline
& 9.&0&1\\
\end{array}
$$

8ナシの場合

$$
\begin{array}{rlrl}
&1.&9&3\\
+&0.&6&4\\
\hline
& 2.&5&7\\
\end{array}
$$

$$
\begin{array}{rlrl}
&2.&3&4\\
+&6.&7&1\\
\hline
& 9.&0&5\\
\end{array}
$$

9ナシの場合

$$
\begin{array}{rlrl}
&0.&8&4\\
+&2.&6&7\\
\hline
& 3.&5&1\\
\end{array}
$$

$$
\begin{array}{rlrl}
&4.&7&5\\
+&1.&2&8\\
\hline
& 6.&0&3\\
\end{array}
$$

ということで、全てのパターンで解があることがわかりました。

4.改題の答えにきまりはあるか？

次に気になるのは、この答えにきまりはあるのか？ということです。

実際の教室ではきまりに気が付いた子が僅かながらいて、その子からヒントを出してもらう形で、多くの子がきまりに気がつくことができました。
そのヒントは「答えを細かく見る」です。
簡単すぎず、かと言って難しすぎず、絶妙なヒントでした。

4-1:1つ目のきまり

「各パターンで、答えの各位の和が等しい」

これが1つ目のきまりです。

例えば最後の9ナシの場合だと、
　$${0.84+2.67=3.51}$$　→　$${3+5+1=9}$$
　$${4.75+1.28=6.03}$$　→　$${6+0+3=9}$$
のように、答えの各位の和は常に9になります。

この目で元々の問題を見てみると、0ナシの場合にも
　$${4.29+1.38=5.67}$$　→　$${5+6+7=18}$$
　$${7.52+1.84=9.36}$$　→　$${9+3+6=18}$$
　$${1.73+2.86=4.59}$$　→　$${4+5+9=18}$$
のように、答えの各位の和は常に18になっていました。

伏線回収、成功です。

4-2:2つ目のきまり

さて、各パターンで答えの各位の和が等しいことがわかりました。
せっかくなので、表にしてまとめてみます。

こうして見ると、2つ目のきまりが見えてきます。

「◯ナシの偶奇ごとに、答えの各位の和は1ずつ減る」

偶数ナシでは、18、17、16、15、14と1ずつ減っている

奇数ナシでは、13、12、11、10、9と1ずつ減っている

突然の偶奇性。不思議ですよね。
授業はこのきまりを見つけたところで終了していますが、ここでは、この理由について考えてみます。

5.きまりの理由を考える

ポイントは2つです。
　1つ目：くり上がりの回数
　2つ目：「筆算の上側6つの数の和」と「下側(答え)3つの数の和」の関係

5-1:くり上がりの回数

「偶数ナシの場合には、くり上がりの回数は必ず1回になる。」
このことを示していきます。

元々使えた数は0~9の10個で、偶数も奇数も5個ずつです。
ここから偶数を1つナシにするので、偶数4個、奇数5個の9個を使います。

ここで、足し算と偶奇性について確認します。
当たり前のことですが、
　①偶数＋偶数＝偶数　（偶数3個、奇数0個）
　②偶数＋奇数＝奇数　（偶数1個、奇数2個）
　③奇数＋奇数＝偶数　（偶数1個、奇数2個）
です。

今回の問題は3桁の足し算なので、足し算の計算は3回あります。
しかし、①〜③の式を重複を許して3つ組み合わせたところで、偶数4個と奇数5個をぴったり使い切ることはできません。

そこで、私たちには「くり上がり」という「裏技」があります。
見た目上は① 偶数＋偶数であっても、前の位から「くり上がり」があれば、①' 偶数＋偶数＋１＝奇数のように、答えは奇数になります。

先の3式にくり上がりを加味すれば、次の3式を得ることができます。
　①' 偶数＋偶数＋１＝奇数　（偶数2個、奇数1個）
　②' 偶数＋奇数＋１＝偶数　（偶数2個、奇数1個）
　③' 奇数＋奇数＋１＝奇数　（偶数0個、奇数3個）

①〜③、①' 〜③'の6式を上手く組み合わせて、偶数4個と奇数5個をぴったり使い切ることを考えると、くり上がりの回数はちょうど1回でないといけません。

くり上がりの回数が3回でも大丈夫そうに思えますが、最高位の足し算がくり上がってしまうと答えが4桁になってしまうので、上手くいきません。

同じように、次のことが示せます。

「奇数ナシの場合には、くり上がりの回数は必ず2回になる。」

くり上がりの回数が0回でも大丈夫そうに思えますが、その場合は0を使えるマスがなくなってしまいます。

よって、偶数ナシの場合にはくり上がりの回数が1回、奇数ナシの場合にはくり上がりの回数が2回になることがわかりました。

5-2:「筆算の上側6つの数の和」と「下側(答え)3つの数の和」の関係

くり上がりの回数がわかると、答えの各位の和が常に等しくなることの理由がわかります。
なぜなら、「筆算の上側の6つの数の和」と「下側3つの数の和」の差はくり上がりの回数によって定まるからです。
すると、答えの各位の和を和差算によって求めることができます。

偶数ナシの場合：4.29+1.38=5.67（0ナシ）を例に

$$
\begin{array}{rrrr}
&4.&2&9\\
+& 1.&3&8\\
\hline
& 5.&6&7\\
&±0&+1&-10
\end{array}
$$

筆算の下に書いてある ±0、+1、-10 は、「上の2数の和」と下の数の差を表しています。偶数ナシの場合にはくり上がりが1回なので、最終的に「上の6数の和」と「下の3数の和」の差は9になります。
くり上がった10は、上の位の数字としては1でしかないことが理由です。

0ナシの場合には、使える1~9の合計は45なので、あとは和差算が使えます。

下側(答え)の3つの数の和は、(45-9)÷2=18と求められます。

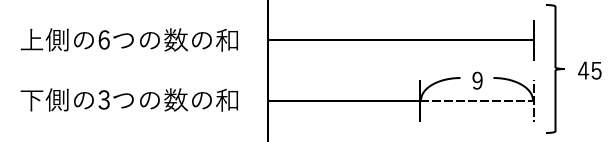
これは0ナシの場合でしたが、2ナシ、4ナシ、6ナシ、8ナシとなった場合には、使える数の合計が2ずつ減っていくので、最後に2で割るために、答えの各位の和は1ずつ減ることがわかります。

奇数ナシの場合：2.58+3.49=6.07（1ナシ）を例に

$$
\begin{array}{rrrr}
&2.&5&8\\
+& 3.&4&9\\
\hline
& 6.&0&7\\
&+1&-9&-10
\end{array}
$$

奇数ナシの場合にはくり上がりが2回なので、最終的に「上の6数の和」と「下の3数の和」の差は18になります。
くり上がりが2回なので、偶数ナシの2倍になっています。

1ナシの場合には、使える数の合計は44なので、あとは和差算が使えます。

下側(答え)の3つの数の和は、(44-18)÷2=13と求められます。

これは1ナシの場合でしたが、3ナシ、5ナシ、7ナシ、9ナシとなった場合には、使える数の合計が2ずつ減っていくので、最後に2で割るために、答えの各位の和は1ずつ減ることがわかります。

6.おわりに

一見なんでもない虫食い算のように見えた問題が、その問題を拡張させて考える中で、いろいろなきまりが見えてくるところが非常に面白い問題だと思いました。
はじめの問題も、その改題として扱った問題も、それぞれで先行実践はあるようです。しかし、それらを合わせた実践や見つけたきまりの理由については、自分の調べられる範囲では見つからなかったので、今回紹介することにしました。

7.参考

田中博史(1995)『算数授業の改革双書 1　追究型算数ドリルのすすめ』明治図書

虫食い算 - Wikipedia

『特設（三桁の足し算から）』

（Webサイトは、全て2022/12/10閲覧）