
折り紙作品「ライオン」について
お久しぶりです。今回は「ライオン」という作品についてです。
はじめに 創作の動機
今回は、面白そうなパーツを見つけたことから創作が始まりました。このようなキッカケの作品はかなり多いです。明確な目的無く紙を触ることから創作に繋がるのですから、普段から紙を触る機会を多く設けたほうが良いな、と改めて実感しました。
展開図

パッと見ではよくある感じの展開図ですが、実は分かりにくい形のズレがあり、その為にミスを誘発するような構造になっています。
創作の過程
頭部の試作

まずは頭部を試作します。いい感じのパーツから顔が作れるだけの範囲が出てくることを確認しました。次は顔を試作します。

前の試作の段階で足りないものはなんだったかといえば、目鼻口です。目はヒダを調整すればどうにかなると考えて、まずは鼻と口を出そうとしました。内部カドが一つ与えられている現状、そこに情報量を加えるのであれば、領域を付加するよりはカドを割った方が効果的でしょう。X(旧Twitter)上では角これなどと言う名前でタグにまとめられている方法ですが、今回はタグを漁っても欲しいものが見当たらなかったので新規に考えることとしました。必要なのは鼻の直角二等辺三角形と、口を作れるだけのスペースです。いくつか試したところ、非常にシンプルな完成形のカド割りに行き着きました。そこまで終わったら目を出していきます。とりあえず鼻筋を半分に折って目にあたる位置に紙を出します。わりとそれっぽくなったので、今度はこれをたてがみと接続します。

非常に良い感じです。次は足を出すことになります。
足を出す
前の写真の段階で、前足の出し方は大体二つに決まっていました。一つは頭部パーツを出せば必然的に出てくる、頭部から真っ直ぐ下に出ている内部カドを使う方法で、もう一つはそのカドと同じ長さの辺カドを使う方法です。内部カドを使うのは早々に辞めました。単純計算で同じ長さのカドを出すために必要な紙の面積は、内部カドを用いた場合だと辺カドを用いる場合の倍、角カドを用いる場合の4倍です。頭部にも多くの面積が取られるのに、そこから距離的にも近い前足にも多くの面積が必要、というのは些か苦しい。

というわけで辺カドを使うことに決めました。
問題はこれからで、上の写真の試作に使われている比率では、後ろ足と尾を折りだすための領域がどう考えても足りません。では領域を付加しよう、となると、今度は試作の端にあたる部分から足が生えてくるようでは胴長なライオンになってしまい格好が悪いです。
この問題を解決するためには、領域を付加しつつも現在手元にある試作の形を変える必要があります。
目をつけたのは、前足から胴体下端までの距離が大変短いことです。元々胴体前縁を前足に利用しようとしていたのですから、前足と胴体の高さがだいたい同じになるのは当然なのですが、完成形を考えるとこれでは都合が悪いです。完成形ではもっと足が長く見えるように胴体を折り込むでしょう。それだったら折り込む幅を事前に想定して、余分な長さになっている領域を足の領域に回せないか、ということを考えました。言葉だけでは非常に分かりづらいので図を提示しましょう。
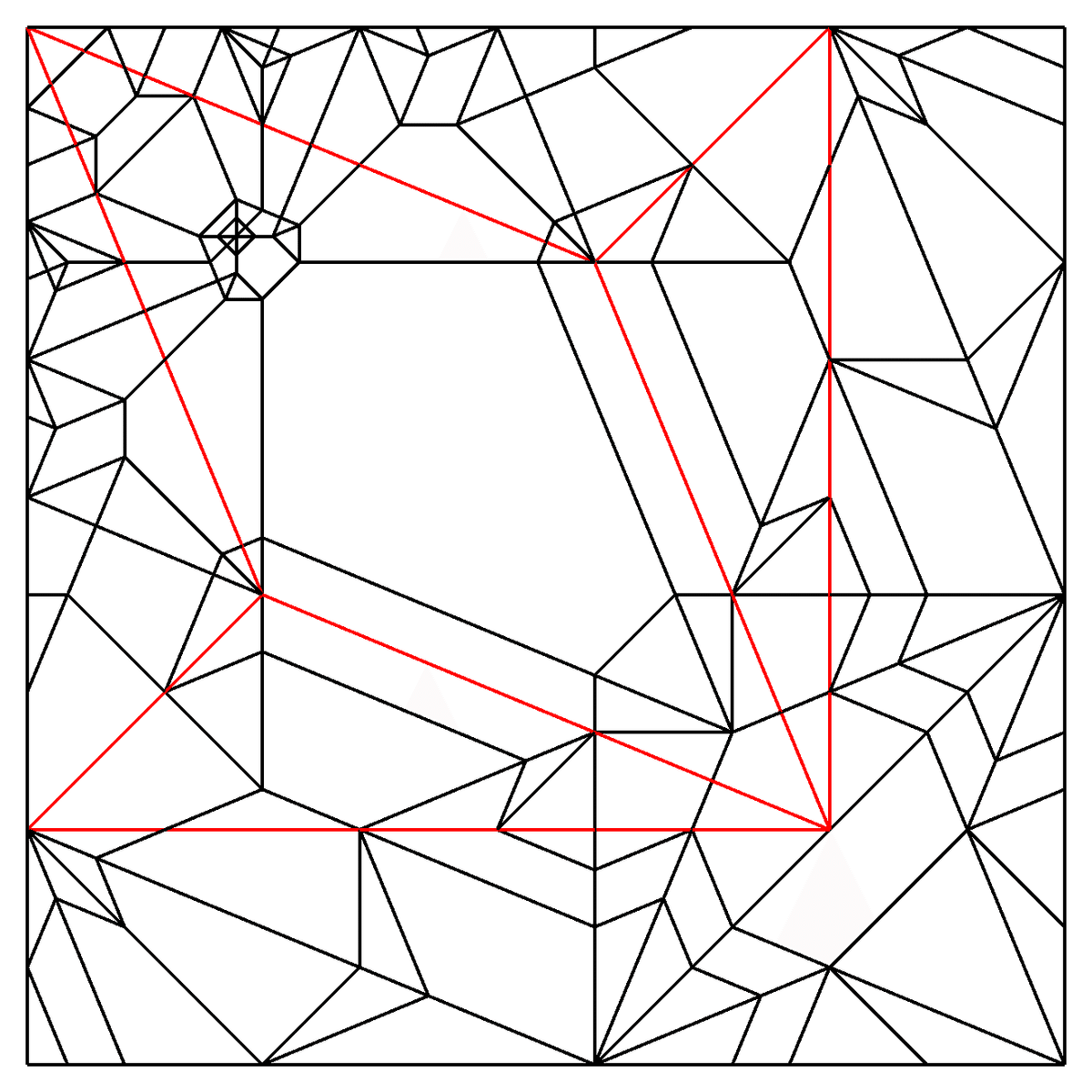
この展開図の黒線は、この記事の冒頭で紹介した完成形の展開図です。そして赤線が試作で用いた魚の基本形の範囲です。尻尾側の角が一つ消えていることに気付くでしょうか?そして、赤線で示した基本形の線の内側と外側に、それよりも短い平行線が一本づつ引かれています。これが先程書いた話です。ちなみに魚の基本形の45度のカド2つが前足になります。
ざっくりと作戦を立てたので、これからは比率を考えることになります。いくつか適当な比率で試作した後、都合の良さそうなものを図に起こし、図から逆算して折りだし比率を出します。


片方は1+2√2、もう片方は3等分です。前に投稿したオヤニラミもそうだったのですが、22.5度にとって都合のよい出方をしたのにも関わらず何故か整数等分になる、ということがしばしばあります。数学的に何らかの必然性があるのでしょうが、僕は文系なのでよく分かりません。
さて、ここまで数枚の試作を作ってきましたが、さっぱり上手くいく気配がありません。どうしようか悩んでいたのですが、上の図を眺めていて気が付いたのは、先程に立てた作戦のための図になっていないということです。

そしてできたのがこの図です。先程の2つの図のうち、1+2√2の図と同じ考え方で、付加領域の接続部と魚の基本形の接続部を重ねました。

試作したところ、足の出方も尻尾の出方もなかなかいい感じなので、このモデルをブラッシュアップするために一回り大きい紙で最終試作をします。
最終試作

さて、これでモデルは完成しました。このタイミングで追加したデザインは、胸部の立体化です。
立体化構造

記事にできてない前作の「カメレオン」で、三角錐を使った立体化の効果の程を実感しました。ジオメトリック・ドームの発明者であるバックミンスター・フラーが授業している映像で、四角形の骨組みよりも三角形の骨組みが強いことを非常に明瞭な形で示した物があります。現実にも橋などによく見られるトラス構造などはこの思想の代表的実例でしょう。なぜこの話を出したかといえば、これは折り紙の立体化を考えるうえで有効であるからです。折り紙作品を立体化する、という課題に対して立ち上がる最大の問題が、剛性をいかにして担保するか、というものです。中が空洞のものは形を保つのが困難です。これに対して様々な対策があります。例えば、作品の中に詰め物をしたり、構造的な対策としては「神谷哲史作品集2」に掲載されている神谷哲史氏の「小鳥」と「セミの幼虫」にて紹介されているものがあります。それらの対策に対してこの三角錐の採用という対策が持つ優位性は、紙の厚みや構造にかかわらず採用しやすいというものがあります。

この写真は前作「カメレオン」の腰部分です。この部分はV字型の段降りを施す事で立体化を実現しています。同様の折り方は随所に見られます。そういった場所の稜線となる筋を強調することで三角形の立体化ができます。
また、三角錐は直方体に比べて押しつぶす力に対して強いという特徴を持ちます。この特性の有利な点として、立体化したあとの加工が容易であるという事があげられます。多少力をかけても潰れず、凹んでも角を引っ張って復元可能である、という状況はガサツな僕にとってはとてもありがたいのです。
完成



今作は、重量感と影の効果を期待してクラフト紙を使いました。それなりに良い効果が出たのではないでしょうか。また、胸部の立体化と顔の作りのために前から見た外見がとても良くなっているのが思わぬ結果でした。これからはこういった効果を意図的に出せれば良いですね。
おわりに
今回は接続の複合や構造の話など、色々と込み入った話が多かったので少しばかり長くなりましたね。分かりづらい場所も多々あったと思われますが、何かしらのの参考になれば幸いです。
