
ジャイアンツの打率はタイガースの打率より本当に高いと言えるのか?
はじめに
10月に入り2024年のプロ野球シーズンが終了しました。今年はジャイアンツが優勝しタイガースの2連覇を阻止しました。
また、打率を見るとわずか5厘差でジャイアンツの方が高いという結果になりました。
ジャイアンツ: .247
タイガース: .242
順位としてはジャイアンツの方が上ですが、打率もジャイアンツの方がタイガースより上と言えるのか気になるところです。😁
そこで今回は、ジャイアンツの打率はタイガースの打率より本当に高いのかを統計的に考えたいと思います。
「打率が本当に高いのか」とは?
「ジャイアンツの打率はタイガースの打率より本当に高いのか」を考えると書きましたが、シーズンの打率はジャイアンツが.247・タイガースが.242なのだから、そりゃジャイアンツの方が高いだろうと思われるかもしれません。
しかし、観測値としての打率だけでは必ずしもそう言い切れるわけではありません。この意味を理解するために「打率が本当に高いのか」とはどういうことなのかを説明します。
真の打率と観測値としての打率
ジャイアンツの打率.247・タイガースの打率.242は実際にバッターがヒットを打った/打たなかったの記録(実際に観測したもの)なので、「観測値としての打率」であると言えます。
そしてもう一つ、2チーム間の打率を比較するには「真の打率」の考慮が必要です。
実際にシーズン打率の記録が出ているのだからそれが真の打率なのではないか?と思われるかもしれませんが、「真の打率 = 観測値としての打率」とは限りません。
「真の打率」と「観測値としての打率」の違いを理解するために、サイコロの例を考えてみましょう。
イカサマなサイロコではない限り、基本的にサイコロの1〜6の目が出る確率はどれも$${\frac{1}{6}}$$です。しかし、実際にサイコロを振ってみると各目の出る割合は必ずしも$${\frac{1}{6}}$$になるとは限りません。
試しに1〜6の目を等確率で出すプログラムを100回実行してみると、各目(数字)が出る割合は以下のようになりました。
$$
\def\arraystretch{1.5}\begin {array} {ll}
\textbf{目(数字)} & \textbf{目が出た割合} \\
\hline
1 & 13\% \\ \hdashline
2 & 23\% \\ \hdashline
3 & 11\% \\ \hdashline
4 & 19\% \\ \hdashline
5 & 12\% \\ \hdashline
6 & 22\% \\ \hdashline
\end {array}
$$
これを見るとどの目も$${\frac{1}{6}}$$(=約17%)の割合で出るとは限らないことが分かります。これは「真の確率は$${\frac{1}{6}}$$だけれども、実際に観測してみるとたまたま11%や23%など真の確率とは離れた数字が出ている」ことを表しています。
観測値として2が23%の割合で出たからと言って、2が出る真の確率が観測値と一致する(23%)とは限らないことが分かります。
打率も同様に考えることができます。
もしかすると真の打率は.300だけれども、実際に観測した打率はたまたま.247や.242だったのかもしれません。真の打率とは、偶然性を排除した真の実力に沿った打率とも言えるでしょう。
打率と正規分布
また、打率の性質に関しても考えてみましょう。
打率とは、1打数でバッターがヒットを打つ/打たないの2つの結果のうち、ヒットを打つ確率のことです。また、1打数でヒットを打つ確率は打数が多くなると正規分布に近似できると言えます。(参考: BellCureve 統計WEB)
一般的な目安として、観測する打数が30を超えると正規分布に近似できます。実際には、ジャイアンツの打数は4752・タイガースの打数は4694であることから十分に大きいため、打率の分布は正規分布に近似できると考えます。(参考: NPB シーズン成績 2024年度 セントラル・リーグ)
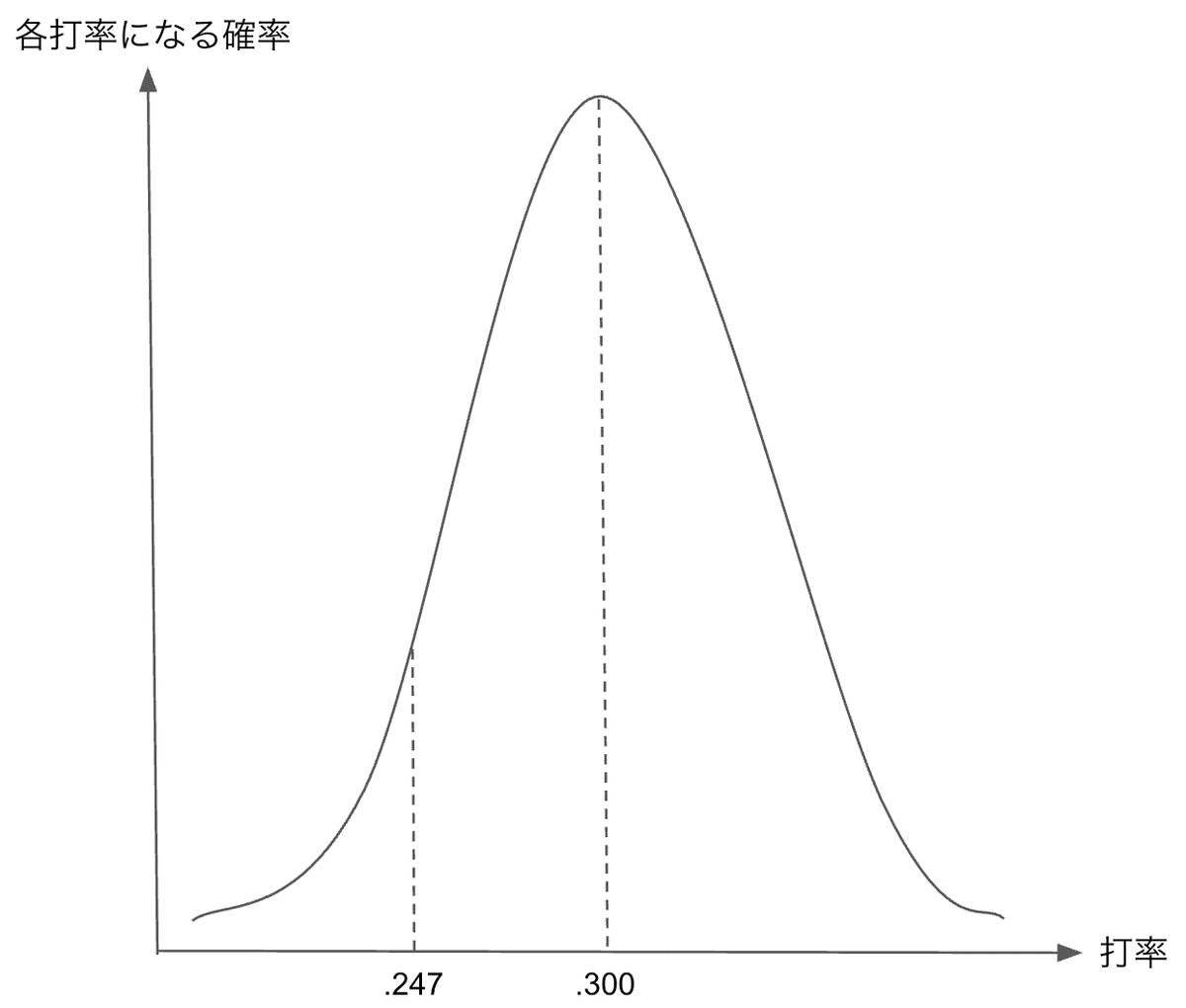
真の打率で比較する
打率が正規分布に近似できることと、真の打率・観測値としての打率を合わせて考えると、打率の大小比較は以下の図のように整理することができます。
緑色のグラフはジャイアンツの打率の分布を、黄色のグラフはタイガースの打率の分布を表しています。
①ジャイアンツの真の打率 > タイガースの真の打率の時

②ジャイアンツの真の打率 = タイガースの真の打率の時

③ジャイアンツの真の打率 < タイガースの真の打率の時

観測値としての打率ベースで考えると「ジャイアンツの打率 > タイガースの打率」であっても、真の打率ベースで考えると「ジャイアンツの打率 <= タイガースの打率」となり得ます。
そこで2チーム間の打率を比較する時は、偶然性のある「観測値としての打率」のみを考えるのではなく、「真の打率」も考えることとします。
以上より、「打率が本当に高いのか」とは「ジャイアンツの真の打率はタイガースの真の打率より本当に高いのか」と言い換えられます。
統計的に確かめてみる
流れ
真の打率で比較すると先述しましたが、実際には真の打率を算出することは困難です。
そこで、いったん「ジャイアンツの真の打率 = タイガースの真の打率」である(先述の②の状態である)と仮定して、観測値としての打率がたまたま差が出たと言えるものなのか、または、たまたま出たものとは言えないくらいの無視できない差である(「ジャイアンツの真の打率 = タイガースの真の打率」という仮定が間違っている)のかを考えていきます。
今回、ジャイアンツの打率はタイガースの打率より本当に高いと言えるのかを考えたいため、「ジャイアンツの真の打率 > タイガースの真の打率」であると言えるか否かの検定を行います。
2チームの観測値としての打率にたまたま差が出たと言える場合は「ジャイアンツの真の打率 = タイガースの真の打率」(先述の②の状態)だろうと考え、たまたま出たとは言えないくらいの差である場合は「ジャイアンツの真の打率 > タイガースの真の打率」(先述の①の状態)だろうと考えます。
検定
使用する用語に関してはBellCurve 統計WEB 23-2.検定で使う用語を参照ください。
いったん仮定すること(帰無仮説)
「ジャイアンツの真の打率 = タイガースの真の打率」
たしかめたいこと(対立仮説)
「ジャイアンツの真の打率 > タイガースの真の打率」
観測値の打率差より偶然な差が出る確率を求めるための数値(検定統計量)
ヒット数・打数・(観測値としての)打率を以下のように表します。データはNPB シーズン成績 2024年度 セントラル・リーグから取得しました。
ジャイアンツ
ヒット数: $${X_1 = 1172}$$
打数: $${n_1 = 4752}$$
打率: $${p_1= \frac{n_1}{X_1} = \frac{1172}{4752} = 0.2466}$$
タイガース
ヒット数: $${X_2 = 1137}$$
打数: $${n_2 = 4694}$$
打率: $${p_2= \frac{n_2}{X_2} = \frac{1137}{4694} = 0.2422}$$
検定統計量($${Z}$$)は以下となります。
$${Z = \frac{p_1 - p_2}{標準偏差} = \frac{p_1 - p_2}{\sqrt{\frac{p_1(1 - p_1)}{n_1} + \frac{p_2(1 - p_2)}{n_2}}} = \frac{0.2466 - 0.2422}{\sqrt{\frac{0.2466(1-0.2466)}{4752} + \frac{0.2422(1 - 0.2422)}{4694}}} = 0.499}$$
帰無仮説を棄却するための基準(有意水準)
今回、「ジャイアンツの真の打率 = タイガースの真の打率」という帰無仮説が間違っていると棄却するための基準(有意水準)を0.05(5%)とします。
観測値の打率差より極端な差が出る確率(P値)
ジャイアンツの真の打率とタイガースの真の打率の分布が正規分布に従う時、この2つ分布の和・差の分布も正規分布に従います。
そのため、この検定統計量$${Z}$$は正規分布に従います。また、$${Z}$$はジャイアンツとタイガースの打率の差(比率に差がないと仮定した2群の差)を標準偏差で割っているため、標準正規分布(平均0・分散1の正規分布)に従います。
そこで、標準正規分布表より$${Z = 0.499}$$の時のP値はおおよそ0.309となります。
帰無仮説の棄却判定
今回、たしかめたいこと(対立仮説)は「ジャイアンツの真の打率 > タイガースの真の打率」なので片側検定(右側検定)を行います。

P値 > 有意水準なので、帰無仮説が間違っているとは言えません。
つまり、「ジャイアンツの真の打率 = タイガースの真の打率」という仮説は間違っているとは言えません。そして、「ジャイアンツの真の打率 > タイガースの真の打率」(対立仮説)が正しいとも言えません。
2チームの打率に差が出たのはたまたま発生したことで、誤差の範囲内であると考えられます。
結論
ジャイアンツもタイガースも同じくらいによく打つ!⚾️
お断り
ジャイアンツとタイガースで、対戦相手のピッチャーが完全に一致しているわけではない点や球場によるヒットの出やすさの考慮は行っていない点など、数字には表れていない差は考慮できていないことから、厳密な検証にはなっておりません。
ぜひ参考程度に見てもらえたらと思います。
この記事が気に入ったらサポートをしてみませんか?
