
Mie散乱(3) - Pythonで書いてみた
5.Pythonのプログラム
5.1 プログラムの流れ

5.2 プログラムのポイント
5.2.1 scipyモジュールを使う
特殊関数である球ベッセル関数$${j_n(z)}$$や球ノイマン関数$${n_n(z)}$$が計算できる関数が収められています。Pythonを使うメリットのひとつです。
scipyをimportして使用します:
$${j_n(z)}$$ ⇒ from scipy.special import spherical_jn
$${n_n(z)}$$ ⇒ from scipy.special import spherical_yn
使用例は、"Python 数値計算ノート − ベッセル関数とノイマン関数"[2],
scipyがインストールされているか確認するためには(jupyter notebookの場合)、
pip list
と入力し、実行(Run)します。モジュールの一覧が表示されると思います。
5.2.2 numpyモジュールを使う
複数の散乱角$${\theta}$$を行列として取り扱い、プログラムを簡単に記述できます。
(1) numpyをimportします:
import numpy as np
(2) 変数thetaを宣言し、散乱角を0°から180°まで、10°ごとに取る:
theta = np.linspace(0,180, 19)
注)thetaは勝手につけた名前で、1行19列の行列になります。
5.2.3 matplotlibモジュールを使う
計算結果が正しいかどうか、グラフにして見るために使います。
importして使う:
import matplotlib.pyplot as plt
使用例は、
ちなみに、今のところ、このサイト[3]は初心者がPythonの使用方法を学習するのに最適だと思っています。
5.2.4 微分を漸化式で計算する
数値的に微分する方法は不安定かもしれないという思いがあり、漸化式を使うようにしました(前掲)。例えば、
$$
\psi_n^{'}(x)=-\frac{n}{x}\psi_n(x)+\psi_{n-1}(x)
$$
数値的に微分する関数はscipyなどにもあるらしいが、試してはいません。
5.2.5 総和を途中で止める基準を決める
$${S_1(\theta)}$$または$${S_2(\theta)}$$では、$${n=1,\cdots,\infty}$$と無限大($${\infty}$$)まで総和を取っています。総和に対して充分な精度が得られ、途中で止めてもよい$${n}$$を$${n_{\mathrm{stop}}}$$とするなら、次式の値に最も近い整数をとるのがよいとされています[4, 5]:
$$
x+x^{1/3}+2
$$
$${x=ka}$$($${k}$$:波数ベクトル、$${a}$$:粒子の半径)
5.2.6 複素数が簡単に使える
numpyモジュールでも、scipyモジュールでも複素数が簡単に使えます。例えば粒子に光の吸収がある場合、屈折率を複素数で定義する必要があります。
5.2.7 複素屈折率の表現に注意する
粒子の複素屈折率$${n_1}$$は、
$$
n_1=n_R-in_I
$$
と、虚数部分の前の記号はマイナスとします。ここで、$${n_R}$$と$${n_I}$$はともに実数。粒子が光を吸収する場合は、$${n_I>0}$$になります[6]。
5.3 自作プログラムの検証結果
5.3.1 検証1
(条件)粒子の直径$${d}$$:600 nm、波長$${\lambda_0}$$:633 nm、溶媒(水)の屈折率$${n_0}$$:1.33、粒子の屈折率$${n_1}$$:1.59-0$${i}$$(吸収なし)
(比較対象)MiePlot [7]
(検証結果)散乱角$${\theta}$$=90°での$${i_1(\theta)}$$と$${i_2(\theta)}$$の値:
自作プログラム:$${i_1(90°)}$$=7.03906873e-01, $${i_2(90°)}$$=8.09189283e-02
MiePlot:$${i_1(90°)}$$=7.03906873e-01, $${i_2(90°)}$$=8.09189283e-02
(評価)一致
5.3.2 検証2
(条件)粒子の直径$${d}$$:100 nm、波長$${\lambda_0}$$:688.8 nm、溶媒(真空)の屈折率$${n_0}$$:1、粒子の屈折率$${n_1}$$:0.09-3.87$${i}$$(吸収あり)
(比較対象)MiePlot [7]、PyMieLab_V1.0 [8]
(検証結果)消光係数$${Q_{\mathrm{ext}}}$$の値:
自作プログラム:0.27618045
MiePlot:0.27618045
PyMieLab_V1.0 :0.27618045
(評価)一致
5.3.3 検証3
(条件)粒子の直径$${d}$$:500 nm、波長$${\lambda_0}$$:633 nm、溶媒(水)の屈折率$${n_0}$$:1.33、粒子の屈折率$${n_1}$$:1.59-0$${i}$$(吸収なし)
(比較対象)MiePlot [7]
(検証結果)散乱強度($${i_1(\theta)}$$, $${i_2(\theta)}$$)の角度依存性:

(評価)一致
5.3.4 検証4
(条件)粒子の直径$${d}$$:20 nm~1 μm、波長$${\lambda_0}$$:633 nm、溶媒(水)の屈折率$${n_0}$$:1.33、粒子の屈折率$${n_1}$$:1.59-0$${i}$$(吸収なし)
(比較対象)MiePlot [7]
(検証結果)散乱強度($${i_1(\theta =90^\circ)}$$, $${i_2(\theta = 90^\circ)}$$)の粒子径依存性:

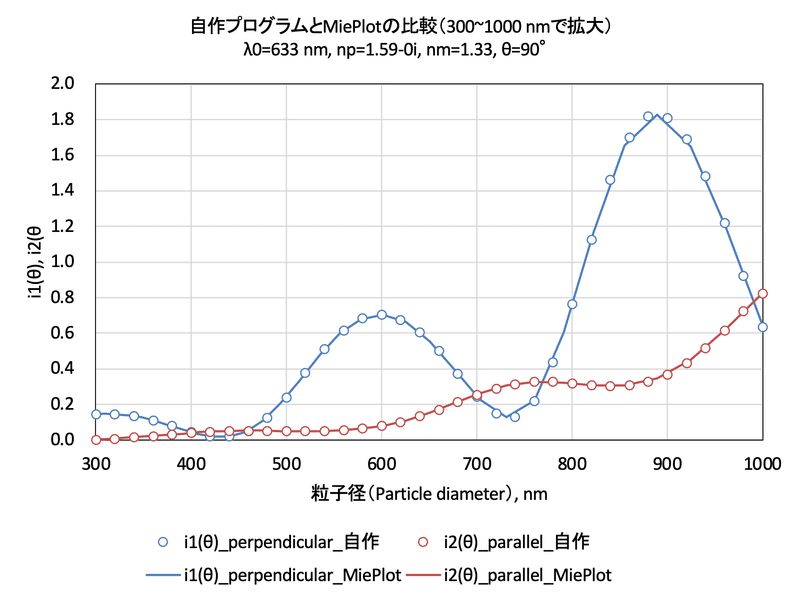
(評価)一致
6.最後に
Pythonを知らないときは、なんでもかんでもExcelで計算していました。しかし、少し高度な計算となると自分の能力ではExcelでは計算できず、その都度あきらめてきました。ひょんなことからPythonを知り、数ヶ月間、ときどき暇を見つけるていどで、曲がりなりにもMie散乱の計算ができるようになりました(ソースコードが稚拙なため、人にはお見せできませんが)。自分が一番驚いています。
文献
[1] ミー散乱(1)
[2] Python 数値計算ノート, ベッセル関数とノイマン関数, https://python.atelierkobato.com/bessel/
[3] note.nkmk.me, Python, https://note.nkmk.me/python/
[4] いえやすの部屋、"ミー散乱 (V) -数値計算プログラム", https://ieyasu03.web.fc2.com/EM/EM_15_Mie_5.html
[5] Craig F. Bohren, Eugene Clothiaux, Donald R. Huffman, "Scattering of Light by Small Particles", Wiley Vch, 2011.
[6] Eugen Hecht, "ヘクト光学I−基礎と幾何光学", 4th Ed., 丸善, 2002.
[7] Philip Laven, MiePlot, http://www.philiplaven.com/mieplot.htm
[8] Dengpan Ma, Paerhatijiang Tuersum, Long Cheng, Yuxia Zheng, Remilai Abulaiti, "PyMieLab_V1.0: A software for calculating the light scattering and absorption of spherical particles", Heliyon, 2022, 8, e11469.
【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。
この記事が気に入ったらサポートをしてみませんか?
