AIを使ったマンデルブロ集合の図形探し

こんにちは、えむしーじじょうのShikiです。

今回はタイトル通りの話とそこで見つけた面白い図形の紹介になります。
知識でしか知らなかったマンデルブロ集合に手を出してみたら、その奥深さにすっかり虜になってしまいました。
様々なことを学ぶきっかけとなったマンデルブロ集合ですが、今回はその中でAIを適用した部分について書きたいと思います。

マンデルブロ集合とは

フラクタルの代表格であるマンデルブロ集合。
名前を知らない人でも下のような図形は見かけたことがあるのではないでしょうか?

この不思議な図形は次の定義によって描くことができます。

次の漸化式

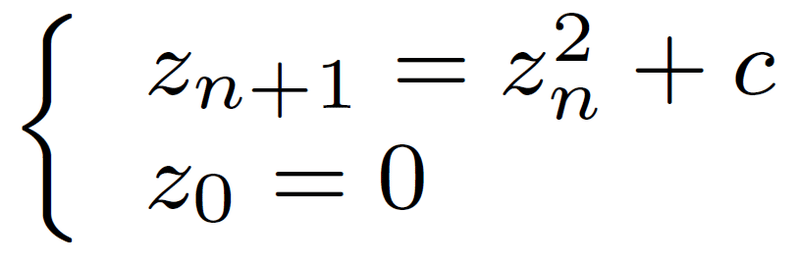
で定義される複素数列 {zn}n∈N∪{0} が n → ∞ の極限で無限大に発散しないという条件を満たす複素数 c 全体が作る集合がマンデルブロ集合である(Wikipedia)

上の画像では横軸が c の実部、縦軸が c の虚部とした場合に、黒がマンデルブロ集合で黄色や紫は発散znが発散する c となっています。黄色や紫の色の違いは発散する速さの違いを表しています。

ある位置を拡大すると

マンデルブロ集合が面白いのはこの図形を拡大していくと、奇妙なフラクタル図形が延々と現れる点にあります。youtubeに投稿されているマンデルブロ集合の拡大動画を1つ紹介します。

何度見ても不思議で面白い。

作って遊んでみる

式が簡単なので自分でも作れそう！と思い、軽い気持ちで手を出してみました。
が、いくつもの落とし穴があり、落ちては這い上がり落ちては這い上がりを繰り返し、ひとまずは形にすることができました。
そうしてできた動画の1つが下です。

1つの動画を作っただけでは飽き足らず、軽い気持ちで手を出してから、この記事を書いている今日までにもう2週間以上経過しているので、しっかり沼にハマっています。

沼にハマった理由の1つは、ずばりバリエーションが無数にあるため。様々な図形が見つかるのは楽しい限りなのですが、(縮小した視点では)世界が広大すぎて探しきれません。

そこで、最近勉強している強化学習を組み合わせて、AIに面白い図形探しを手伝ってもらうことにしました。

AI × マンデルブロ集合

強化学習、つまりはAIにやってもらいたいことは面白い図形探し。とは言っても、面白い図形を定義するのは難しい。そこで、今回は「何かしら模様のある箇所を選んで拡大していく」というミッションを与え、疑似的に様々な図形を探してもらいました。
とは言え、機械学習に関してはひよっこ同然。手動で探した方が早いんじゃないかと突っ込みたくなるくらい一進一退を繰り返した末に、ようやく良い具合にチューニングのできたAIを育てることができました。

その結果の1例が下の動画です

最終的に辿り着いた条件は次のようになります(詳細は省いています)。
AI
Deep Q-Network (教科書にしているこちらから流用)
状態
128×128[pixel] グレースケール
発散速度が速いほど黒、遅いほど白。
行動
下に示す状態の領域から0~24の1箇所を選択

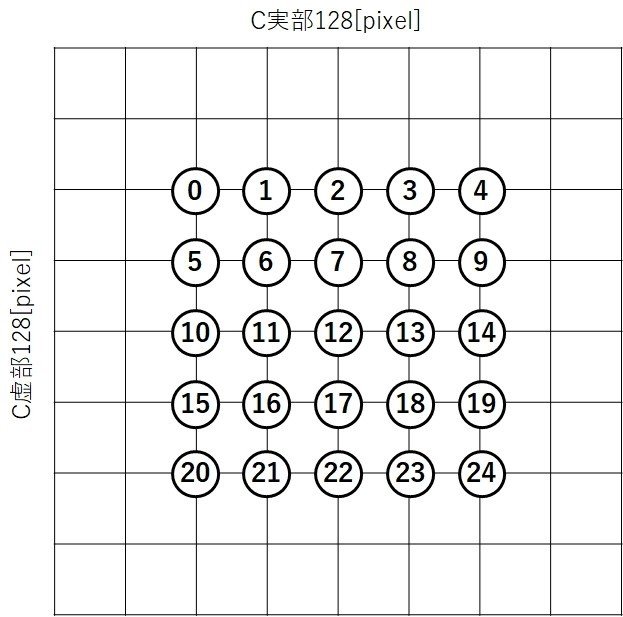
評価(簡略)
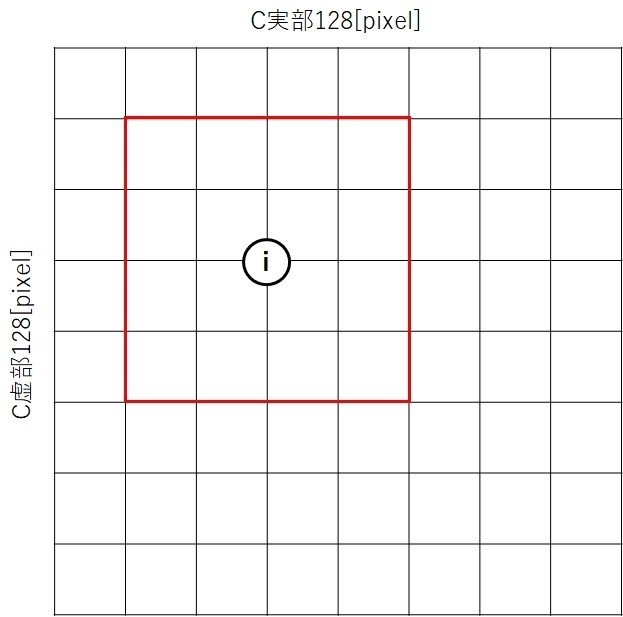
選択したiの4×4ブロック分の領域(赤枠)に対して"選択領域の分散が大きい"且つ"選択領域の大半がマンデルブロ集合で占められていない"場合にプラス、逆の場合にマイナス。
また、プラスの場合はiを中心に2倍に拡大(赤枠領域を全体領域にする)。マイナスの場合は再選択。

1エピソードの終了条件
41回の拡大、または手詰まりで終了。41回で約1e12倍の拡大になります。

奇妙で美麗な図形ギャラリー

最後に、AIが探してくれたマンデルブロ集合の奇妙で美麗な図形達を載せていきます。また、画像と一緒にそれぞれのパラメータも記載いたします。記載のパラメータを入れて計算すれば同じ図形を描画することができます(再現性があるって素晴らしい！)。

パラメータの解説

C(real) = 0.0
中心のCの実部です
C(imag) = 0.0
中心のCの虚部です
r = ±1.0
中心からの図形の縦幅です。アスペクト比が16:9なので横幅はr*16/9になります。
n limit = 500
nの上限です。この場合はz_500で発散しなかったものはマンデルブロ集合とと判定しています。
R = 2.0
z_n+1がRを超えたら発散判定をしています。2を超えた時点で発散することが証明されているそうです。

ギャラリー

C(real) = 0.1120068359375
C(imag) = 0.638021240234375
r = ±0.000322265625
n limit = 1809
R = 2.0

C(real) = -0.746684956561724
C(imag) = -0.148407254991549
r = ±0.000304831581
n limit = 1826
R = 2.0

C(real) = 0.235162322816695
C(imag) = -0.522569730223854
r = ±0.000274348423
n limit = 1857
R = 2.0

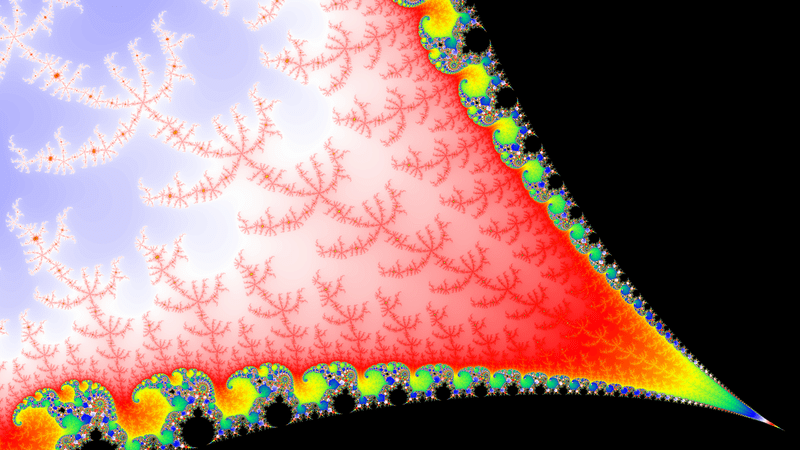
C(real) = 0.431444931030272
C(imag) = -0.210285568237303
r = ±0.00000381469726
n limit = 3680
R = 2.0

C(real) = -0.0123701408058467
C(imag) = -0.654285235802281
r = ±0.00000376335285
n limit = 3688
R = 2.0

C(real) = -0.928145631790161
C(imag) = -0.241136137008666
r = ±0.000000514984131
n limit = 5070
R = 2.0

C(real) = 0.399156056834167
C(imag) = -0.130409942025553
r = ±0.000000338701755
n limit = 5422
R = 2.0

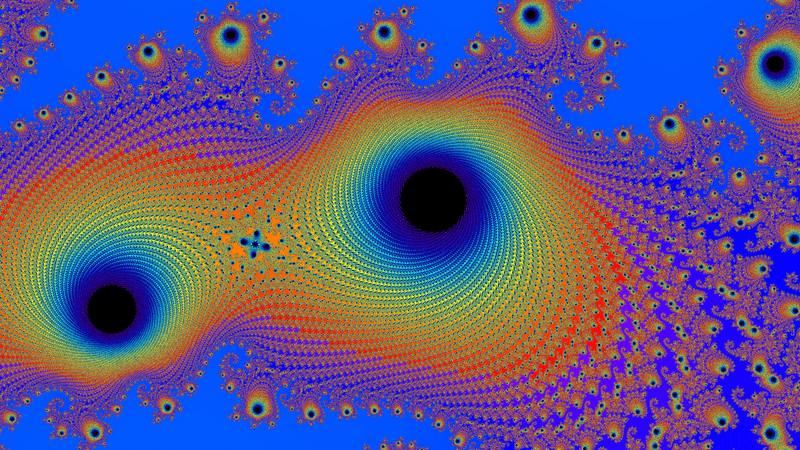
C(real) = 0.22877699136734
C(imag) = -0.520264625549316
r = ±0.0000000596046448
n limit = 7160
R = 2.0

C(real) = 0.373888457566499
C(imag) = -0.596176167950033
r = ±0.0000000074505806
n limit = 9986
R = 2.0

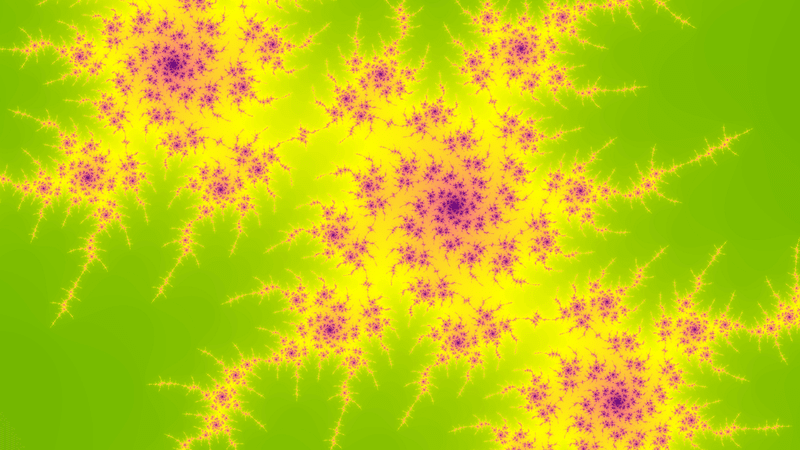
C(real) = -1.35814260283019
C(imag) = -0.0390835766633972
r = ±0.000000000139698386
n limit = 18868
R = 2.0

如何だったでしょうか?
気に入った図形があればうれしい限りです。

AIが探してくれた図形はまだまだたくさんあるので、この記事に付け足すか、新しい記事を投稿するかなど、今後も何かの形で公開したいと思います。

終わり。

参考資料

マンデルブロ集合(Wikipedia)

Pythonで学ぶ強化学習