
電子天秤は何を量っているのか
てん‐びん【天×秤】 の解説
1 支点が中央にあるてこを用いて、物体の質量を分銅と比較測定するはかり。さおの両端に皿をつるすか載せるかし、一端の皿に測る物を、他端の皿に分銅を入れて、さおが水平になったときの分銅の重さで物の重さを知る。上皿天秤・化学天秤など。
参照:デジタル大辞林
初めに
化学合成実験においては様々な必須アイテムが存在しますが、その中でも最も重要といっても過言ではないものは天秤でしょう。反応に使う試薬の定量、容器の重さの確認、収量の計算、分析用試料の調整などなど用途は多岐にわたります。私が学生だった頃、研究室の質を見極めたければ天秤を見ろと言われたものです。天秤の周りにものが散乱していたり天秤自体が汚く校正もまともにされていないような研究室は質が低いということらしいですが、確かに概ね当たっていたような気がします。
そんな天秤ですが、何を量る道具かご存じでしょうか。え?重さを量る道具に決まってるだろ?・・・まぁそうなんですが今回話題にしたいのはより厳密な部分です。すなわち、『電子天秤で量っている重さは「重量」なのか「質量」なのか』というものです。めちゃめちゃどうでもいい?いやいや、冷静に考えてみると意外と奥が深い議題なんですよ。では考えていきましょう。
ちなみに結論から申し上げますと、電子天秤で得られる値は「質量」というのが私の見解です。
質量と重量の違い
そもそも質量と重量ってなにで使い分けるんでしょうか。辞書で調べてみると両者について以下のように記載されています。
しつ‐りょう〔‐リヤウ〕【質量】 の解説
1 物体の慣性の大きさを示す量。または、重力を生じさせる原因となる量。相対性理論によれば、質量はエネルギーの一形態であるとされる。単位はキログラム、その他トン・カラット・匁 (もんめ) など。
2 物の重さ。重量。「このカメラの質量は約1キロだ」
じゅう‐りょう〔ヂユウリヤウ〕【重量】 の解説
1 物の重さ。目方。「規定の重量を超える」「重量をはかる」
2 目方が重いこと。「重量貨物」「重量級」
3 「重さ2」に同じ。
参照:デジタル大辞林
うーん、わからん。質量の説明に重量のことって書いてあるのでなんだか余計に混乱してしまいますね。
ではそもそも「重さ」とは何か調べてみると
おも‐さ【重さ】 の解説
1 重いこと。また、その度合い。「重さを量る」
2 地球上の物体に作用する重力の大きさ。その物体の質量と重力加速度との積に等しい。地球上の場所により重力加速度の値が異なるので、同一物体の重さも異なる。重量。
参照:デジタル大辞林
おぉ、こっちにはきちんと記されています。辞書的には「重さ」=「重量」であり、「重量」=[物体の質量]×[重力加速度]の関係にあるんだということのようです。これはまさしく力学の基礎中の基礎である運動方程式
F=ma
において『F』が重量(重さ)であり『m』が質量、『a』が重力加速度にあたるということですね。もっとかいつまんでいえば「質量」とはある物体に対してかかる力と加速度に影響を及ぼす定数のことであり、「重量」とは重力によってある物体が引き寄せられる時の力の強さのことであるということです。なので、例えば地球上においては極地地域と赤道地域ではかかる重力が違いますから、同じ物体でも重量が変化します。しかし質量は変化しません、一定です。このように重量と質量は似ているようで全く異なる概念なんですね。
天秤で量っているのは?
本稿の目的である電子天秤について考える前に、まず天秤について元代表である上皿天秤を例に考えてみましょう。この道具で得られる情報は質量でしょうか?重量でしょうか?

結論を先に言いますと上皿天秤で得られるのは質量です。なぜならば、上皿天秤はすでに質量が分かっている基準(分銅)と対象となる物体の重さを比較する道具であるからです。極端な例として上皿天秤を火星にもっていくという想定をしましょう。先ほど重量は重力によって変化すると書きました。火星の重力は地球の約1/3ですから、同じ物体でも火星にもっていけば重量が単純に1/3になります。もし上皿天秤が重量を量る道具であるなら、物体と上皿天秤を火星にもっていったときに物体と釣り合う分銅の量は地球の1/3にならなければなりません。しかしそのようなことは起こりません。これは単純に物体だけではなく分銅の重量も1/3になっているためで、上皿天秤にかかる力が両者同じ割合で減少しています。なので物体が同じなら地球上でも火星上でも同じ量の分銅で天秤は釣り合います。
「質量」が判明している分銅という基準を用いて比較しているので、その比率から得られるものも物体の質量になるということです。
ばね秤で量っているのは?
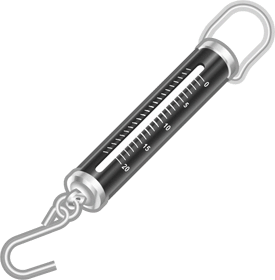
上皿天秤の次にこれまた代表的な重さを量る道具であるばね秤について考えてみましょう。これはいたって単純、量っているのは重量です。ばね秤の原理を大雑把に言えば、ばねに物体を吊り下げた時のばねの伸びを物体の重さに変換するというものです。ばねの伸びがばねに作用する力 (ばね秤の場合は吊り下げた物体の重さ)に比例するという、高校物理の鉄板「フックの法則」を利用しているので、ばね秤は物体の重量を量る道具と言えます。ただ、大体はそうして量った物体の重量を秤についてる質量目盛りを用いて質量に換算していますので、最終的には質量の値は得られますが本質的に得られる量は重量です。
ではそんなばね秤をさっきの上皿天秤と同様火星にもっていったらどうなるでしょうか。答えは明白、本質的に物体の重量をはかるばね秤の場合、測定値は地球上の1/3になってしまいます。また、ばねの伸びは重力だけではなく温度によっても変化してしまうので、mgレベルで重さを量りたい時はそういったファクターを考慮して補正をかける必要があります。
電子天秤で量っているのは?

画像引用:https://ja.wikipedia.org/wiki/%E9%9B%BB%E5%AD%90%E5%A4%A9%E7%A7%A4
さて、いよいよ本題です。上記2例でもお分かりの通り、一口に秤といってもその機構によって量っているのが質量だったり重量だったりします。では電子天秤で量っているのはどちらになるのでしょうか。そのためにはまず電子天秤の機構について調べる必要があります。
電子天秤の機構についてはいろいろな方式があるようですが、分析機器メーカーの一つであるSHIMADZUさんのHPにわかりやすい解説がありました。
SHIMADZUさんによると現在は電磁式とロードセル式がポピュラーなようです。大雑把に言えば電磁式は上皿天秤でいう分銅の代わりに電磁力を用いて物体と釣り合わせ重さを量る、ロードセル式は物体の重さによって変化する電流値を測定して重さを量るという原理のようです。おや?ということは少なくとも現在主流の電子天秤は測定する物体に対してかかっている重力をいろんな方式で検出し、それを重さの値に変換して出力しているということになります。ということは、電子天秤を火星にもっていけば出力される値は地球上の1/3になるということで、これはばね秤と同じです。つまり電子天秤で量っているのは質量ではなく重量であるといえます。こうなってしまうと電子天秤は本質的には「天秤」とは言えないというわけですね。なんだが意外な結果です。
と、いうわけで電子天秤で量っているのは重量・・・となるわけですが実はこの結論は正しくありません(と、私は考えます)。電子天秤についてもっと詳細を調べてみると、やっぱり電子天秤が出力しているのは質量といって良さそうなのです。
どういうことかといいますと、実は多くの電子天秤には校正用分銅が内蔵されていて、それを用いて正しい質量への変換ができるように校正を行うことができるようなのです。SHIMADZUさんのHPに以下のように記載されています。
校正分銅内蔵形の天秤はその内部に校正用の分銅(計量法上は「おもり」)をもっており、それをモーター駆動機構などにより内部で載せ降ろしができるしくみになっています。元々はこの「おもり」そのものには質量の値付けがされているわけではなく、この「おもり」を載せたときの荷重値を、標準となる外部分銅を載せたときの荷重値と比較し、外部分銅の質量のどれだけに相当するかという値を記憶させています。こうすることにより、天びん内部の「おもり」に、標準となる外部分銅の代わりをさせることができ、天びんの感度校正ができる仕組みです。
引用:https://www.an.shimadzu.co.jp/balance/hiroba/qa/qa01.htm#13
確かに地球上の電子天秤をそのまま火星にもっていったら出力される値は1/3になってしまいます。ですが、電子天秤内部の校正用分銅も重量が当然1/3になっているので、それを用いた校正を実行すれば電子天秤は正しい質量を出力することができるようになります。つまり、通常の天秤は物体と基準(分銅)を同時に比較していますが、電子天秤は同時ではなく時間差で比較しているということです。このことを考慮すれば電子天秤では重量ではなく質量を量っているということになります。よかった、これからも堂々と電子「天秤」と呼べそうです。
まとめ
「電子天秤は何を量っているのか」ということについて、調べた情報と私なりの考察をつらつら述べてみました。同時に行っていないだけで実際は電子天秤も通常の天秤と同じように基準 (分銅)と比較して得られる重さの値を出力している、そのため電子天秤で量っているのは質量である。というのが私の見解です。ただ、まぁ私はあくまで電子天秤をただの道具としてしか利用していないしがない化学屋さんですので、専門家の方からしたら何言ってんだこいつと思ってしまうような議論を展開してしまっているかもしれません。その際はご教授いただけますと幸いです。以上、拙文でありますがここまで読んでいただきましてありがとうございました。ね、意外と奥が深かったでしょ?え、そうでもない?あ、そうでしたか、はい。
―本稿執筆者―
十六夜咲夜
この記事が気に入ったらサポートをしてみませんか?
