【算数】市販の解説も間違えた、筑駒の問題!誰が解けたの…?
一般的に中学入試の算数といえば60分前後の時間ですが、筑波大学附属駒場中の入試はなんと40分間しかなく、非常に短いです。当然のように難度も高く、特に注意深く調べなければならない問題が必ずどこかに出題される印象です。誰でも解ける問題を、いかに少ないコストで処理するかが問われているのだと思います。
※国立中なので、いわゆる入試のことは「学力検査」と呼ばれます。
その筑駒ですが、市販の赤い過去問題集において、解説に誤りがあったことを発見しました。最新年度版では改訂されていましたが、元の解説は「答えに影響を与える大きな誤り」でした。つまり、解けたら異能者!ということで紹介です。
【問題】文字が800字並んでいます。
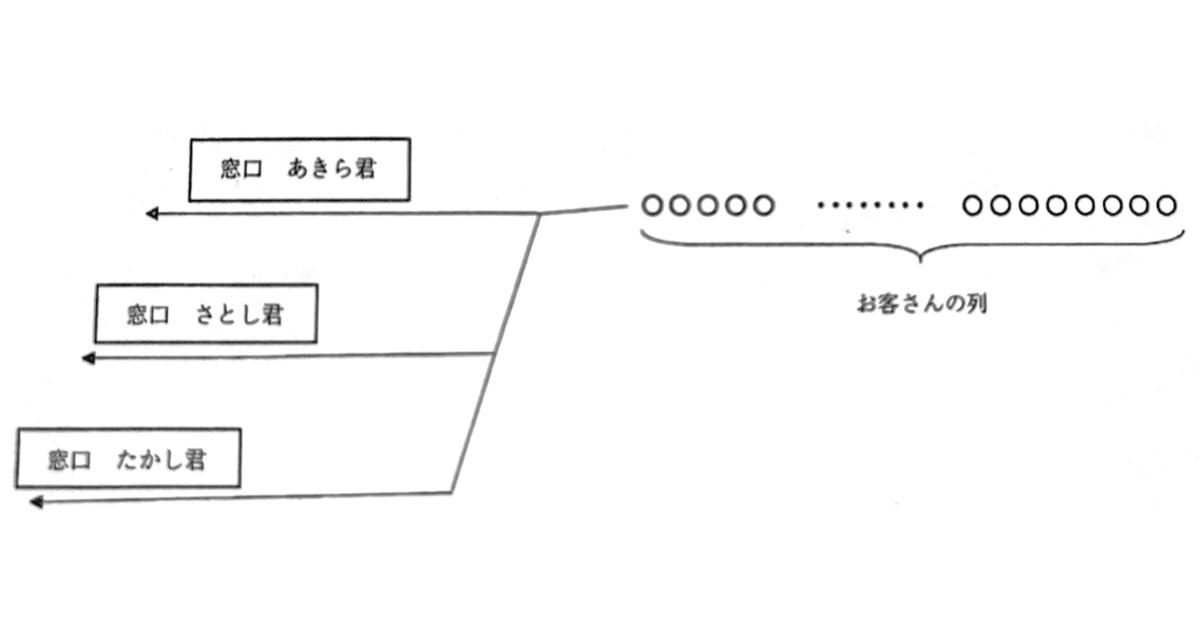
つくこま中学校の文化祭では,開場前に,整理番号1〜545の545人のお客さんが番号の小さい順に一列に並んでいて,次のように3か所の窓口で担当者が受付をします。
受付は以下のように行います。
・あきら君,さとし君,たかし君の3人が,それぞれの窓口で受付を担当します。
・お客さん1人あたりの受付にかかる時間は,あきら君が10秒,さとし君が13秒,たかし君が15秒です。
・お客さんは整理番号の小さい順に,3か所ある窓口のうち,あいているところで受付をします。
・同時に窓口があいたときは、列に近い窓口から受付をします。窓口は,列に近い順に,あきら君の窓口,さとし君の窓口,たかし君の窓口です。
・受付が終わった窓口では,そのとき列の先頭にいるお客さんの受付がすぐに始まります。お客さんが列から窓口へ移動する時間は考えません。
・1か所の窓口に,同時に2人以上のお客さんが行くことはありません。
文化祭の開場と同時に,整理番号1のお客さんがあきら君の窓口に,整理番号2のお客さんがさとし君の窓口に,整理番号3のお客さんがたかし君の窓口に行くとして,次の問いに答えなさい。
(1) あきら君が受付をする,ちょうど30人目のお客さんの整理番号を答えなさい。
(2) (ア) 整理番号165のお客さんの受付が終わるのは,文化祭の開場から何秒後ですか。 (イ) 整理番号165のお客さんの受付をするのは,あきら君,さとし君,たかし君の3人のうち誰ですか。
開場からしばらくして,窓口のあきら君,さとし君,たかし君のうち1人が,あるお客さんの受付を終えると同時に,ゆたか君と交代しました。ゆたか君がお客さん1人あたりの受付にかかる時間は8秒です。この結果,文化祭の開場からちょうど2022秒後に,整理番号545のお客さんの受付が終わりました。
(3) ゆたか君は、文化祭の開場から何秒後に,あきら君,さとし君,たかし君のうち誰と交代しましたか。
本番ならトータル10分程度で処理したい問題です。(3)のみ解説します。
【解説‐偽‐】a fake Solution
最後の545番の人が終わる付近の様子を考える。
・あきら…2022秒÷10秒/人=202人あまり2秒
・さとし…2022秒÷13秒/人=155人あまり7秒
・たかし…2022秒÷15秒/人=134人あまり12秒
ゆたか君と交代せずに受付した場合、3人とも2022秒ちょうどで終えられないので、545番の人を担当するのは、誰かと交代した後のゆたか君と決まる。もしあきら君やさとし君と交代して最後の8秒で545番の人を受付することを考えると、その前にたかし君の窓口が12秒間あいているはずなので、そちらに行っていなければおかしい。よって、交代したのはたかし君と決まる。
時間を求めるためにつるかめ算をする。545−(202+155)=188人を2人で受付するので、(2022−8×188)÷(15−8)=74人…たかし君が受付する人数。15秒×74人=1110秒後にたかし君と交代。
【解説‐真‐】The TRUE Solution
(上の解説と同じ)
・あきら…2022秒÷10秒/人=202人あまり2秒
・さとし…2022秒÷13秒/人=155人あまり7秒
・たかし…2022秒÷15秒/人=134人あまり12秒
よって、545番の人を担当するのはゆたか君しかいない。3人それぞれと交代した場合について調べる。
あきら君と交代…545番を受付する直前にたかし君の窓口には544番の人が入っているはず。よって、545−(155+134+1)=255人をあきら&ゆたかで受付。(2022-8×255)÷(10-8) →引き算できない。不適。
さとし君と交代…545番を受付する直前にたかし君の窓口には544番の人が入っているはず。よって、545−(202+134+1)=208人をさとし&ゆたかで受付。(2022-8×208)÷(13-8) →割り切れない。不適。
たかし君と交代…545−(202+155)=188人を2人で受付するので、(2022−8×188)÷(15−8)=74人…たかし君が受付する人数。15秒×74人=1110秒後にたかし君と交代。
【解説の解説】What's wrong?
一体何が違うのか??ズバリ、2段落目「たかし君に決まる」が違います。というのも、問題には「2022秒後に545番の人の受付が終わった」と書かれているのに、解説では「2022秒後に545人全員の受付が終わった」という前提で解いています。…ほら、間違っていないように見えますね?
ここでの整理番号とは「受付を開始する順番」であって「受付が終わる順番」はバラバラであるはずです。たまたま速い窓口なら、後から受付開始した人が先に入場できるかも知れません。よって「2022秒後に整理番号が最後の人の受付が終了し、その数秒後に一つ前の人が終了する」場合の検証をしていなかったことが誤りです。

ただ、それでも答えは合っていますね。検証を省いたくらいは良いのでは?という気もしますが、違います。2022年度の問題だったからたまたま合っていたに過ぎません。もしこれが「2024秒後」に545番の受付終了という問題だったら…
・あきら…2024秒÷10秒/人=202人あまり4秒
・さとし…2024秒÷13秒/人=155人あまり9秒
・たかし…2024秒÷15秒/人=134人あまり14秒
→元の解法を採用すると、誰と交代しても矛盾が起こって答えが出ないことになりますが、後者の解法なら、さとし君と936秒後に交代することで成立します。つまり、元の解法は「間違っていたがうっかり当たっていた」だけなのです。
【問題に問題】TRULY TRUE?
出版物の良し悪しということより、この問題そのものに疑念が残ります。
「筑駒の作問者は、正しい解法を想定していなかったのではないか?」です。
理由は2つ。まず問題として不自然です。ここまで長い説明を書いて一見「丁寧に作業できるかを見る問題」なのに、落とし穴を用意することが不自然。また、並んでいる人は600人とかでもいいのに、わざわざ「全部で545人」と書いてあるため、勘違いされやすい問題となっている。
次に、試験として不自然。「学力検査」の目的とは、文字通り学力を検査し、より能力の高い生徒を獲得するという篩い分けのはずです。ところが正しく考えてより多くの時間を割かなければならなかった優秀な人が、誤りに気づかず楽をした大多数の人と同じ結果となるこの問題においては、そのフィルターは機能しません。むしろ正しく見抜いたせいで、途中で答案を消したり、別の問題に残り1分を使わざるを得なかった受験生もいるかも知れません。
もちろん本番が全てなので「そういう入試だった」以外の結論はありません。あるいは、解答用紙の計算欄も見ているのかも知れません(採点基準は不明です)。だとしたら試験の目的に適う、素晴らしい良問です。
自分が受験生だったらザワザワしますが、総じて面白い問題です。ご参考まで。
2023年12月23日
おいしいコーヒーが飲めると集中力も想像力も高まります。 よろしければコーヒーサポートをお願いいたします😌☕
