2021年関東１都６県の公立高校入試（数学）を全てやっつけた奮闘記

２月の訪れは恐怖である。

毎年、公立高校入試の解説をねちねちと書いたのが功を奏したのか、グーグルで『公立高校入試　解説』とか『高校入試　解説』で検索すると、ありがたいことに私のページが最初にでてくる。受験期の２月は閲覧数が伸び、ありがたきことに注目されるが胃が痛い。

わかんない問題が出てきたらどうしよう。

高校受験の数学の経験値はそこそこあるものの、運良く閃いてクリティカルヒットをかませる保証なんてどこにも無い。なるべく早めに帰り、当日～翌日の朝までに仕上げるつもりだったのでタイムリミットも厳しく、なにより閲覧数に比例してプレッシャーがヤバイ。

どんな問題がでてくるかと期待３割、不安７割で、いつも精神が不安定な時期である。そのうえ、１月下旬の渋谷幕張あたりから中学受験の解説も書き続けていたので相当体力が減っている。こんな調子で連戦に持ち堪えられるのか…。

以下、気になった問題をピックアップし、解説を織り交ぜながら裏話やちょっとした講評などを記していく。（％は正答率です）

１戦目；神奈川（２月15日）

解説ページはこちら➡2021年度神奈川【数学】解説

今年は千葉前期がないため、神奈川が初戦となる。神奈川といえば難易度の乱高下が激しく、過去問では出題者の個人的趣味??のような問題を見かけたこともあり、油断ができない。どうせ３（ア）で変なのを出してくるので、２までは快速でいきたい。

大問２（カ）46.8％

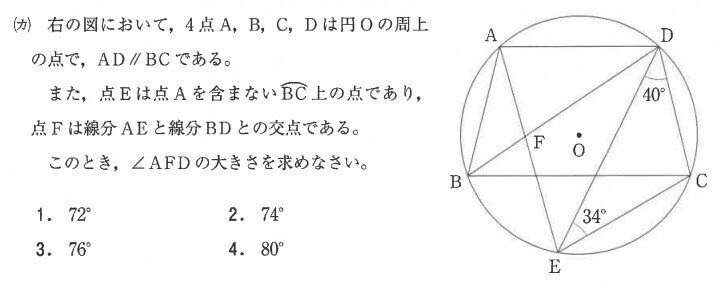
手が止まる。

円に囲まれた角度の問題は小問集合でよく出てくる。たいていは一瞥しただけで解法がシュッと見えるものが多いが見えない。ヤバイ:(；ﾞﾟ'ωﾟ'):

それでも角度なので、わかるところからしらみつぶしていけばいずれたどり着く。とりあえず円周角と平行線を使ってみよ。

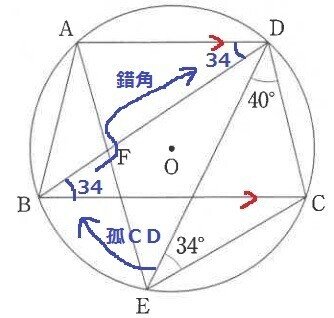
ここから補助線だろうけど、解説ブロガーの意地もあり、うまい芸当はないものか考えてみた。いきなり∠ＡＦＤに飛びつくのではなく、外角定理で分解して∠ＡＦＤ＝∠ＢＡＦ＋∠ＡＢＦとし、円周角で∠ＢＡＦを∠ＢＤＥに移したとして図形をジーと見ていると、

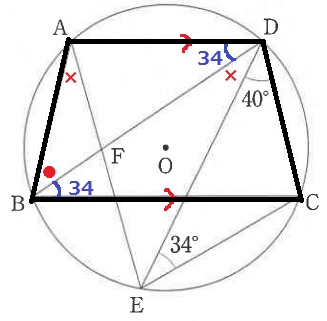
内接四角形ＡＢＣＤが主張してきた。

対角の和が180度だから、
●＋34＋34＋×＋40＝180
●＋×＝72°→∠ＡＦＤ＝72°

補助線を描かなかったけど、思いつきにくい解法だと思う。正答率はあまり良くはなさそう。とにかく時間が厳しいので、少しトライして無理そうであれば飛ばしてしまうのが無難である。

大問３（ア）ⅱ7.8％

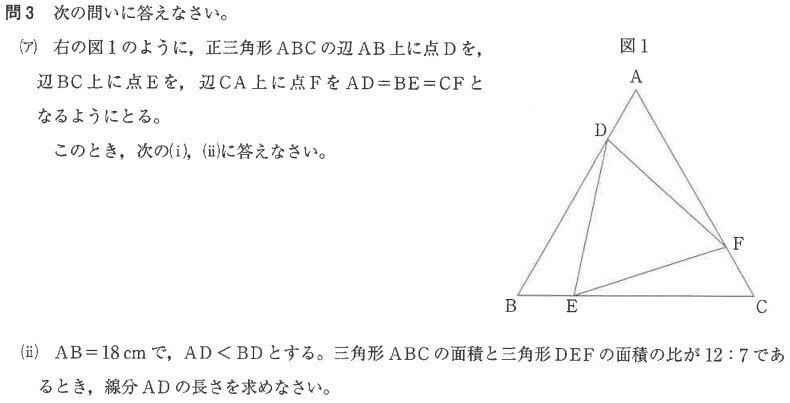
前問で△ＡＤＦと△ＣＦＥの合同は証明済み。全体の雰囲気からも120度回転させると元の図形とピッタリ重なる（回転対称）と察しがつく。

△ＤＥＦを⑦とおくと、周りの三角形は（⑫－⑦）÷３＝〇５/３
分数が邪魔くさいのでこれを払ってみた。

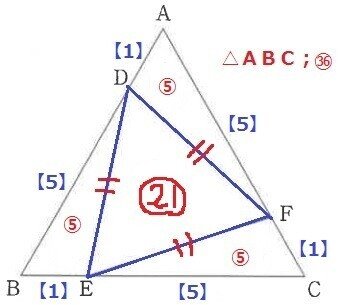
△ＡＢＣが㊱で平方数。ロクロク36。正三角形ＡＢＣの１辺を【６】としてＡＤ＝【１】ＤＢ＝【５】とすると、周りの３つの三角形の面積は【１】×【５】＝⑤。ＡＤの長さは18×１/６＝３ｃｍ

運の良さもあって所要時間１分ちょい。

今年は呆気ないなと思ったが、本問で悲鳴を上げた人は多いらしい。フォロワーさんによると、どうやら垂線を引いて三平方を使う手があるんだとか。解説動画でそのようなことをやっている人を見たら、式がめっちゃ長い！数字の出所を探すのが大変で読解に苦労した。よく計算ミスしないな。

私は中学受験の算数でこの形を見たので、むしろ三平方が頭のなかになかった。問題文から面積比が与えられたので、素直に比で終息を図るのが良いんじゃないかな？もっとも、隣辺比の値を和積の方程式で立てるのは、やや特殊形である。

大問３（イ）32.9％

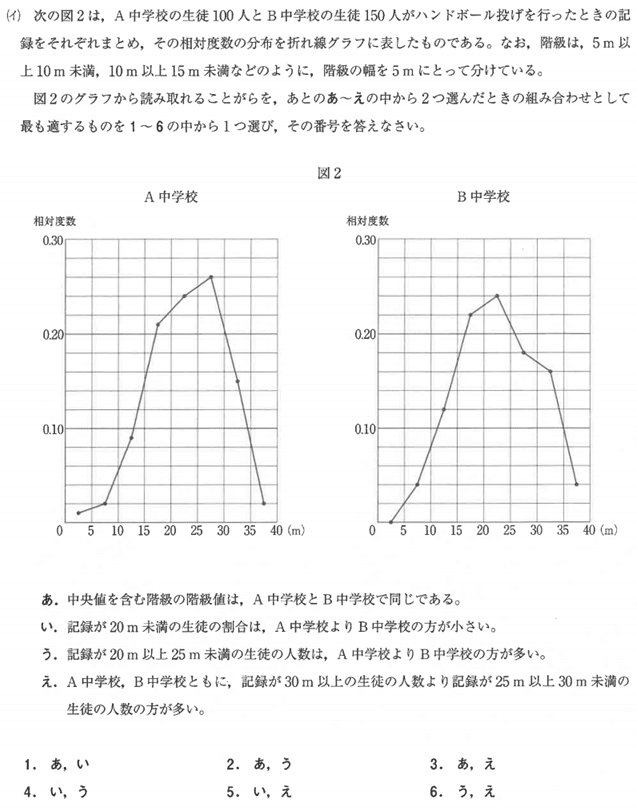
ハナクソ問題である。

相対度数を折れ線で示したことに新規性を見出したいのだろうが、折れ線というのは基本的に推移の表示に使うのであって、度数分布表のグラフは普通、ヒストグラムを用いる。

選択肢も始めから終わりまで小数の計算ばかり強いられて精神的に苦痛。１個くらい『い：Ａ中学校の最頻値は22.5です→×』があって良かった。

どこかの県でも資料問題でやけに数の多い値をいちいち足して個数で割って平均を出させたあと、違う角度から再度平均を出させる無価値の二度手間があったが、それを思い出してさらにイライラが(*'ω'*)ｗ
ちなみに、正答は【２】である。

大問６（ウ）3.4％

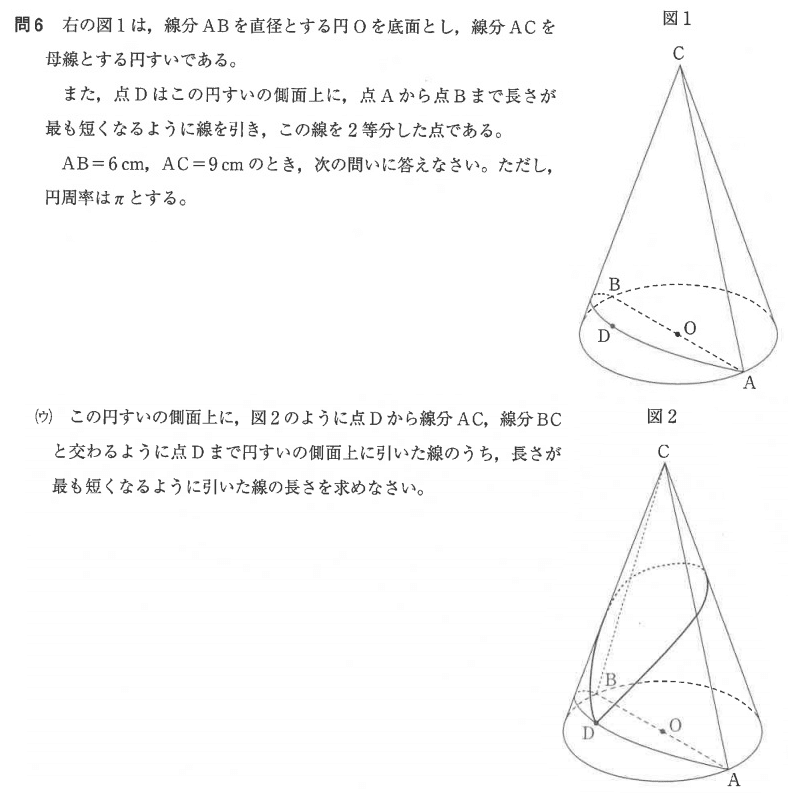
ラストの問題。

前問の（ア）円錐の体積、（イ）円錐の表面積を求めさせ、展開の乏しさにやつれたが、（ウ）はなかなか興味深かった。

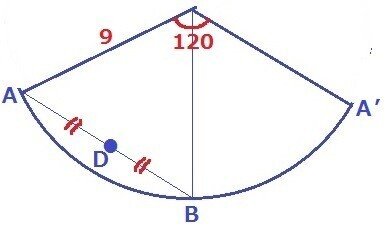
最短距離なので展開図を作成する。側面の扇形は360×半径/母線で120°。だいたいこの手の問題はあとで三平方が使えるように有名角が登場する。問題は２本目の最短距離をどう記述するか。

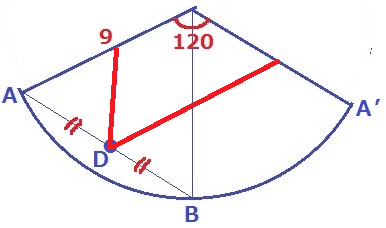
強引に描くとこんな感じに折れ曲がってしまい、すごく出しにくい。でも、ジーと見つめていたら、Ｄのあたりが光線の入射角と反射角に見えてきた。そうだ、鏡の世界を作ろう。