
pythonで日本の食料自給率を時系列分析してみた
Ⅰ.はじめに
現在、Aidemyにてpythonを利用したデータ分析コースを受講しています。
今回、コースの総仕上げとして、実際に自分で考えてデータ分析をしてみようということで、データ分析の目的の設定~実際に分析をしてみて、結果・精度がどうなったのかまでを紹介したいと思います。
内容は、タイトルにもある通り、日本の食料自給率についての予測です。
このような内容にした理由としては、もともと環境問題に興味があり、データ分析を利用して、それらの問題解決に貢献できないかと思ったのがきっかけでした。
はじめは「フードロスの発生量の予測」を行いたかったのですが、色々と調べてみた結果、データ数が少なく断面する形となりました。そのため、方向性を変えて、昔から記録が残っている、日本の食料自給率にフォーカスを当てることにしました。
食料自給率について
まず日本の食料自給率について説明します。
食料自給率とは、「国の食料供給に対する国内生産の割合を示す指標」です。つまり、私たちの国で食べられている食料の中で、どの程度国産が含まれているかを可視化したものということになります。
この食料自給率ですが、日本では2種類の指標が使われています。それが食料自給率を熱量で換算する「カロリーベース」と金額で換算する「生産額ベース」です。
これらは簡単に言うと、
カロリーベースは、国民ひとりあたりの1日の接種カロリーの中で国産が占める割合を表したもの。
生産額ベースは、国民に供給される食料の生産額の中で国内生産された額が占める割合を表したもの。
ということになります。
この2種類のうち、カロリーベースの方が数値が低くく、聞きなじみがあるため、こちらを採用し分析を行っていきたいと思います。
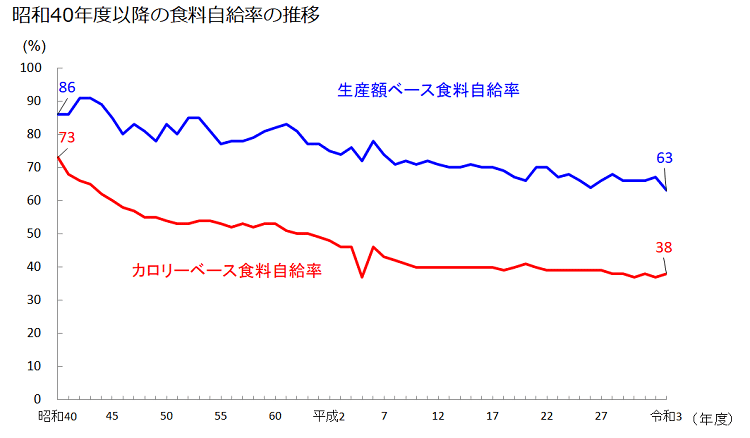
また、日本は2030年度までにカロリーベースでの食料自給率を「45%」まで上昇させることを目標としているため、今回は今までの食料自給率の推移から現時点でこの目標が達成可能なのかについて予測していきたいと思います。
実行環境
google colaboratory
Ⅱ.データ分析の流れについて
実際にデータ分析を行うに当たって以下のような流れで分析を行っていきたいと思います。
目的の設定
データ取得
データの前処理
学習モデルの構築・学習
データ分析
解釈・評価
1.目的の設定
まずはじめにデータ分析を行う目的決めから入ります。
ここを曖昧にしてしまうと、「どのようなデータを収集すればいいのか」や「どのような分析手法が適切か」などデータ分析の方向性がブレてしまうことに繋がります。
今回の場合は、日本の食料自給率の推移から、「2030年度のカロリーベースでの食料自給率45%」は達成可能かどうかについて機械学習を利用して予測したいと思います。
2.データ取得
目的を決めたら、次にその目的達成に必要なデータを取得していきます。
基本的には、インターネットなどから必要なデータのデータセットを取得して、それを利用していきます。
データセットは主に以下のサイトから取得できます。
AINOW
Lionbridge AI
Kaggle dataset
ただ、今回は"e-Stat"から農林水産省が公開している食料需給表をデータとして取得しました。
使用するライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import itertools
import datetime
from statsmodels.tsa.arima_model import ARIMA取得したデータの読み込み
#データの読み込み
file_food = pd.read_csv("/content/食料自給率.csv",encoding="shift-jis",header=11,index_col="自給率") 
こんな感じの1960年度~2020年度のデータを取得できました。
このデータを利用してデータ分析を行っていきます。
3.データの前処理
先ほど取得したデータで分析を行っていくのですが、今のままでは余計な情報が多いので、まずデータの前処理をして学習に必要なデータのみ抽出していきます。
#カロリーベースの食料自給率のみ抽出
file_food = file_food.loc["供給熱量ベースの総合食料自給率"]
print(file_food)
print(type(file_food))
出力結果
1960年度【%】 79
1961年度【%】 78
1962年度【%】 76
1963年度【%】 72
1964年度【%】 72
..
2016年度【%】 38
2017年度【%】 38
2018年度【%】 37
2019年度【%】 38
2020年度【%】 37
Name: 供給熱量ベースの総合食料自給率, Length: 61, dtype: object
<class 'pandas.core.series.Series'> 抽出した結果、Series型として出力されたので、データフレーム型に変換します。
また、今のままではindexが文字列として認識され、この後の時系列分析に支障が出るため、indexを日付に変換します(今回、年間データを使用しているため本来、月以降の日付はないが、分析をスムーズに行うため各日付データは月初めとして設定する)。
#Seriesとして渡されるので 、データフレームに変換
file_food =pd.DataFrame(file_food)
#日付を月初め ("YS")に設定して、インデックスの作成
file_food.index = pd.date_range("1960","2020",freq="YS")
#カラムの作成
file_food.columns = ["食料自給率(cal)"]
#データフレームの数値はstr型になっているのでint型へ変換
file_food = file_food.astype(int)
print(file_food)
出力結果
食料自給率(cal)
1960-01-01 79
1961-01-01 78
1962-01-01 76
1963-01-01 72
1964-01-01 72
... ...
2016-01-01 38
2017-01-01 38
2018-01-01 37
2019-01-01 38
2020-01-01 37
[61 rows x 1 columns]
<class 'pandas.core.frame.DataFrame'> これでデータの体裁は整いました。
ただ、このままではデータの傾向などが掴めないので、次はデータの可視化をしていきます。
3.1データの可視化
まずは今回使用するデータに欠損がないかを確認します。
#欠損値の確認
print(file_food.isnull().sum())
出力結果
食料自給率(cal) 0
dtype: int64 "0"なので欠損はなく、すべての年度にデータが存在することが確認できました。
次にデータの可視化をしていきます。
#データの可視化
plt.plot(file_food)
plt.title("Food self-sufficiency rate(cal)")
plt.xlabel("year")
plt.ylabel("Food self-sufficiency rate(cal)")
plt.show()
上記のような折れ線グラフが描けました。
この結果を見ると、2020年に近づくにつれ、徐々に食料自給率が低下していっているのがわかります。これは日本人の食生活が米中心から欧米風に変化し、小麦や肉を多く摂るようになっていったことが要因であると考えられます。
また、グラフを見ると1990年と2000年の間で数値が急低下している部分も見受けられます。
#データの可視化 (1990-2000)
plt.plot(file_food)
plt.title("Food self-sufficiency rate(cal)")
plt.xlabel("year")
plt.ylabel("Food self-sufficiency rate(cal)")
plt.xlim("1990","2000")
plt.show()
可視化してみると1993年に急低下していました。
調べてみると、この年は記録的な冷夏による米不足(1993年米騒動)が原因で、翌年には気温も通常に戻ったことにより、食料自給率の低下は一時的なもののようです。
3.2時系列分析について
可視化した結果、今回使用するデータは数値が徐々に低下する傾向がみられました。
次にこのデータをモデルに学習させ、予測を行っていくのですが、その前に時系列分析とは何かについて確認していきます。
時系列分析とは、
時間の経過順に並んだデータをもとに、変動要因を、長期的な傾向、周期的な変動、不規則な変動などの要素に、統計的な手法を用いて分解し、将来の値を予測するもの。
という分析です。つまり、時系列に並んだ1つのデータを長期的な傾向(トレンド)、周期的な変動(季節変動)、不規則な変動(残渣)に分解したうえで、それらのデータを統計的な手法を用いて将来を予測するという分析になります。
試しに今回使用するデータを処理前のデータ(原系列)、トレンド、季節変動、残渣に分けてみます。
#季節調整を行い原系列をトレンド 、季節変動、残差に分けて出力
sm.tsa.seasonal_decompose(file_food).plot()
plt.show()
4種類に分解してみた結果、トレンドは”負のトレンド”、季節変動はないことがわかりました。恐らく、使用しているデータが年間データであることが要因だと思います。
次に、時系列データに特有な統計量である「自己共分散」とりわけ「自己相関係数」について見ていきます。
自己共分散とは、同じ時系列データでの別々の時点同士での共分散で、これを様々な値間で比べられるようにしたものを「自己相関係数」と言います。
簡単にいうと自己相関係数とは今のデータx年が過去のデータy年と比べてどれだけ似ているか(影響を受けているか)を数値で表した値となります。
では、実際に自己相関を可視化してみます。
#自己相関関数の出力
sm.tsa.stattools.acf(file_food,nlags=60)
出力結果
array([ 1. , 0.92124509, 0.85573588, 0.78803134, 0.7308911 ,
0.66767484, 0.59794231, 0.54030801, 0.48481526, 0.43227685,
0.38908752, 0.34755366, 0.31553623, 0.28667833, 0.26072894,
0.23153635, 0.20902738, 0.18862211, 0.16420666, 0.13464952,
0.10412021, 0.07107683, 0.04135235, 0.00636464, -0.0282585 ,
-0.06781816, -0.10935998, -0.1403674 , -0.18813067, -0.21788504,
-0.24905979, -0.27942176, -0.29978122, -0.31908484, -0.30657407,
-0.32579403, -0.33245955, -0.33580617, -0.33786189, -0.3344492 ,
-0.33282146, -0.33062398, -0.32664153, -0.32253757, -0.32167681,
-0.3211806 , -0.31902096, -0.31200052, -0.30987873, -0.30884266,
-0.30343185, -0.29198289, -0.27781466, -0.25950678, -0.23965698,
-0.21769552, -0.18851058, -0.15706257, -0.12597913, -0.08528761,
-0.04519573])
#グラフ化
sm.graphics.tsa.plot_acf(file_food,lags=60)
plt.show()
実際に可視化してみました。
この結果、トレンド通り、最初は正の相関がありましたが、徐々に負の相関に変化していき、最後は相関がほぼなくなっていっていることがわかります。
また、時系列データには自己相関係数とは別にもう1つ重要な統計量があります。
それが「偏自己相関係数」です。
自己相関係数は、過去とのデータの相関を求める値でしたが、この場合、例えば7日間の時系列データのうち、2日目と3日目に相関があった場合、それ以降の3日目と4日目、4日目と5日目・・・など、他の日付間にも相関がみられる可能性があります。
このような影響を考慮して相関係数を求めたものが偏自己相関係数になります。
偏自己相関係数も実際に可視化してみます。
#偏自己相関関数の出力
sm.tsa.stattools.pacf(file_food,nags=29)
出力結果
array([ 1. , 0.93659917, 0.06129456, -0.05293848, 0.04099116,
-0.08127605, -0.12157523, 0.04978014, -0.0185906 , -0.03304948,
0.06689953, -0.01622064, 0.03727113, 0.02877866, -0.01131621,
-0.07053338, 0.04003616, -0.00730942, -0.08212883, -0.08270968,
-0.06141366, -0.1041952 , -0.01099131, -0.10208021, -0.09248894,
-0.13968735, -0.16901844, 0.01311052, -0.38430632, 0.04875405])
#グラフ化
sm.graphics.tsa.plot_pacf(file_food,lags=29)
plt.show()
可視化の結果、一定の周期は見られず、季節変動性がないことが確認できました。
3.3これまでのまとめ
データの前処理では、以下の事を行いました。
・欠損値の確認
・データの可視化
・トレンド、季節変動・残渣の分解
・自己相関・偏自己相関の確認
以上のことから、今回使用するデータには負のトレンドがありますが、年間データのため、季節変動がなく、一定の周期は見られないことがわかりました。
これらを踏まえて、モデルの構築を行っていきます。
4.学習モデルの構築・学習
4.1学習モデルについて
まずは学習させるモデルについてです。
時系列分析におけるモデルは複数種類あります。
①AR(自己回帰)モデル
⇒現在の値は過去の値のみに影響を受けると考えるモデル
ex.今日の売り上げを昨日の売り上げから予測する
②MA(移動平均)モデル
⇒現在の値は、過去の値の平均値と過去の誤差に影響を受けると考える
モデル
ex.今日の売り上げを「昨日のまで」の売り上げの平均と過去の誤差を
もとに予測する
③ARMA(自己回帰移動平均)モデル
⇒ARモデルとMAモデルを組み合わせたモデル
④ARIMA(自己回帰和分移動平均)モデル
⇒ARMAモデルからトレンド要因を除去したモデル
時系列データを「トレンド要因」と「自己回帰移動平均」に分けて分
析を行う
⑤SARIMA(季節変動自己回帰和分移動平均)モデル
⇒ARIMAモデルに季節変動性を考慮に入れたモデル
季節変動性を持つ時系列データに対応可能
以上の5種類のモデルのうち、①~③のモデルは「定常性」のあるデータのみに対応でき、④・⑤のモデルは「非定常性」のデータにも対応が可能です。
定常・非定常とは時系列分析においてとても重要です。
定常性のあるデータとは、
”時間の経過によらず、一定の値を軸に同じようなふり幅を取るデータ”です。

一方、非定常性のデータとはトレンドや季節変動を持つデータなど、時間によって値が変化していっているようなデータになります。
大体の時系列データは非定常性データであり、これらのデータを何もせずそのまま分析すると分析結果が正しいものではなくなる可能性があります。
そのため、非定常のデータは階差を取ってトレンドを除去したり、季節変動性を考慮したりなどの処理をして定常性のあるデータにする必要があります。
これらの処理をしてくれるのがARIMAモデルやSARIMAモデルとなります。
4.2ARIMAモデルについて
前のチャプターでARIMAモデルはARモデルとMAモデルにトレンド除去を組み合わせたモデルであり、非定常データにも対応可能であると説明しました。
そのため、ARIMAモデルで学習する際はp(自己相関度),d(誘導),q(移動平均)の3つのパラメータを設定する必要があります。
実際にARIMAモデルを構築、パラメータを設定してみたいと思うのですが、このパラメータは手動で設定する必要があるため、総当たりでどのパラメータが適切か判断する方法と情報量基準(モデルの良し悪しを決める指標)を用いて判断する方法があります。
ただ、今回は色々とパラメータを入力して試した結果、エラーが起きず上手くいったパラメータが見つかりましたので、そのパラメータを採用して学習・予測させて見ました。
#ARIMAモデルの構築・学習
model_ARIMA = ARIMA(file_food,order=(1,0,1)).fit()
#予測
pred = model_ARIMA.predict("1960","2020")
plt.plot(file_food)
plt.plot(pred,"m")
plt.xlabel("year")
plt.ylabel("Food self-sufficiency rate(cal)")
plt.show()
#モデルの評価
print(model_ARIMA.bic)
出力結果
284.5939045905285
最初の部分だけ低い打点から始まってしまっていますが、それ以降の部分は良さそうな結果になりました。
また、モデルを評価するBIC(ベイズ情報量基準の略で数値は低いほど良い)の結果も"284"と低い値となりました。
実際のデータと重ねてみましょう。

ARIMAモデルの予測はやや右にずれてしまっているものの、動きの傾向はほぼ同じように見えます。
次に2030年まで予測して見ます。

やや上昇傾向になりました。
少し見にくいので拡大してみます。
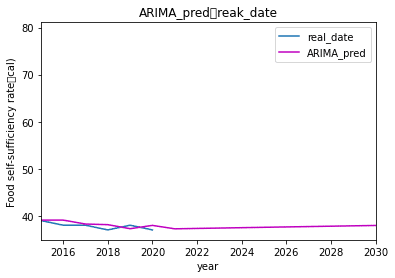
ほんのわずかに微増傾向が見られましたが、ほぼ現状維持という結果になりました。
グラフだと実際の数値がわからないので、数値を見てみます。
#ARIMAモデル
model_ARIMA = ARIMA(file_food,order=(1,0,1)).fit()
#予測
pred = model_ARIMA.predict("1960","2030")
plt.plot(file_food,label="real_date")
plt.plot(pred,"m",label="ARIMA_pred")
plt.title("ARIMA_pred&reak_date")
plt.xlabel("year")
plt.ylabel("Food self-sufficiency rate(cal)")
plt.legend()
plt.xlim("2015","2030")
plt.show()
print(pred.tail(10))
出力結果
2021-01-01 37.233208
2022-01-01 37.313842
2023-01-01 37.394146
2024-01-01 37.474124
2025-01-01 37.553777
2026-01-01 37.633105
2027-01-01 37.712110
2028-01-01 37.790794
2029-01-01 37.869157
2030-01-01 37.947201
Freq: AS-JAN, dtype: float64数値で見ると小数点1桁レベルで微増していたので、やはりほぼ現状維持という結果になりました。
4.3SRIMAモデルについて
次にSARIMAモデルでの学習・予測をしてみます。
SARIMAモデルはARIMAモデルに対して季節変動性も考慮に入れたモデルであると説明しました。
そのためSARIMAモデルはp(自己相関度),d(誘導),q(移動平均)の3つのパラメータに加えて、sp(季節性自己相関),sd(季節性導出),sq(季節性移動平均)の3つのパラメータも加わり、計6つのパラメータを設定する必要があります。
また、このパラメータもARIMAモデル同様、自動で設定する機能はないため、総当たりで探すか情報量基準を用いて選定する必要があります。
ただ、今回はパラメータが6つと多いため、情報量基準とりわけBIC(ベイズ情報量基準)を用いてパラメータを決定していこうと思います。
#パラメータの最適化関数
def selectparameter(DATA, s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs, results.bic)
except:
continue
return parameters[np.argmin(BICs)]
#モデルの構築 (SARIMAモデルの場合)
best_params = selectparameter(file_food,0) #※今回データは季節変動を持たないため、s=0をと設定する
# sm.tsa.statespace.SARIMAXを用いて、file_foodを、selectparameter(file_food,0 )で求めたパラメータが代入された、
best_paramsからorder=best_params[0]やseasonal_order=best_params[1]で取り出してパラメータ設定して、.fit()で学習
#モデルの学習
SARIMA_food = sm.tsa.statespace.SARIMAX(file_food, order=best_params[0],
seasonal_order=best_params[1],
enforce_stationarity=False, enforce_invertibility=False).fit()
#予測
pred_SARIMA = SARIMA_food.predict("1960","2020")
#データの可視化
plt.plot(pred_SARIMA,"g")
plt.show()
#SARIMAモデルのBICを出力
print(SARIMA_food.bic)
出力結果
262.32706993519264
ARIMAモデルの時と同じようなグラフになりました。
BICの数値はARIMAモデルは284、SARIMAモデルでは262とSARIMAモデルの方が低い数値となりました。
次に実際のデータと重ねてみます。

これもARIMAモデル同様、実際のデータよりやや右にずれてしまっているものの傾向は同じような形を取りました。
次に2030年まで予測して見ます。

拡大してみます。

#モデルの構築 (SARIMAモデルの場合)
best_params = selectparameter(file_food,0)
# sm.tsa.statespace.SARIMAXを用いて、file_foodを、selectparameter(file_food, 2)で求めたパラメータが代入された、 #best_paramsからorder =best_params[0]やseasonal_order=best_params[1]で取り出してパラメータ設定して、.fit()で学習
SARIMA_food = sm.tsa.statespace.SARIMAX(file_food, order=best_params[0],
seasonal_order=best_params[1],
enforce_stationarity=False, enforce_invertibility=False).fit()
#予測
pred_SARIMA = SARIMA_food.predict("1960","2030")
# pred_SARIMA_NO = SARIMA_NO.predict("1960","2050")
# print(pred_SARIMA)
#予測したデータと実際のデータを可視化
plt.plot(file_food,label="real_date")
plt.plot(pred_SARIMA,"g",label="SARIMA_pred")
# plt.plot(pred_SARIMA_NO,"c")
plt.xlim(["2015","2030"])
plt.legend()
plt.show()
print(pred_SARIMA.tail(10))
出力結果
2021-01-01 37.0
2022-01-01 37.0
2023-01-01 37.0
2024-01-01 37.0
2025-01-01 37.0
2026-01-01 37.0
2027-01-01 37.0
2028-01-01 37.0
2029-01-01 37.0
2030-01-01 37.0
Freq: AS-JAN, Name: predicted_mean, dtype: float64予測結果もARIMAモデルとほぼ同じになりました。ただ、ARIMAモデルと時と異なり、2020年-2030年の間もずっと37%で数値の増減は見られませんでした。
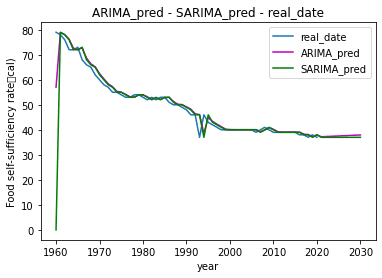
最後に今までのグラフを全て重ねてみます。

Ⅲ.考察・反省
最後に結果の考察と反省をしていきます。
結果として、今回の予測では2030年までの食料自給率は37%とほぼ現状維持という予測となり、目標値である45%には届きませんでした。
このような予測となった要因としては、今回使用したデータが年間データで、月別のデータのように季節変動性を考慮した分析ができなかったことが考えられます。ただ、今回のように年間データしかデータが公開されていない場合は、ARIMAモデル系を利用したデータ分析以外の手法の検討も必要であると考えます。
例えば、食料自給率に、関わる国内での食料生産・消費率や食品の輸出入量・食品廃棄物量などを特徴量として、それらの特徴量から食料自給率を予測するなどの分析方法の方がより精度の高い分析ができ、2020年以降の食料自給率も変化してくると思います。
アイデミーでは1変量のデータを利用したARIMAモデル系の分析手法を学びました。また、今回は、実際にテーマ(目的)の設定からどのようなデータを取得する必要があるか、どのような前処理やモデルが適当かを自分で考え、実行することができました。
まだまだ勉強することがたくさんありますが、今回のようにデータ分析の量を重ね、より学びを深めていけるように精進していきます。
ここまで読んでくださりありがとうございました!
この記事が気に入ったらサポートをしてみませんか?
