2023.10.11『なぜ、算数の授業で子どもが笑うのか？』

【なぜ、算数の授業で子どもが笑うのか？】

→ボケとツッコミが成立しやすいから！？

算数４年「面積」（第1時）

東京都では，習熟度別少人数クラスで学習します。
今回は、したから２番目のクラス。
やる気はあるけど、ゆっくり理解する子が集まっています。
丁寧にボケていきました。
笑いながら、安心して発言する姿を見せてくれました。私自身も楽しかったので、投稿します。

⭐️板書

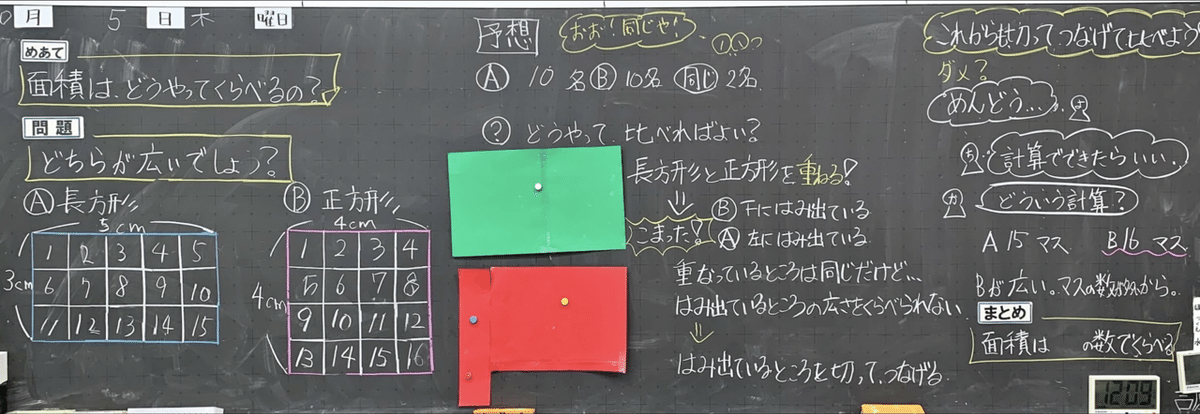
1️⃣課題の設定

「（マスなしで）ＡとＢ、どちらが広いか？」という問題に対して、予想させました。
・Ａの長方形だと思った子が10名。
・Ｂの正方形だと思った子が10名。
・同じ広さだと思った子が２名。
見た目ではわからないことを確認して、「広さをどうやって比べればよいか？」という課題を設定しました。

2️⃣広さを比べる方法を考える

「ＡとＢの広さをどうやって比べればよいか？」、比べ方を考えて、ノートに自分の考えを書かせました。
Ｃ：辺の長さがわかれば、広さがわかるのではないか？
Ｃ：マスを数える！
黒板に薄いマス目があることに気付き、数えたり、面積はたての辺の長さ×横の辺の長さのかけ算で求めたりする子が現れました。
「私は、これは何の式なの〜？わからない〜！どういう意味？なぜ、たて×横をするの？」と投げかけ、ノートに説明を書き加えることを促しました。
直接比較の考え方が子どもたちのノートに見られなかったので、ＡとＢの画用紙をその場で用意し、「先生がしたいことわかる〜？」と発問しました。
Ｃ：わかった！重ねればいいんだ！
Ｃ：でも、重ねても、比べられなくない？
「なんで比べられないのかな？困ったことは、何？」
Ｃ：はみ出るから。
Ｔ「はみ出るからって、どういうこと？」
Ｃ：（前に出て）だから、ＡとＢを重ねると、Ｂは下にはみ出るでしょ？Ａは左にはみ出てしまう。
Ｃ：はみ出るって、そこのことか〜！
Ｃ：はみ出ているところの広さが比べられないから、結局ＡとＢの広さは比べられていない。
Ｔ「なるほど！先生がしたいこと、困っていたことをわかってくれてありがとう！『２つを重ねると、重なっているところは…だけど、はみ出る部分は…。』ということだね！…に言葉を入れて隣の人に説明しましょう。」
Ｃ：（起立し、言えるようになったら座る。全員が座ったことを確認して、ランダムに数名当てる。）
Ｃ：重なっているところの広さは同じだけれど、左にはみ出ているところと下にはみ出ているところの広さを比べられていないから、ＡとＢの広さも比べられていない。
Ｃ：えー？どうすればいいの〜？
Ｃ：わかった！切ればいいんじゃない？
Ｔ「どういうこと？」
Ｃ：切っていいですか？
Ｔ「みんな切るんだって！どう切ると思う？」
Ｃ：わかった！（隣の人に説明したり、ノートに図を描いたり。）
Ｔ「切りたい人いますか？」
Ｃ：（多くの子が挙手）
Ｃ：（ＡとＢを重ね、Ｂの下にはみ出た部分を切る）
Ｔ「ありがとう。切っちゃったよ〜。この切った部分は捨てちゃって、Ａの方が広い！」
Ｃ：いやいやいや！！捨てちゃダメでしょ！
Ｃ：広さ変わっちゃう！
Ｔ：「え？捨てちゃダメなの？じゃあ、切ってどうするの？」
Ｃ：つなげるの！
Ｔ：「つ、つなげる！？どういうこと？わかる人いる？隣の人と話してください。」
Ｃ：（すぐに全員が説明して、座る。）
Ｃ：下にはみ出た部分を切って、左にくっつける！
Ｔ「これで何がわかるの？どう比べるのさ？」
Ｃ：切って、繋げたＢにＡを重ねると、Ｂが飛び出る！
Ｃ：デベソみたい！笑
Ｃ：飛び出た分、Ｂの方が広いってこと！
Ｔ「みんな納得？」
Ｃ：納得〜！

3️⃣今後もそうする？もっと簡単な方法を考える

Ｔ「よーし！広さの比べ方がわかったね！これからも、切って、繋げて比べていけばいいね！」
Ｃ：うん！
Ｃ：いやいやいや…。
Ｔ「何がいやいやいやなの？ダメ？」
Ｃ：ダメ、ダメ！めっちゃめんどう！
Ｔ「めんどうとか言っちゃダメでしょ！がんばりなさい！笑」
Ｃ：いや、そういうことじゃなくて！
Ｃ：先生〜！算数は、『は・か・せ』でしょ？『早く・簡単・正確に』って、〇〇先生言ってたよ！」
Ｃ：簡単な方法じゃないと、間違っちゃう！
Ｔ「なるほど！やる気ないわけじゃないのね？」
Ｃ：ちがう、ちがう！
Ｔ「じゃあ、聞くよ！やる気ないと思ってごめんね。
Ｃ：（笑）
Ｃ：計算すればいい！
Ｃ：計算って、どんな計算するの？
Ｃ：先生、辺の長さ決めていいですか？
Ｔ「あ！確かに！最初に『辺の長さ』って言っていた人いたね。よーし！Ａの長方形は縦の長さが３cmで横の長さが５cm。Ｂの正方形は、縦の長さは４cmね。」
Ｃ：縦の長さは！？
Ｃ：正方形だから一緒でしょ！
Ｃ：そうだったー。
Ｃ：先生、ノートにかいたよ！
Ｔ「なるほど！縦の長さと横の長さがわかれば、長方形も正方形もかけるね。ここの角の角度は？」
Ｃ：90°！
Ｃ：直角！
Ｔ「じゃあ、かいてみて！」
Ｃ：おぉ！ノートすごい！
Ｃ：１、２、３…１５と１６！Ｂが広い！
Ｔ「何、数えているの？」
Ｃ：マス！
Ｃ：ノートのマスが１㎝ぴったりだから、長方形と正方形にマスが重なる！
Ｃ：（マスに線を引く）
Ｔ「おお！それ、黒板でもやって！」
Ｔ「このマスをどうするか、わかる？」
Ｃ：数える！
Ｔ「マスを数えると、Ａが…マスで、Ｂが…マス。」
Ｃ：Ａが１５マスで、Ｂが１６マス。
Ｔ「おお！数えられた！…で？」
Ｃ：「…で？」じゃないのよ！多いんだから広いでしょ！
Ｔ「…ん？」
Ｃ：「…ん？」じゃなーい！Ａが１５マスで、Ｂが１６マスで１マス多いでしょ！だからＢの方が広いの！」
Ｔ「納得？」
Ｃ：納得！納得！
Ｔ「なるほど。面積は…で比べるんだね！自分でまとめを書いて、学習感想を書いてください。」
Ｃ：で、どういう計算なんですか？
Ｔ「確かに！計算でできたらいいって言っていたね！次回、それ考えましょ！」

✅次時もボケます！笑

次回は、今回のまとめから入って、大きさの違うマス目を用意しておいて、普遍単位の必要性と㎠とマスの計算の仕方を学習していきます。
楽しみ✨