日常生活から感じるトポロジー
幾何学は元々測量の必要上から生まれたものだとされていますが、現代ではそうした目的を超えて発展してきた多種多様な幾何学の理論があります。
その中で代表的なものがトポロジー(位相幾何学)です。
トポロジーの話をする前に、中学校で教わるユークリッド幾何学について簡単に思い出しておいた方が良いでしょう。
そこでは三角形たちに対して「合同」や「相似」といった関係を考えました。


ここで重要なのは三角形に対して、合同や相似といった複数の関係を考えることできるという点です。
つまり三角形を同じとみなす自然なやり方にも色々あるということです。
さてトポロジーに話を戻しますが、そこでは図形同士を同じとみなすやり方として「連続変形」を採用します。
これはその図形がゴム膜のような材質で出来ているとして、それを伸ばしたり曲げたりすることを意味します(但し切ったり貼ったりはしません)。
その例として良く挙げられるのがマグカップからドーナツへの連続変形です。
(「数学者はマグカップとドーナツの区別もつかない」というジョークもありますが私は区別できます、よっぽどお腹が空いていなければ!)
トポロジーとはこのように図形を柔らかく考える幾何学なのです。

一方で普通マグカップとドーナツを同じとみなそうと思うことは無いでしょう。
ですから、この例を見てもどうして連続変形できたら同じとみなすということにしたいのかよく分からないかもしれません。
ですがこの連続変形の考え方は誰もが日常生活で自然に使っているものなのです。
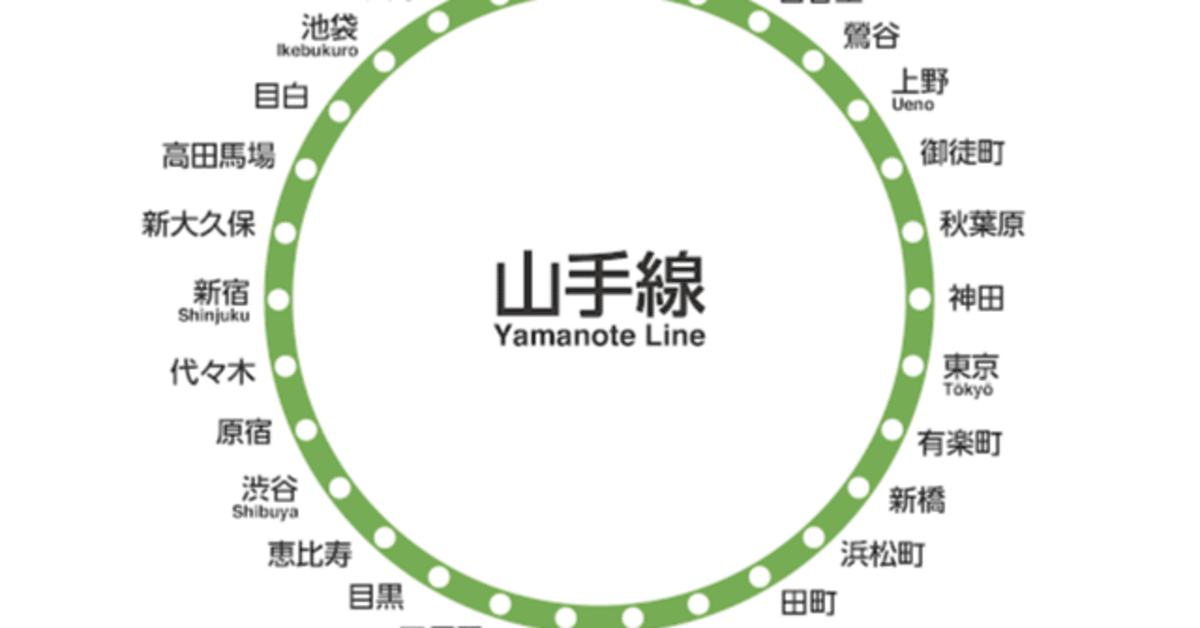
例えば私たちが山手線に乗るとき、その路線図が実際には円ではないことを気にしません。


この場合重要なのは各点(各駅)同士の繋がり方だけであり、その情報さえ保たれていれば上図のように変形しても本質的な情報は失われません。
この変形は連続変形の例だと言えます(上図を輪ゴムのようなものだと思うとイメージしやすいかもしれません)。
一方で、もしどこかを切ってしまって直線のようにしてしまうと駅と駅との繋がり方という本質的情報が損なわれてしまいます。
他の例としては地球があります。
多くの人が地球(の表面)といえば球面を思い浮かべるでしょうが、実際には地球は球面ではなく回転楕円面と呼ばれる類のものです。

一方で、私たちが飛行機に乗るとき地球が実際には球面ではないと意識することはないでしょう。
この場合も重要なのは各都市同士の繋がり方であって、実際の形は問題ではありません。
だから地球を連続変形によって球面だと見なして考えても何ら問題はないわけです。
しかし、もし地球を切って平面にしてしまうと、都市と都市との繋がり方の情報は損なわれてしまうでしょう。
(世の中には地球が平面だと信じている人たちもいるようですが。)
このように私たちは日常でも連続変形という考え方を駆使してそのとき必要な情報を保ちつつ状況を簡略化して生活しています。
この意味で、連続変形という考え方は異なるものを同じとみなす技術として自然なものだと言えます。
トポロジーではこの自然な同一視において不変な量を探し、図形を分類するといった研究が行われてきました。
どういう事か、三角形の例でもう少し説明しましょう。
例えば二つの合同な三角形について、各辺の長さや面積、角度は全く同じです。
ですから合同という関係に対してこれらは不変量であると言えます。
一方二つの相似な三角形について、各辺の長さや面積は必ずしも同じとは言えません。
ですが、角度は依然として全く同じです。
なので相似という関係に対して角度は不変量であるが、各辺の長さや面積はそうでないと言えます。
こうした不変量を定義することはとても有用で、例えば相似な三角形たちは角度によって分類することができます。
特に、異なる角度を持つ二つの三角形は決して相似にはなり得ません。
トポロジーでも三角形に対する角度のような不変量を探す研究が行われ、今日では連続変形に対する不変量として多くの量が知られています。
そのうち最も代表的なものが「ホモロジー群」と呼ばれる量であり、これは20世紀の数学最大の発見の一つだと言ってよいでしょう。
この発見により例えば「球面からドーナツ(浮き輪)への連続変形は可能だろうか?」という問い(直感的にNoだとすぐ分かるでしょう)に対し、球面とドーナツのホモロジー群を計算し、それらが異なることにより厳密にNoだと答えることができます。
ちょうど角度の異なる三角形が相似にはなり得ないように。
ホモロジー群は高度な数学的対象で、正確に説明するのが難しいのですが、それが持つ情報を感じることは依然として可能です。
しかし、もう既にこの記事は長すぎるように思われるので、それはまた別の機会に。
この記事が気に入ったらサポートをしてみませんか?
