Geometry / Γεωμετρία / ज्यामिति / Երկրաչափություն 幾何学
I love geometry #幾何学 in general.
It's a vast theme, and there's no way to provide a decent explanation on this theme in a brief article. Marcel Berger's book on Riemannian geometry entitled "A Panoramic View of Riemannian Geometry" has over 700 pages of text alone and 66 pages for references.
The English adjective "geometric" is frequently used in various contexts, and decently educated people would not have any difficulty in understanding the word albeit possible perversion or abuse.
Honestly speaking, however, I was not good at geometry when I was at junior high school, and that caused my mother, R.I.P.🙏, sent me to a special school...
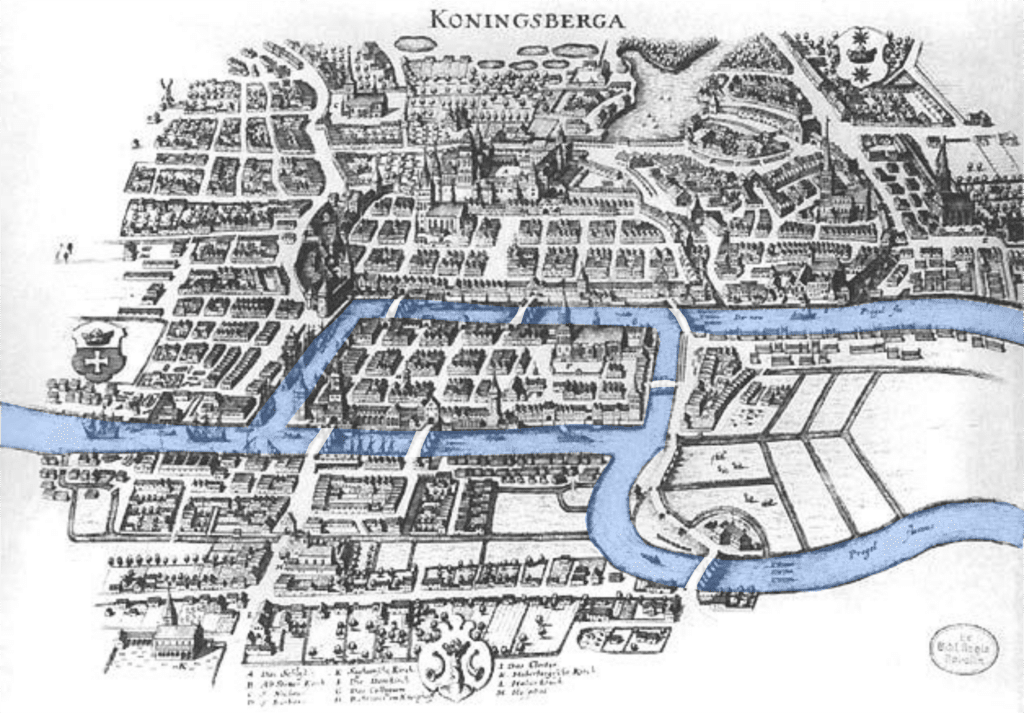
Nevertheless, I had already decided on a mathematics major when I applied to college, and I believe that the Seven Bridges of Königsberg which I had read must have been one key reason why I had chosen mathematics especially Algebraic Topology, a branch of geometry.
(Image below via https://99percentinvisible.org/article/the-seven-bridge-problem-how-an-urban-puzzle-inspired-a-new-field-of-mathematics/ )
As I wrote in my article "Jugendtraum…"
it was highly decisive that I came to know the paper by John Milnor on Homotopy Sphere for me to specialize in Homotopy Theory of Algebraic Topology (代数的位相幾何学), though the area where John Milnor, Michel Kervaire et al. worked as harbingers was called Differential Geometry (微分位相幾何学). Well, I should never skip mentioning René Frédéric Thom, who is very famous with Catastrophe theory but is linked in my mind with Cobordism theory. That is a geometry which has nothing to do with traditional curvature, and also caused me to shift to homotopy theory.
Needless to say it was very exciting to learn Non-Euclidean Geometry (非ユークリッド幾何学) by János Bolyai & Никола́й Ива́нович Лобаче́вский (Nikolai Ivanovich Lobachevsky), however the surprise by the existence of diffeomorphically non-equivalent 7-dimensional spheres was way beyond astonishing.


In the above table, "?" appears for n=3, but that is the famous Poincaré conjecture.
While the story of Sofya Vasilyevna Kovalevskaya I read when I was 15~16 was impressive, somehow, I never felt so interested in specializing in (partial) differential equations. I suspect I was not so much interested in differential equations which appear in physics...much later when I learned the famous story of Perelman's proof for Poincaré conjecture mentioned above, I felt so shocked and cursed my attitude when I was young…
In the institute of technology where I learned, there was some tradition of Differential Geometry (微分幾何学), which I once felt I had better study but soon decided that I should concentrate on Algebraic Topology therefore it was much later that I learned holonomy group. While learning Algebraic Topology, that I read "The Topology of Fibre Bundles" by Norman Steenrod gave me some confidence.
In retrospect it was quite natural that my advisor (a professor) recommended "Topological Methods in Algebraic Geometry" by Friedrich Hirzebruch, surprisingly I did not follow the advice, but determined to study Algebraic Geometry (代数幾何学) from scheme theory. In reality, however, I failed to study this area, which I wrote in the article I mentioned earlier, and I was so glad that I finished reading "Algebraic Geometry and Arithmetic Curves" (by Qing Liu) 44 years after I succumbed to its difficulty of Algebraic Geometry only with superficial understanding of "Algebraic Geometry" (by Robin Hartshorne). Whilst I greatly enjoyed the book by Qing Liu with some difficulties obviously, there're so many topics in Algebraic Geometry yet to learn.
I briefly studied theory of algebraic surfaces (such as famous K3-surface) but not in an exhaustive manner. K3 surface is a beautiful object in Algebraic Geometry, and the following quote by André Weil (1958) is noteworthy:
"Dans la seconde partie de mon rapport, il s'agit des variétés kählériennes dites K3, ainsi nommées en l'honneur de Kummer, Kähler, Kodaira et de la belle montagne K2 au Cachemire."
At this juncture, I don't know whether I will continue to study other topics in algebraic varieties (such as Mori Program) or study another area of geometry…
Although I have not used a very important adjective "projective", there is another geometry called Projective Geometry (射影幾何学), which was once a highly researched area. The famous Erlangen program by Felix Klein published in 1872 as "Vergleichende Betrachtungen über neuere geometrische Forschungen" and the Italian school of Algebraic Geometry were motivated by projective geometry.
[NOTE] Felix Christian Klein (1849-1925) who is famous with the Klein bottle, an example of a non-orientable surface, and Oskar Benjamin Klein (1894–1977) who appears in the Kaluza–Klein theory, are completely different people. The extra dimensions introduced in the Kaluza–Klein theory are curled up and very small, which is essential to string theory.
These days, it is quite often to hear Arithmetic Geometry 数論幾何, which is roughly the application of techniques from Algebraic Geometry to problems in Number Theory, centered around Diophantine Geometry, the study of rational points of algebraic varieties (as per Wikipedia). In reality, it is nothing new.
Here is a brief comparison by Bjorn Poonen extracted from his lecture note "Introduction to Arithmetic Geometry")

What is called "sacred geometry" #神聖幾何学 is completely different from the geometries I have described so far. I appreciate the aesthetic appeal of certain geometric shapes and patterns often associated with so-called sacred geometry, it does not appear to involve any transformation group in terms of Erlangen Program. It's hardly geometry as a branch of mathematics... as a matter of fact, the following Wikipedia entry for geometry does not contain the faintest fragment of the particular word "sacred".
https://en.wikipedia.org/wiki/Geometry
There's a site called "Geometry Code" effectively purposed to promote sacred geometry: https://www.geometrycode.com/sacred-geometry/
Honestly speaking, I am unable to tell what they research under the name of geometry.
Apparently self-contradicting is the following statement in the tutorial:

Wait. A sphere is normally a 2 dimensional manifold (surface) which we visualize in 3-dimensional Euclid space. There is NO center in a sphere.
Incidentally, Fractal Geometry #フラクタル , which is sometimes incorporated into some of the arts, is a proper branch of mathematics.

I have written this article without much context, certainly it was not my intention to just list up various geometries…
I would like to write about some interesting examples in future in another article purely for a record of my study.
2 examples I have in my mind in particular are:
① Klein Quartic, the automorphism group of which is PSL(2,7), the second smallest non-Abelian simple group of order 168.
② The famous example by Heisuke Hironaka for a smooth 3-dimensional complete non projective variety briefly introduced in the textbook by Robin Hartshorne mentioned above. Hironaka's example is so interesting because of offering various perspectives.
Again, it's nothing but a record of my study. In the eyes of professional mathematicians, it would appear nothing more than training for undergraduates... □
この記事が気に入ったらサポートをしてみませんか?
