Jugendtraum - Back to studying mathematics
First of all, I am not a professional mathematician, so what follows is just gibberish by a person who failed to follow the path of the mathematician.
As I briefly mentioned in my first article without any detail, I studied mathematics at a state institute of technology.
When I was 15~16 years old, I could not decide whether I would choose linguistics or study at a university specializing in art & design, and did not have a concrete plan to specialize in mathematics... which tells that I didn't have the foundation to pursue mathematics as a career even though I liked mathematics. It was a stark difference from my classmates of the senior high school, most of whom would study at the University of Tokyo, which is none of my business.
Nonetheless, in 1975 at the 3rd grade at a senior high school attached to a state university, I was determined to pursue mathematics and in the 1st year at the institute of technology in 1976, I was flooded by lots of exciting stories in mathematics, one of which was the "Exotic Sphere" in Differential Topology by John Milnor. That there exist 28 different types of differentiable structures in 7 dimensional spheres sounded so mysterious and attractive:

Contrastingly, Algebraic Geometry, which was known even to laypeople in Japan thanks to Heisuke Hironaka for his winning of the Fields Medal with the magnum opus, did not bring special excitement.
(Later in 2023, I learned the theory of resolution of singularities of algebraic varieties, which is definitely a highly interesting theme in Algebraic Geometry.)
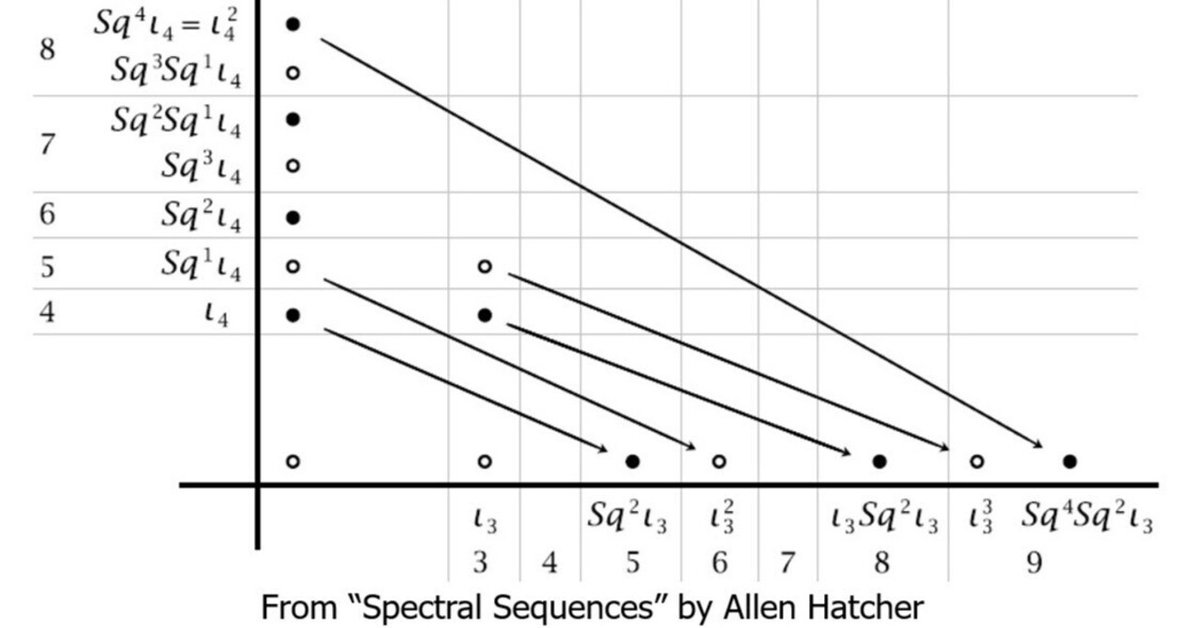
I studied Algebraic Topology very hard in 1978. Then, for a start of my research in 1979, I picked up the paper "On the Non-Existence of Elements of Hopf Invariant One" by John F. Adams:

That an approach by Algebraic Topology resulted in proving non-existence of an algebraic structure was very much appealing, but I felt frosty attitude by class-fellows, senior associates and readers against my choice of such an unappealing (and probably old-fashioned) topic for my study. I would feel a similar frosty reaction at the paper presentation in early 1982. As of writing this note in March 2024, I feel that I suffered from a so-called communication disorder. Perhaps this place should be expressed in the present tense…
In parallel, I studied surgery theory of simply connected manifolds, however, "Surgery of Compact Manifolds" by C.T.C. Wall was way beyond my skill. ("Algebraic and Geometric Surgery" (by Andrew Ranicki) published in 2002 is much more accessible.)
Under the same associate professor, others were reading papers by Dennis Parnell Sullivan and John Willard Morgan.
I still remember that I explained the suspension theorem by Hans Freudenthal in the oral examination in the autumn of 1979 for the graduate school. I must have appeared to be an odd (if not hopeless) student in the eyes of the professors. Evidently it was not a topic that would expand the conversation.
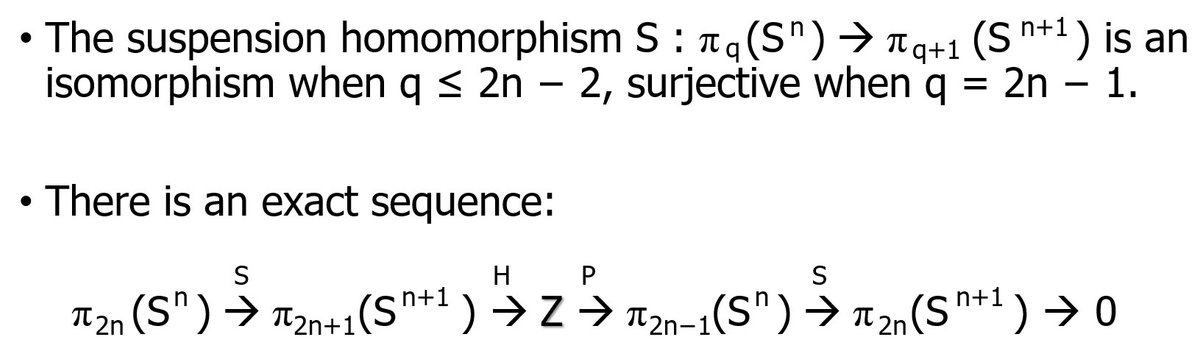
Through my study, I came to realize that Algebraic Geometry was an extremely attractive field of mathematics with ample classic examples. Also interesting is the history of rewriting with Scheme Theory, which can be called a revolution by Alexander Grothendieck. I felt that I would not be able to expect exciting findings in Differential Topology, and decided to pursue Homotopy Theory in Algebraic Topology with a very vague feeling that it would eventually cross with Algebraic Geometry. However, the famous book "Topological Methods in Algebraic Geometry" by Friedrich Ernst Peter Hirzebruch had very little influence on me, although it was strongly recommended by my advisor.
In 1980, I did not make any progress, other than finding myself lost only understanding Algebraic Geometry at superficial level. For a month, I could not concentrate in learning after hitting an "obstruction" while learning Étale cohomology. During such non-productive time, instead I read Russian literature, and I learned that literature of Latin America was so fascinating.
43 years later I felt some achievement in understanding Algebraic Geometry by completing "Algebraic Geometry and Arithmetic Curves" by Qing Liu.

In 1981, I resumed my study in Homotopy Theory. Although my memory is rather vague, Professor Sasao gave a lecture on "groups of self homotopy equivalences", which was rather interesting, and very timely to find a theme to pursue. After participating in a few conferences I acquired some skill from young researchers in calculating the group often denoted as Ξ(X), Ξ (Xi) being the name of the 14th letter of the Greek alphabet, and studying classical techniques developed by Hiroshi Toda, then a professor at Kyōto University, a pioneering researcher in Homotopy Theory, I finally completed my master dissertation titled "On the Groups of Self Homotopy Equivalences of certain CW complexes".

I was very much aware that I was not qualified to continue the path of mathematics and jumped into business in April 1982, and distanced myself from mathematics.
Throughout my learning of mathematics, I did not have any interest in Probability theory and Statistics, which are obviously much more useful in business.
In 2004, while my work was extremely demanding, somehow I started hearing some news about latest development in mathematics, the most significant one of which was the proof of FLT by Andrew John Wiles.

On the other hand, Exotic R4 by Simon Donaldson published just after I left the graduate school, which was much closer to the area I studied, did not excite me for some inexplicable reason, compared to the story of proof of the Poincaré conjecture. Both of the achievements are most definitely important.

In December 2005, coincidentally at the same time of my promotion to a managing director at a Massachusetts based company, I decided that I would resume my study of mathematics after retirement. I had to work 16 years more before being emancipated from extremely demanding job both mentally and physically in October 2021.
After retirement, I resumed my study with review of Number Theory. I was a little pleased to learn the theory of the Brauer group, which I did not feel close to back in 1980. The book by Qing Liu, mentioned earlier, took one year for me to complete.
I'm writing this note knowing that my time is limited with shortness of breath just walking, but I am a little bit confident that I would be able to comprehend the proof of FLT by Andrew Wiles not via popular books for laypeople but through decent understanding of the theories behind his proof. I know it's a lofty goal, but…

この記事が気に入ったらサポートをしてみませんか?
