📏方程式が代数的に解ける ラプラス変換と逆ラプラス変換 ヘヴィサイドも登場
ラプラス変換は微分方程式を解くためのツールであるため、科学や工学の分野で多くの応用がある。
関数 LaplaceTransform(f, s)
入力: f - 時間領域の関数
s - ラプラス変換で使用する複素数変数
出力: F(s) - ラプラス変換の結果
定義: F(s) = ∫(0, ∞) e^(-st) f(t) dt
初期化: 結果を格納する変数 result を 0 に設定
定義: 積分のステップ幅 delta_t(小さい値、例えば 0.01 など)
定義: 積分の上限 approx_upper_limit(理論上は ∞ だが、実際には大きな値、例えば 100 または 1000 など)
// 数値積分 (台形則やシンプソン則などを使用することも可能)
for t から 0 まで approx_upper_limit まで delta_t ずつ増加させる:
// 現在の t での関数の値を計算
current_value = e^(-s*t) * f(t)
// 積分の合計に加算
result = result + current_value * delta_t
return result
線形微分方程式を代数方程式に、畳み込みを乗算に変換する
ラプラス変換は,数学者であり天文学者であったラプラス侯爵 Pierre-Simon, marquis de Laplace にちなんで命名され,彼は確率論に関する研究において同様の変換を用いた.
ラプラスは Essai philosophique sur les probabilités (1814) で生成関数の使用について広範囲に執筆し,ラプラス変換の積分形式は結果として自然に発展している.
ラプラスの生成関数の使用は、現在z変換として知られているものに似ており、彼はNiels Henrik Abelによって議論された連続変数のケースにはほとんど注意を払っていませんでした。 この理論は、Mathias Lerch, Oliver Heaviside, and Thomas Bromwichによって19世紀から20世紀初頭にさらに開発されました。
現在、この変換が(主に工学分野で)広く使われているのは、第二次世界大戦中とその直後のことで、それ以前のHeavisideの操作的微積分を置き換えるものであった。ラプラス変換の利点はGustav Doetschによって強調されており、ラプラス変換という名前はこの人物に由来しているようである。
ラプラス変換は工学や物理学でよく使われます。
ラプラス変換は工学や物理学でよく使われます。線形時不変システムの出力は、その単位インパルス応答と入力信号の畳み込みによって計算できます。この計算をラプラス空間で行うと、畳み込みは乗算になり、後者は代数的な形式であるため解きやすくなる。
ラプラス変換は、多くの関数に対して反転可能である。
システムの入力または出力の簡単な数学的または関数的記述がある場合、ラプラス変換は、しばしばシステムの動作を分析するプロセスや、一連の仕様に基づく新しいシステムを合成するプロセスを簡略化する代替の関数的記述を提供する。
ラプラス変換は微分方程式の解法にも使用でき、機械工学や電気工学で広く使用されている。ラプラス変換は、線形微分方程式を代数方程式に変換し、代数学の正式な規則によって解くことができる。元の微分方程式は、逆ラプラス変換を適用することによって解くことができる。イギリスの電気技術者Oliver Heavisideは、ラプラス変換を用いないものの、同様の方式を最初に提案し、その結果生まれた演算微積分をHeaviside calculus(ヘービサイド微積分)と呼んでいる。
ラプラス変換とその逆変換の広範で一般的な適用性は、天文学のアプリケーションによって説明される。このアプリケーションでは、時間領域とスペクトル(周波数領域)を関連づけるのではなく、点以上として分解するには遠すぎる高周波熱放射の天体源の物質の空間分布に関する情報を、そのフラックス密度スペクトルから得ることができる。
球形で温度が一定であるなどの天体の性質を仮定して、天体のスペクトルに対して逆ラプラス変換を行うことに基づく計算を行うと、天体の中の物質の分布(中心からの距離の関数としての密度)についてスペクトルと一致する唯一の可能なモデルが得られる[36]。天体の構造に関する独立した情報が得られる場合、逆ラプラス変換法は良く一致することが分かっている。
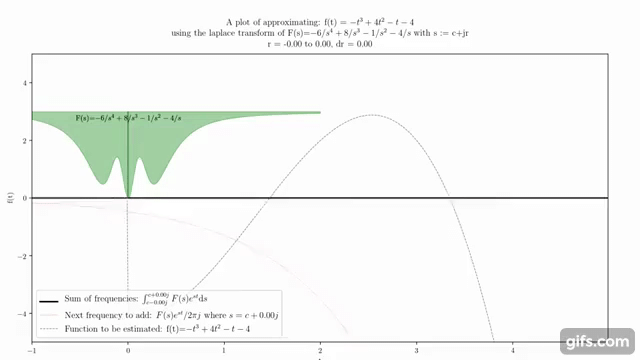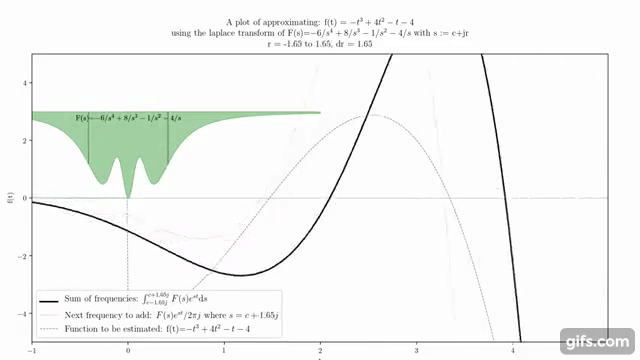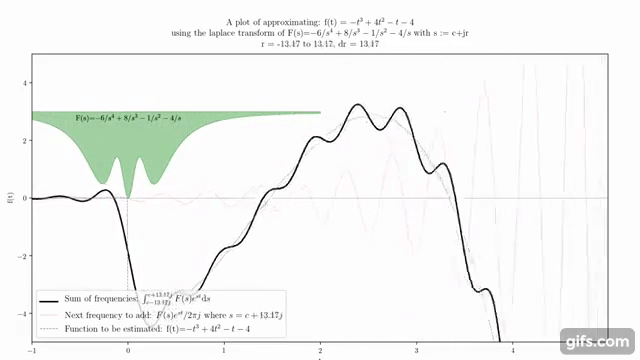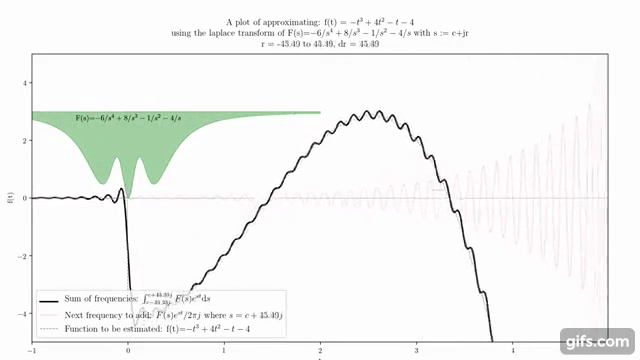
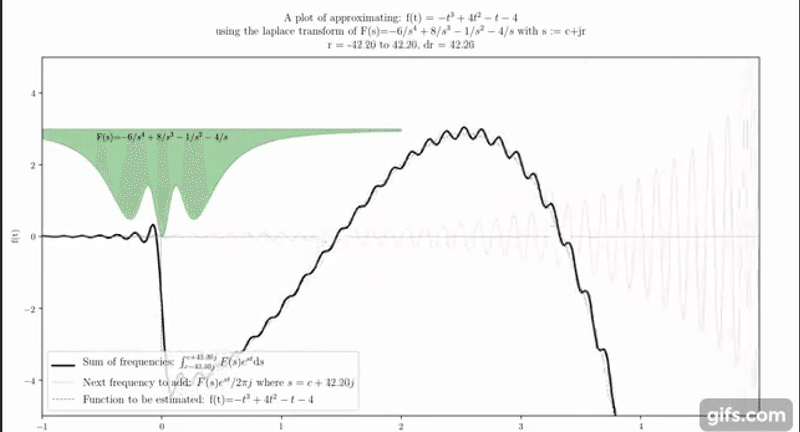
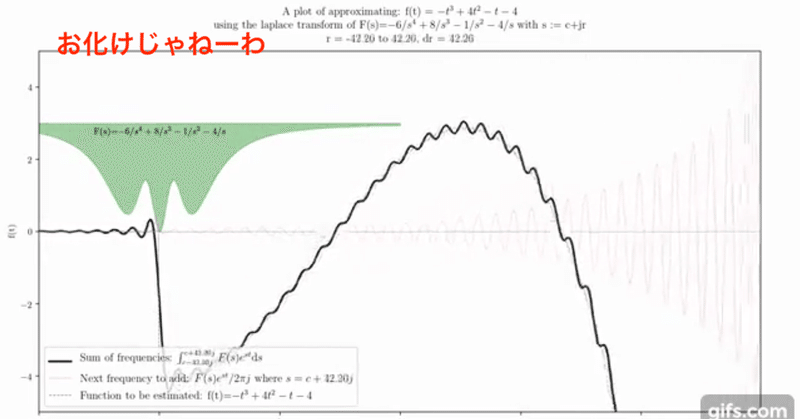
ラプラス変換は、複素関数論と微分方程式の分野で広く用いられる数学的な変換です。この変換は、時間領域の関数を複素周波数領域の関数に変換します。このプロセスは、微分方程式の解析や信号処理など、さまざまな応用において重要です。
「代数的」という言葉がラプラス変換に関連して使われる場合、それは次の点を指します:
代数的操作の単純化:
ラプラス変換は、微分方程式の解法を単純化するために使われます。時間領域での微分演算が、周波数領域でのより簡単な代数的演算(加算、乗算など)に変換されます。代数的手法:
ラプラス変換は、複雑な微分方程式を解くために代数的手法を利用することを可能にします。これにより、解析がより直接的かつ計算が容易になります。
この文脈での「代数的」とは、ラプラス変換が複雑な微分演算をより取り扱いやすい代数的形式に変換する能力を指しています。これは、代数的データ構造が型の合成や組み合わせに関する数学的な原則に基づいていることとは異なる用途です。


これは数値解析では無いですか?
数値解析とは異なります。数値解析は、コンピュータを使用して数値的に近似解を求める手法ですが、代数的解法は方程式の解を具体的な数式で厳密に求める方法です。
代数的解法では、方程式を根号や多項式などの明確な形で解き、解を正確に表現します。これに対し、数値解析では、反復計算や近似式を使って解の近似値を計算します。例えば、ニュートン法や二分法などが数値解析の典型的な手法です。
簡単に言うと、代数的解法は「解の式」を直接提供し、数値解析は「解の近似値」を計算によって求めるのが一般的です。したがって、方程式が代数的に解けるというのは、根号や有限の演算を用いて解を具体的に導出できるということを意味します。
ラプラス変換は五次方程式でも代数的に解けますか?
ラプラス変換は、五次方程式のような多項式方程式を解くために直接使用される方法ではありません。ラプラス変換は主に微分方程式や積分方程式を解く際に用いられる数学的な技術です。これにより、時間領域の方程式をより扱いやすいs領域(ラプラス領域)に変換し、代数的な方法で解を求めることができます。しかし、これは元の微分方程式が線形であり、初期条件が与えられた場合に限ります。
五次方程式などの多項式方程式の解法については、ラプラス変換ではなく他の手法が必要です。五次方程式は、一般にガロア理論により、代数的な解(有理数と根号を使った閉じた形の解)を持たないことが証明されています。そのため、五次方程式の解は代数的手法ではなく、数値解法(ニュートン法やその他の数値的アプローチ)を用いて求める必要があります。
ラプラス変換を五次方程式の解法に適用しようとすると、その方程式が特定の微分方程式から導出される場合に限り有効なアプローチになる可能性はありますが、多項式そのものを直接解く手段としては使用されません。

お願い致します
