
ある1つの時間の矢のパラドックス ~時間反転星に地球から宇宙船が到着する時~
ニュートン方程式やシュレディンガー方程式などの物理学の基礎方程式には時間反転対称性があるので、人間も含めた地球の物質全部の運動を時間反転させたその方程式の解がいつも存在しています。その反転を行った場合には、まるでフィルムの巻き戻しのようにエントロピーが下がる方向へと時間は流れます。しかし人間が意識する時間の矢(時間の向き)自体はエントロピーが増加する方向に時間が流れると感じると考えられます。人間の時間の向きは、人間が記憶する情報が増加する方向になるのが自然だからです。新しいことを学んで、知識、情報が増えるのは「未来」であると自然に感じるためです。
この前提を踏まえると、次のようなパラドックスを考えることができます。ある星の物質全体の運動が地球に対して時間反転をしているとします。地球からその星へ宇宙船を飛ばして着陸させて、その地球人クルーをその星の宇宙人と会話させたり、手を握ったりさせましょう。このとき外部から見ていて、その地球人クルーの時間の矢と、宇宙人の時間の矢の両方が無傷でいられるとは考えられません。ではどちらの時間の矢が反転をして相手の時間の矢に合わせるようになるのでしょう。その星に到着した地球人クルーの時間の向きの感覚はどうなるのでしょう。
物質の量でいうと、その時間反転星の物質のほうが地球からの宇宙船の物質に比べて圧倒的に多いですね。多勢に無勢なので、地球人クルーもやがてその反転星の時間の矢に順応してしまわないのか?その反転星の宇宙人や物体と相互作用をしているうちに、だんだんとフィルムの逆回しではなく、他の宇宙人と同様に普通にエントロピーが増加して見えるように時間が流れているように感じるようにならないのか?それを遠くの地球から観察をするときに、地球の時間の矢と地球人クルーの時間の矢は同じであり続けるだろうか?それとも反転してしまうのだろうか?
この問題の鍵は、やはり地球に残っている観測者からの視点です。宇宙船が到着する前のままの境界条件ならば、その星は地球の時間の矢とは逆の進行をする。でも宇宙船が到着してしまうとその星の境界条件を変えてしまう。たかが宇宙船1機なので最初その影響は小さいが、やがてバタフライ効果でその星全体に影響を及ぼすかもしれない。従って、この地球上の観測者の視点だと、宇宙船の来航を受けたその星全体の時間の矢がやがて地球と同じ方向になっていく可能性もあり得ます。到着した地球人クルーの時間の矢が反転していくのか?それとも、その星全体の時間の矢が反転して地球の時間の矢に近づいていくのか?これこそが「パラドックス」とも呼びたくなる、この問題の本質部分です。
もう1つの鍵は、地球とその星の立場の入れ替えです。これによりパラドックス感が増してきます。時間反転したその星から今度は宇宙人が乗っている別な宇宙船が地球にやってくる場合を考えてみます。その宇宙人クルーが体感している時間の矢は、地球に順応して反転するのかという問いです。またその反転星に残っている宇宙人たちから見て、地球全体の時間の矢がその宇宙船来航のためにやがて反転するのかどうかという問題です。
物理学では通常まず単純化をして問題に取り組みます。そこで地球や星ではなく、図1のように、箱の中を運動するN粒子系を考えてみます。Nは粒子の個数で、普通は圧倒的に大きな数に設定をします。

では図1の運動を、図2のように時間反転させてみましょう。

この新しい時間軸で見ると、図3のようにフィルムの逆回しのように時間が反転して見えます。粒子の速度方向が逆転していることに注意してください。

次に、図4のように初期時刻で孤立している2つのN粒子系を考えます。一方には普通に時間発展する初期状態、他方にはその時間反転運動が起こるように初期状態を設定します。2つの系には相関がないので、このような全体系の初期条件は、まだ原理的には矛盾なく設定できます。

次の設定では、図5のようにこの2つのN体系の重心に運動量を与えて等速直線運動をさせて、ある時刻に重なるようにします。ただ2系の粒子間に相互作用がなければすり抜けてしまうので、右の順時間系と左の逆時間系の運動も時間の矢も特に変更は生じません。

ところがこの2つの系の粒子が力を互いに及ぼすとすると、図6のように状況が大きく変化します。2つの系が重なった時に各粒子は入り乱れて、時間の矢の独立性を保つ条件が壊されてしまいます。外部からこの2つの系の運動を見ている観測者にとっては、やがて2つの系は1つの大きな系に融合します。この時、たとえば高い確率でその大きな系は外部観測者の感覚的な時間の方向に沿う運動(観測者にとってエントロピーが増加して見える方向の運動)を始めるだろうと予想することも可能です。でもこの問題の明確の答えは、まだ与えられていません。

これまでは古典力学で考えてきましたが、量子力学でも同様の問題を考えることができます。初期時刻に図7のような時間反転対称性をもつ状態を設定すればOKです。図7の最初の項が異なる時間の向きをもつ2つの系が重なる寄与を与えています。第2項目ではもう2つの箱はもう重ならないので、エントロピー増加の観点からはその寄与が無視できるようになります。そのため第1項目だけが重要となって、古典力学でのパラドックスと同じ状況が生まれます。この量子力学の問題も、まだ解かれていません。

量子力学ではさらに時間の矢の問題は量子もつれ(量子エンタングルメント)とも深く結びついています。2つのマクロ量子系の間に量子もつれがある状態では、片方だけの部分系の時間反転操作は物理的に存在しないことがわかるからです。量子もつれは部分系の時間の矢の向きを、他の部分系と関係させながら、1つに規定してしまうのです。量子状態は密度行列ρというもので書かれますが、その固有値は一般に非負です。ところが量子もつれ状態で片方の部分系だけに時間反転を行うと、計算で導かれるそのρは負の固有値を持ってしまいます。つまり部分系の時間反転後には、物理的に実現可能な状態にならないのです。その負の固有値の絶対値は量子もつれが強いほど大きくなるため、量子情報理論ではその負の固有値の絶対値の和を、量子もつれの指標としても使っています。
単純なN粒子系ではなく、時間の流れを意識する人間がそれぞれに含まれている順時間系と反転時間系を想定したときには、その内部の人間達の時間の矢は彼らにどのように認識されるかという視点も、問題に新たに加わります。
順時間系と反転時間系を人間とすると、図8になります。左側は男の子の視点での順方向に時間の向きをとってあります。このとき右側のお婆さんがだんだんと若返っていく状態を原理的には作れます。

図8における時間の向きはもちろん人為的であって、図9のように右側の系に合わせる時間軸も採れます。右側の赤ちゃんから観た世界では、左側のお爺さんがだんだんと若返っていきます。

問題は、図10のように時間経過の途中で2人が出会う場合です。その出会いの結果として、2人のそれぞれの生物学的時間の向き、それぞれの感覚の中での時間の矢は修正されてこないでしょうか?これがパラドックス的な問題になります。

なお右側の系から見た風景は図11のようになります。
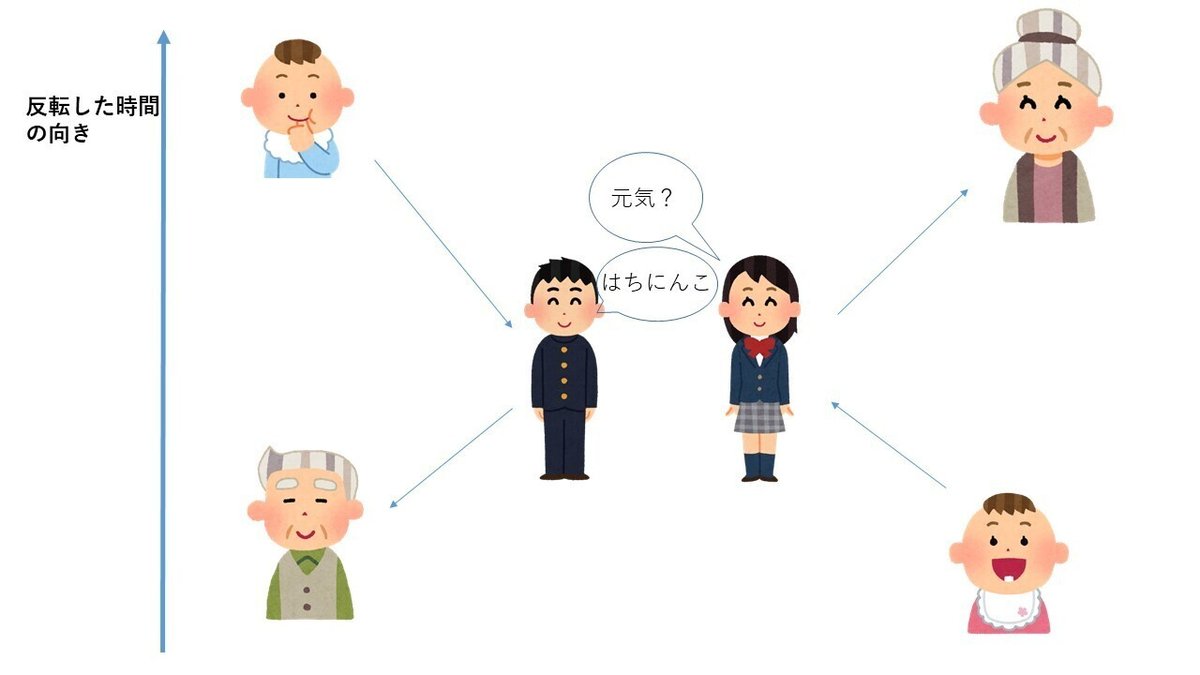
この問題の解も知られていません。ただ1つの仮説として、次のようなことを考えられます。この順時間系と反転時間系の初期状態を用意する外部の観測者が、ケース1として時間反転したお婆さんを準備するのか(図12)、それともケース2として時間反転したお爺さんを準備するのか、どちらの状態を選ぶのかと選択により、その外部観測者にとっての未来の2人の時間が異なる可能性があります。これはこれで尤もらしい仮説だろうと、私は考えています。

外部観測者が時間反転したお婆さんを準備するケース1では、外部観測者の生物的時間を縦軸にとると、2人が会話して相互作用した後に、お婆さんの境界条件が大きく壊れて、再度未来にお婆さんになっていくという可能性です。この場合、男の子も未来にはお爺さんになります。同様に外部観測者が時間反転したお爺さんを準備するケース2では、外部観測者の生物的時間を縦軸にとると、2人が会話して相互作用した後に、お爺さんの境界条件が大きく壊れて、再度未来にお爺さんになっていくという可能性です。この場合、女の子は極普通に未来でお婆さんになります。
外部観測者にとっての時間の向きが、何故反転したお爺さんやお婆さんの時間の向きより優勢なのかという点が、気持ち悪くもありますが、それはやはり「初期状態」というものを準備できる外部の存在が、常に優位な立場であるということかもしれません。とても高い精度で行う観測者によるその状態準備は、飽くまで「観測者にとって」の高精度の微調整となります。だから時間反転したお爺さんやお婆さんの境界条件は、その観測者にとっては簡単に壊れて、観測者と同じ時間の向きに揃っていくという仮説は、それほど悪くないと思います。
私は国際会議のコーヒーブレイクや食事のときに、世界的に著名な研究者たちにもこの問題を質問してみましたが、これまできちんとした回答ができた人はおりませんでした。設定自体は簡単なのに、その答えはまだ誰も知らないという面白い問題です。読者の皆さんも、お暇なときに他の人とこの問題を議論すると大変盛り上がって面白いかなと思います。おすすめです。
いいなと思ったら応援しよう!

