PieceCHECK(2023-23) 最高位2桁の数字

いつもご覧いただきまして、ありがとうございます。KATSUYAです。

お知らせ

拙著シリーズ『Principle Piece 数学B・C～数列～』販売開始しました！

今回の問題

YouTube動画をUPしました。今回は久留米大学(医学部)からで、最高位に関する問題です。

思考時間は5分、目標解答時間はそこから約5分です。

こちらの記事では、動画の中で紹介した解説(答え)を少し丁寧にした答案を、静止画像にて掲載しておきます。

解答

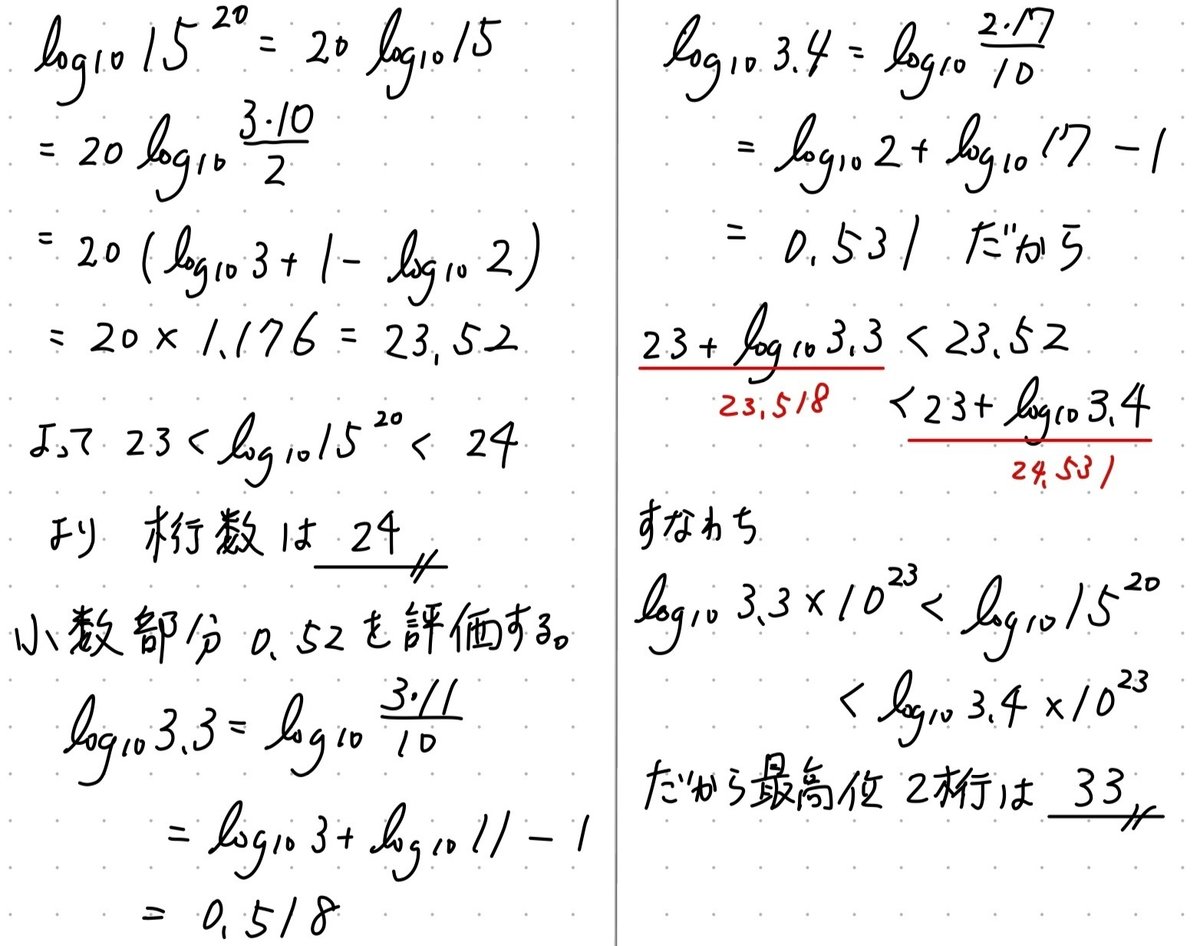
解説・原則など

$${\bm{15^{20}}}$$の桁数と、最高位2桁を求める問題です。
桁数は教科書レベル。15は30/2とみなすと計算しやすいです。

最高位の方がポイント。１桁であれば頻出パターンですが、常用対数の性質をきちんと理解していれば、1桁だろうが2桁だろうが同じ原則ですね＾＾

常用対数の整数部分で桁数を、小数部分で最高位の数を

詳細は拙著シリーズ『Principle Piece 数学Ⅱ～指数関数・対数関数～』p.41を参照

答案にあるように、小数部分は厳しく評価すればするほどより詳しく最高位の情報が得られるということですね。

1桁だけでいいなら、小数部分の0.52を見て0.477$${=\log _{10}3}$$と0.602$${=\log _{10}4}$$の間にあることが分かればOK。もっと詳しく知りたければ、3.1と3.2、3.2と3.3のように、0.1刻みで常用対数を調査して、0.52をはさむ2数を見つけることになります。

与えられている常用対数を見ても、3.3と3.4の間だろうと予想がつくかとは思います。余り本質的ではありませんが、本問は穴埋めでったことと、時間が限られている以上、こういったずる賢さも必要でしょう。

１．解けた人・・・今後の勉強はじっくり演習をしましょう。

２．解けなくて原則を知っていた人・・・拙著『Principle Piece』シリーズで該当するページを熟読し(詳細が書いてあります)、入試演習用の問題集で思考時間を長くする演習をしましょう。

３．解けなくて原則も知らなかった人・・・原則集めからやる必要があります。拙著『Principle Piece』シリーズのような原則習得タイプの問題集で演習しましょう。

Piece CHECKシリーズは、出来あがった答案からは見えない部分を解説していくことで、「なぜそうやって解くのか」「いったいどこからそんな答案が生まれるのか」が分かることを意識して書き上げた参考書です。

関連する拙著『Principle Piece』シリーズ

大手ネットショップBASEでも、デジタルコンテンツとして販売しています。

principle powered by BASE

※ここより先には内容はございません。本記事に価値を感じていただけた方は、ポチっとしていただけると大変うれしいです。(もちろん、任意です)