非常に紛らわしいデシベル(dB, dBFS, dBu, dBv, dBV)という単位
はじめに
音楽経験がそれなりにある人でもデシベルという単位に明るくない人は多いと思います。アンプやエフェクター製作をする人だけでなくPAやレコーディング、DTMをする人でもdB, dBFS, dBu, dBv, dBVの違いやそれらの定義、計算方法を理解していない人は多い印象です。
今回は定義からこれらの違いを理解し、機材の選定や運用、設計に役立てて頂ける内容になっておりますので最後まで是非お読みいただければと思います。
デシベルとは?
デシベルは音楽分野では音圧や電圧の相対値の2乗を常用対数で表したものに10を掛けたものとして定義されます。10を掛けるのは小学校で習ったデシリットル(dL)などで使う接頭語『デシ(d)』をつけ、使い勝手を良くしているからです。なので単位のベル(B)に接頭語デシ(d)をつけたものとして解釈できます。今回は音圧(Pa)については言及せず、電圧(V)を用いて説明していきます。
言葉で説明するとわかりにくいので、基準とする電圧を$${V_{ref} \;\mathrm{[V]}}$$、得られる電圧を$${V\;\mathrm{[V]}}$$、デシベル表記を$${L_V\;\mathrm{[dB]}}$$とおき、式で表すと
$$
L_V=10\log_{10}\bigg(\frac{V}{V_{ref}}\bigg)^2 \;\mathrm{[dB]}
$$
として表されます。ですが、式変形をすることで
$$
L_V=10\log_{10}\bigg(\frac{V}{V_{ref}}\bigg)^2 =20\log_{10}\bigg(\frac{V}{V_{ref}}\bigg)\;\mathrm{[dB]}
$$
が得られます。こうして一般的にデシベルへの変換式として知られている形で表されます。
実用では上式の、基準とする電圧$${\boldsymbol{V_{ref}}}$$をどのような値で定義されているのかが重要になってきます(絶対量としてのデシベル)。
対数(log)について忘れてしまった人や習ったことがない人は適宜以下のサイトを読んでから本記事を読むことをお勧めします。対数のイメージと式変形の方法を理解すると簡単に読み進めることができると思います。
『絶対量としてのデシベル』の各単位の定義と違いについて
dBFS
dBFS(正しくはFSを下付き文字にした$${\mathrm{dB_{FS}}}$$)のFSは『フルスケール(full Scale)』を表します。これはデジタル機材で用いられる単位であり、$${0\;\mathrm{dB_{FS}}}$$をその機材の最大入力レベル、つまり音割れしない限界値を基準としています。$${0\;\mathrm{dB_{FS}}}$$を超えればクリップするので、あと何 dB分ヘッドルームがあるか直感的にわかりやすい単位と言えます。なのでオーディオインターフェイスやデジタルミキサー、その他デジタルエフェクターのインジケーターで用いられることが多いです。
計算式はその機材の最大レベルを$${V_{Max}\;\mathrm{[V]}}$$、入力レベルを$${V_{In}\;\mathrm{[V]}}$$デシベル表記の利得を$${X_{FS}\;\mathrm{[dB_{FS}]}}$$とおくことで、
$$
X_{FS}=20\log_{10}\frac{V_{In}}{V_{Max}}\;\mathrm{[dB_{FS}]}
$$
と表すことができます。
ただし、最大レベルは機材によって異なるため、あくまでその機材内でしか通用しないということは注意する必要があります。
dBu,dBv
dBu,dBvは実は全く同じ定義を持つため、相互に交換可能です。ですが後述のdBVと紛らわしいため、現在はdBuを使うことが推奨されています。ライン機器でよくある+4 dBu(プラヨン)とか-20 dBuとかの単位がこれです。
dBuは
$$
\boldsymbol{\sqrt{600\times{10^3}}}\;\mathbf{[mV_{r.m.s.}]}\boldsymbol{\approx 0.774\,596\,669…}\;\mathbf{[V_{r.m.s.}]}\boldsymbol{\stackrel{def}{=}0}\;\mathbf{[dBu]}
$$
と定義されています。ここで、$${\mathrm{[V_{r.m.s.}]}}$$は電圧の実効値を表しています。
交流信号を扱う場合、示す電圧がピーク値$${\mathrm{[V_{Peak}]}}$$、実効値$${\mathrm{[V_{r.m.s.}]}}$$、ピークtoピーク値$${\mathrm{[V_{P-P}]}}$$のどれであるかを意識する必要があります。サイン波の場合、実効値はピーク値の$${1/\sqrt{2}}$$倍とされており、以下の図のような関係にあります。

ピーク値ではなく実効値で定義される理由はもともとdBuが電力比を示すことに由来し、実効値は電力計算において簡便であるからです。計算の際には実効値とピーク値を間違えないように気を付けましょう。3dBほど計算結果がずれてしまいます。(参考:$${20\log_{10}\sqrt{2}=20\frac{1}{2}\log_{10}2\approx3.0\;\mathrm{dB}}$$)
つまり実効値からdBuを求める式は実効値を$${v_{r.m.s.}\;\mathrm{[V_{r.m.s.}]}}$$、デシベル表記の利得を$${X_u\;\mathrm{[dBu]}}$$とおくことで、
$$
X_u\stackrel{def}{=}20\log_{10}{\frac{v_{r.m.s.}} {\sqrt{600\times{10^3}}}} \approx20\log_{10}{\frac{v_{r.m.s.}} {0.775}} \;\mathrm{[dBu]}
$$
のようになります。また、ピーク値$${v_{Peak}\;\mathrm{[V_{Peak}]}}$$に対しては
$$
X_u \approx20\log_{10}{\frac{v_{Peak}} {\sqrt{2}\times0.775}}\approx 20\log_{10}{\frac{v_{Peak}} {1.10}} \;\mathrm{[dBu]}
$$
と計算してもよいでしょう。
もしくは
$$
\begin{align*}
X_u &\approx20\log_{10}{\frac{v_{Peak}} {\sqrt{2}\times0.775}}\\
&= 20\bigg(\log_{10}{\frac{v_{Peak}} {0.775}}+\log_{10}\frac{1}{\sqrt2}\bigg)\\
&=20\log_{10}{\frac{v_{Peak}} {0.775}}-10\log_{10}2\\
&\approx20\log_{10}{\frac{v_{Peak}} {0.775}}-3.0 \;\mathrm{[dBu]}
\end{align*}
$$
のように式変形することもできます。
dBuから実効値$${v_{r.m.s.}}$$を求める式は上記を式変形することで
$$
v_{r.m.s.}\approx 0.775\times 10^{\frac{X_u}{20}}\;\mathrm{[V_{r.m.s.}]}
$$
という形で得られます。また、ピーク値$${v_{Peak}}$$は実効値の√2倍ですから、
$$
\begin{align*}
v_{Peak}&\approx \sqrt{2}\times0.775\times 10^{\frac{X_u}{20}}\\
&\approx1.10\times 10^{\frac{X_u}{20}}\;\mathrm{[V_{Peak}]}
\end{align*}
$$
という形が得られます。以上の4式があれば計算に困ることは無いでしょう。
dBV
dBVは民生機で用いられる単位のようです。民生機は-10 dBVが基準となっていることが多いです。定義はdBuより単純で
$$
\boldsymbol{1}\;\mathbf{V_{r.m.s.}}\boldsymbol{\stackrel{def}{=}0}\;\mathbf{dBV}
$$
であり、$${1\;\mathrm{V_{r.m.s.}}}$$を基準とします。
このことより、dBVを求める式は、デシベル表記の利得を$${X_V\;\mathrm{[dBV]}}$$とおくことで、
$$
\begin{align*}
X_V&\stackrel{def}{=}20\log_{10}{{v_{r.m.s.}}}\\[12pt]
&=20\log_{10}{\frac{v_{Peak}} {\sqrt{2}}}\\
&\approx20\log_{10}v_{Peak}-3.0\;\mathrm{[dBu]}\\
\end{align*}
$$
と表すことができます。
また、dBuとdBVの関係について、
$$
20\log_{10}\frac{0.775}{1}\approx-2.2
$$
より、
$$
X_V\;\mathrm{[dBV]}\approx X_u \;\mathrm{[dBu]}-2.2
$$
が常に成り立ちます。なので、上記の式を覚えておくことで、暗算で相互に単位変換することができます。
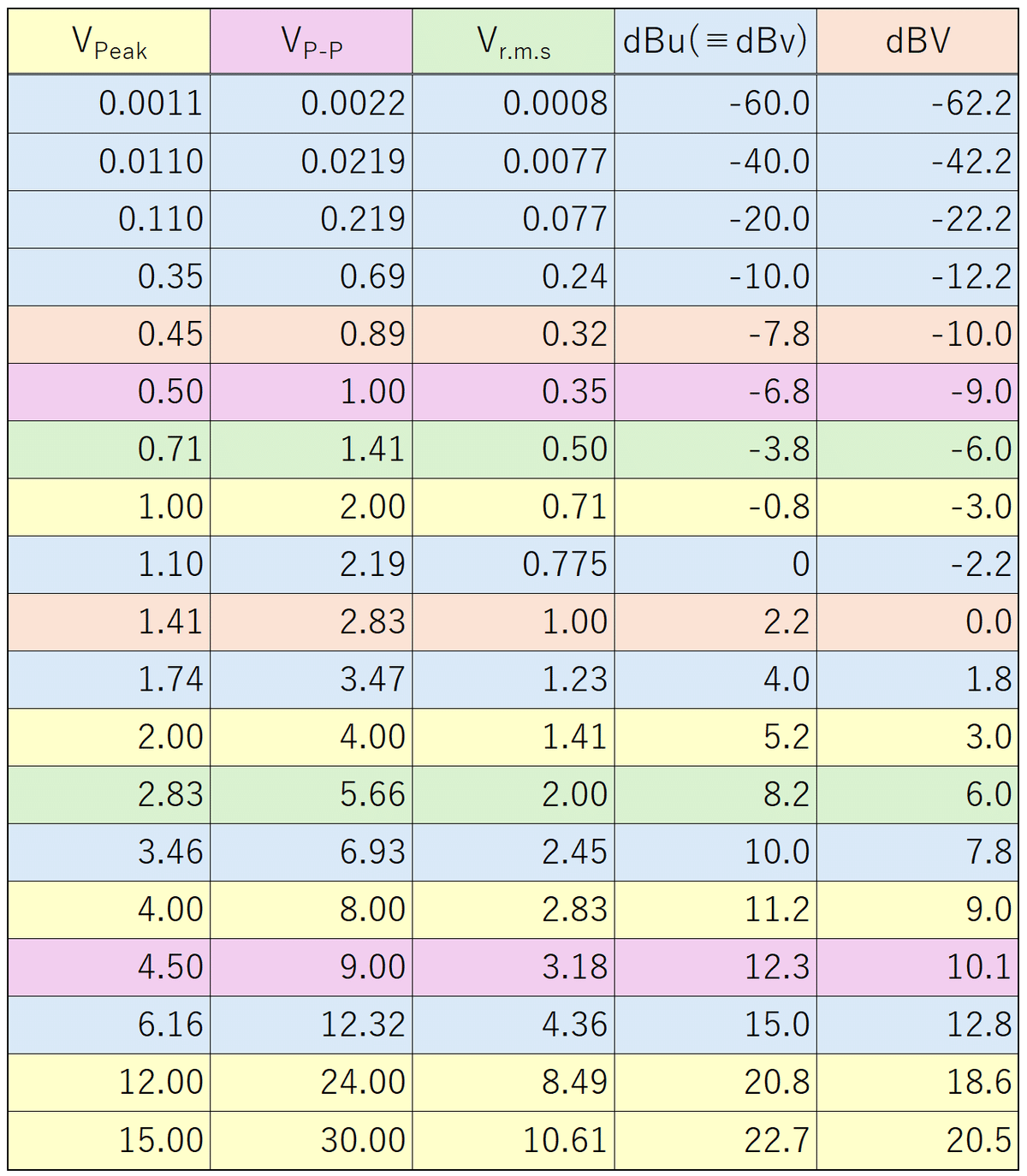
電圧-デシベル変換早見表
設計の時にはそこまで厳密に計算せず、ざっくりとした値が欲しいときがよくあります。毎度計算するのもめんどくさいので表にしてみました。-20dBuや+4dBu、-10dBuなど代表的な値を載せています。是非役立ててください。
最後に
内容自体はかなり数学的なものだと思いますが、エフェクター製作やDTM、PA、レコーディングでは必須知識だと思います。一度で理解できなくても何度も読み返したり、高校数学を復習して、着実に身に着けて頂ければ幸いです。最後までお読みいただきありがとうございました。
追伸
理系学生のクセにTeX(読み方:テフ)に慣れていない所為で半日くらいかかりました。レポート程度だとWordで事足りますが、将来ブログやnoteを書きたい人は勉強しておいた方がいいですよ…(下写真:noteの裏側)

この記事が気に入ったらサポートをしてみませんか?
