
論理学初心者がつまずいた「科学的論理思考のレッスン」
こんにちは。おなつです。
今回紹介する本は『科学的論理思考のレッスン(著:高木敏行)』。
会社の同僚がオススメしてくれた本です。
私は論理学を体系的に学んだことはありません。
論理学は数学と密接に関連しますが、私はコッテコテの文系なのでそういう意味でも縁遠い領域でした。
ですがプロダクトを定義するために、PJを進行するために、論理学の考え方は重要です。私と同じような立場の方にもぜひ論理学に苦手意識なく触れていただければと思い、初学者がつまずいた10個のポイントを挙げていこうと思います。
そしてまず本書は届いてびっくり!本の形が横長なのです。

また、1ページ丸々使ってイラストや図解があるページも多くあります。
いくつになっても、大きい文字かつイラストの多い本は読みやすいです。

本書で紹介している科学的論理思考とは、以下の4つとなります。
①演繹理論
②帰納理論
③アブダクション
④データ科学推論
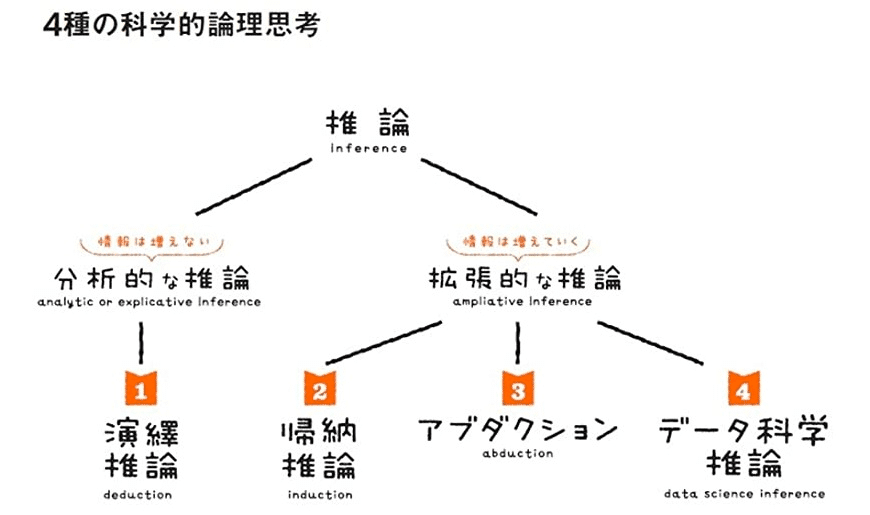
今回はその説明を簡潔にしつつ初心者が間違えたりつまづきやすいポイントを紹介したいと思います。
①演繹推論
演繹推論とは与えられた前提から論理的に結論を導き出すことを言います。
直接推論と間接推論という分類が存在します。
直接推論 = 1つの前提から結論を導く
間接推論 = 2つ以上の前提から段階的に結論を導く
直接推論は以下のような単純な論法になります。
・前提:すべての犬は哺乳類である。
・結論:目の前にいる犬は哺乳類である。
そして間接推論には、定言三段論法、選言三段論法、仮言三段論法といったものがあります。
定言三段論法
定言三段論法 = 前提1と前提2から結論を導き出す推論法
・前提1:すべての犬は動物である。
・前提2:すべてのダックスフンドとは犬である。
・結論:したがって、すべてのダックスフンドは動物である。
前提として動物という集合の中に犬があり、犬という集合の中にダックスフンドがあるという構図。よって結論は自明です。
それでは、以下の推論の誤りがどこにあるか分かりますでしょうか。
・前提1:すべての鳥が飛ぶわけではない
・前提2:ペンギンは飛ばない
・結論:ペンギンは鳥である
前提や結論で表される状態を正しい集合関係で理解する必要があり、ここがまず初心者がつまずきがちなところです。

前提1、2における状態は、ペンギンが右の四角にいるということです。
つまり鳥の中に入るとは限らず、結論は正しいとは言えなくなりますね。
集合関係の整理には、概念をMECEに捉える意識が必要になります。
選言三段論法
「選言」というのは「または」という意味です。(p V q)
選言三段論法 = 「Aまたは、Bのどちらかが真である」という前提から、片方が偽である場合にもう一方が真であるという結論を導く方法
・前提1:スミス氏またはリー氏は弁護士です
・前提2:スミス氏は弁護士ではありません
・結論:リー氏は弁護士です
「または」や「かつ」が登場する論法は論理式でデジタルに考えることができるのですが、ここがまた初心者がつまずきがちなポイントになります。

集合と論理についての処理方法も本書には解説があります。ここでは割愛しますが、日本語で表されるものごとを、( p ∨ q ) のような論理式に変換する意識が必要になります。
仮言三段論法
仮言とは、「もし〜ならば〜」という形式で表される、条件付きの文や命題のことです。(p ⇒ q)
仮言三段論法 = 2つの条件文から新しい条件文を導き出す推論法
前提1: もし犬が走るならば、犬は疲れる。
前提2: もし犬が疲れるならば、犬は眠くなる。
結論: もし犬が走るならば、犬は眠くなる。
ここで初心者がつまづきがちなところは、前提1の仮定が必ずしも真実であると仮定してしまうことです。
例えば、「犬が走っても疲れない場合」や「犬が疲れても眠くならない場合」があります。
このように、仮定が真実であるかどうかを確認しないで仮言三段論法を使うことは、誤った結論を導く可能性があることに注意が必要です。
②帰納推論
帰納推論は、ある条件が何度も繰り返されている場合、その条件が常に成り立つと考える論理の手法です。
帰納推論には枚挙型論証・投射・類推の3種のタイプがあります。
枚挙型論証
枚挙型論証 = たくさんの例を挙げて、その共通点から結論を導く
・根拠1:私の友達のAさんは背が高い
・根拠2:私の友達のBさんは背が高い
・根拠3:私の友達のCさんは背が高い
・根拠4:私の友達のDさんは背が高い
・結論:私の友達は背が高い人が多い
「背が高い」という性質が全員に当てはまることから、「私の友達は背が高い人が多い」という結論を導くことができます。
枚挙型論証は、日常生活やビジネスの現場でよく使われます。
新商品を売り出す際に、過去の成功例や同業他社の事例を列挙することで、その商品の良さを説明することができます。
枚挙型論証では、たくさんの例を挙げることで、その共通点から結論を導き出すことが大切です。少ない例では確証度が低く、全体の傾向を正確に捉えることができません。

投射
投射 = たくさんの例を挙げて、他の例の状態を予測する
・根拠1:犬Aが好きなことはボール遊びだという観察事例
・根拠2:犬Bが好きなことはボール遊びだという観察事例
・根拠3:犬Cが好きなことはボール遊びだという観察事例
・結論:犬Cも、ボール遊びが好きだろう
枚挙型推論が要素全体について予測するのに対し、投射は別の個別要素に対して予測をおこなうものになります。
類推
類推 = 新しい事実を発見するために、類似点を見つけて類推する方法
Aが持っている性質や特徴がBも持っているであろう、という推論
・前提1:私たちが住んでいる地球の周りには、月が回っています。
・前提2:地球と同じように、他の惑星や星の周りにも何かが回っていることが知られています。
このことから、私たちは「宇宙の中で物体は周りに何かを回していることがある」という法則を導き出すことができます。
このように、過去の観測結果から一般的な法則を導き出すことが類推です。
類推においては共通点を見つけることが重要ですが、違いも見逃さずに考慮する必要があります。
枚挙型推論や投射が同じシステム内の全体や別個体について予測をするのに対し、類推は別のシステムへ予測の対象が移ります。
例をいくつか挙げて推論を進めるという形式はどれも同じなので、定義的な分類についても初心者がつまずきやすいところです。
③アブダクション
アブダクション = 「仮説形成」とも呼ばれる考え方の一つで、まだ解決されていない問題や不思議な現象を説明するために用いられる
アブダクションの方法について以下の例をもとに庭の芝生が枯れていた、という例を元に説明します。
問題を明確にする
まず、解決したい問題を明確にします。たとえば、「なぜ庭の芝生が枯れているのか?」という問題を考えてみましょう。仮説を立てる
次に、解決するための仮説をいくつか考えます。たとえば、「水やりが足りていないため」「害虫が発生しているため」「土壌の栄養が足りていないため」などの仮説を考えることができます。仮説を検証する
考えた仮説を検証するために、それぞれについて実験や観察を行います。たとえば、水やりが足りているかどうかを確認したり、土壌の栄養状態を調べたりします。結果を考える
仮説を検証した結果、どの仮説が最も可能性が高いかを考えます。たとえば、水やりが足りていなかった場合は、水やりを増やすことで問題が解決する可能性が高いと判断することができます。仮説を確定する
最後に、最も可能性が高いと判断された仮説を採用して問題を解決することができます。たとえば、水やりが足りていないことが原因だと判断された場合は、水やりを増やすことで庭の芝生を回復させることができます。
ここで初心者がつまづいたり間違えたりしやすいポイントは以下です。
・単一の仮説をすぐに採用してしまう
⇨問題解決において、1つの仮説だけで解決できることは稀です。複数の仮説を考え、それぞれを検証することが重要です。
・仮説を証明するための実験を行わないこと。
⇨仮説を単に考えるだけでは、その仮説が正しいということは分かりません。仮説を検証するために、実験や観察を行うことが必要です。
・既にある結論を逆算してしまうこと。
⇨アブダクションは、新しいアイデアを発見するための手法です。既にある結論を逆算して、それに合わせた仮説を考えることは、アブダクションの本来の目的から外れます。
(余談)仕事で使うなら….
アブダクションは、仕事をおこなう際の問題解決や意思決定において、新しいアイデアを生み出す上で重要な役割を果たします。
例えば、とあるサービスの売上が急激に増加した場合、その原因を探ることが重要です。このような場合にもアブダクションを用いることができます。
まず、増加の原因について仮説を立てます。
例えば、新しい機能の提供により需要が増えた可能性があります。
この仮説を立てたら、その仮説が正しいかを確認するため、顧客調査を行ったり、新機能の利用状況を分析することで、データを収集し検証をします。
もし仮説が正しかった場合、企業は新しい機能を開発することでサービスの売上を増やす戦略を採用することができます。
しかし、仮説が間違っていた場合は、別の仮説を立てて検証を行う必要がありますね。
④データ科学推論
データ科学推論 = 統計学的な手法を用いてデータを活用しておこなう推論
この章ではヒストグラム、代表値、分散と標準偏差、確率分布、統計的推測と検定、相関、順列・組み合わせ・ベイズ推定・リスク分析・誤差・関数が説明されています。
データ科学を使用するには最低限の統計学的知識が必須です。
統計学にはゴリゴリの数式が登場するので、私のような人間には非常に敷居が高く感じてしまいます。
データ科学推論について身近な例で健康について挙げてみましょう。
・健康診断で測定する身長や体重などのデータからBMI(体格指数)を算出し、その値に基づいて肥満や痩せすぎのリスクを推論することができます。
・運動や食事のデータを収集し、それらに基づいて、健康状態の改善や病気の予防に役立つアドバイスを提供することができます。
・健康関連の調査や研究によって得られたデータを分析し、健康問題の原因やリスクファクター(病気の発生や進行の原因となる要素)を特定することができます。例えば、タバコの喫煙ががん発症のリスクを増加させることを推論することができます。
データ科学推論について初心者がつまずきがちな例は、以下のようなものがあります。
1.仮説の正しさを証明することが目的になること。
筋のいい仮説を立てて、分析の結果その通りの定量的な根拠が見られ、進むべき方向性が定まる。ビジネスマンなら脳汁溢れる気持ちの良い瞬間ですが、このシナリオを実現することだけに捉われていけません。
データはあくまで事実であり、そこに解釈を加えることでて次に進むべき道が定まります。仮説の正しさを立証することに捉われると、解釈の部分で歪みが生じうることがあります。
2.相関関係と因果関係を混同してしまうこと
たとえばある研究で、人々が多くのコーヒーを飲むと心臓病のリスクが高くなるという相関関係が見つかったとします。この結果を見て、コーヒーを飲むことが心臓病を引き起こす原因だと考えることがありますが、これは因果関係を混同してしまった例です。
実際には、この相関関係は、コーヒーを飲む人が多い場合に、その人たちが別の要因(タバコを吸う、不健康な食生活など)によって心臓病になりやすいという可能性があることを示しているだけです。つまり、コーヒーを飲むことが直接心臓病を引き起こす原因とはならないということです。
このように、相関関係と因果関係を混同してしまうと、誤った結論を導くことがあります。データ科学推論では、このような誤解を避けるために、注意深いデータ分析と推論をおこなう必要があります。

3.バイアスのあるデータを使って推論すること
例えば、ある小学校が、子どもたちが好きな給食メニューを調べるアンケートを行いました。しかし、アンケートに回答したのは、偏った好みを持つ子どもたちだけでした。
例えば、野菜が嫌いな子どもたちが多く回答した場合、給食に野菜を含むメニューを出すことが少なくなるかもしれません。
このように、アンケートの回答者が偏っている場合、バイアスがあるデータを使って推論をすることになります。そのため、調査対象の範囲を広く取り、多様な人々からの意見を集めることが重要です。
終わりに
論理思考のレッスン、正直私は難しかったです。
データ科学推論の章では確率計算の内容もあり、高校時代に数学からは逃げ切ったと思っていた自分にとっては悪夢のような本でした。
ですが、自分のつまづいてしまうポイント、心当たりのあるポイントなどは全て日常の生活・業務に活かされている部分であることに気づきました。
新しい施策をする際に、アブダクションのように現在の問題を明確にし、仮説を立て、検証できているか。
枚挙型論証のように、たくさんの例を集めることできているか。例えば、多くの顧客からの意見や、市場のトレンドなどを調べ、それらをもとに開発の方向性を考えられているか。
商品を買う際に、偏った商品レビューだけを見ていないか。
また、前回noteで紹介したFACTFULNESS。
これは「事実(データ)をもとに本来の正しい情報を見る習慣をつける」という本でしたが、まさにその礎には今回の内容があってこそだと感じます。
複雑なものごとを考える上での基礎の基礎について、今一度深く潜ってみたい方にとてもおすすめの一冊でした。
さて、ペパボ今年で20周年を迎えました!
この記念すべき年にパートナーとして在籍できること、嬉しく思います。
去年の今ごろ、ホスティング事業部は福岡オフィスのパートナーがほとんどでしたが、現在は本社のある東京オフィスのパートナーも15名に増えました!なんと去年の3倍近く!
また、最南端は鹿児島のメンバーがいます。
採用情報は以下よりご確認ください。ご相談も受け付けております。
以上、おなつでした。
この記事が気に入ったらサポートをしてみませんか?
