お年玉問題

　ポチ袋の中に１円玉が入っています。ポチ袋には円形の穴が貫通しています（表面と裏面の同じ位置に同じ大きさの穴が開いている）。１円玉の直径は20mmで、ポチ袋の穴の直径は15mmです。
　ポチ袋のフタは糊付けされています。ポチ袋を破らずに１円玉を取り出せたら、あなたにあげます。お年玉です。
　ポチ袋を折ったり曲げたりしても構いません。さて、どうやったら１円玉を取り出せるでしょうか。

　この問題をウチの学校の同僚に口頭で出してみました。そうすると数学科の人たちは「できるわけない！」と言うんですね。小さい円形の穴にそれより大きい円板を通すのは不可能だ、と。でも、体育科の人が即答してくれました。頭の中で紙を折ってみて、仕草で「こうやれば通りそうだ」と。数学科の空間認知より、体育科の身体感覚の方が的確だと思った次第です。
　空間図形の問題です。頭の中で考えるだけでは難しいでしょうけれど、実際に紙に穴を開けてあれこれやってみると、そのうちにたぶんポロっと出てきますよ。

　ところで考えてみると、いろんなことをスマホでやるようになって、立体物でも何でもかんでも画面という平面上で認識するようになりました。その際にユーザーが立体感を感じられるように、裏方でクリエイター達が工夫すればするほど、私たちの立体認識能力は落ちていくのかもれませんね。もしかすると、すでにだいぶ落ちているのでしょうか。
　それに対抗するには、リアルに立体物を扱うことが大事。そう、紙に描いて、ハサミで切って、折ってみる、そういう経験を学校でやった方が良いんじゃないか。やってみると、楽しいんじゃないかな。

　ではここで、関連する【問題】をもう１つ行ってみましょう。

紙に空いた直径10cmの円形の穴を通り抜ける円板の直径は、最大で何cmでしょうか？

　ぜひ実際に紙に穴を開けてあれこれやってみてください。たぶん（？）見えてきます。頭の中で考えるだけでは、まず無理（？）でしょうけど。やっぱりリアルな空間でアナログにやってみるのって大事なことだと思うんですよ。バーチャルとデジタルが幅をきかす時代だからこそ。

紙に空いた円形の穴に、それより大きな円板は通るか？

　ポチ袋の中に１円玉が入っています。ポチ袋には円形の穴が貫通しています（表面と裏面の同じ位置に同じ大きさの穴が開いている）。１円玉の直径は20mmで、ポチ袋の穴の直径は15mmです。
　ポチ袋のフタは糊付けされています。ポチ袋を破らずに１円玉を取り出せたら、あなたにあげます。お年玉です。
　ポチ袋を折ったり曲げたりしても構いません。さて、どうやったら１円玉を取り出せるでしょうか。

　空間図形の問題です。頭の中で考えるだけでは難しいかもしれませんが、実際にあれこれやってみると、そのうちにたぶんポロっと出てきますよ。手順を示しましょう。
　まず穴の中心あたりを通る直線状にポチ袋を半分に折ります。この段階ではもちろん１円玉は穴を通りません。（図２）
　次に折り目の両端を手でつまんで内側に押します。力加減と向きを調整しながら押し込むと（図３）のようになります。このとき穴を上から見ると楕円状に見えます。楕円の長軸を長くするには、押し込む向きをやや下向きにするのがコツです。楕円の長軸が１円玉の直径より長くなれば、そこから１円玉がポロっと出てきます。完成です。（図３）

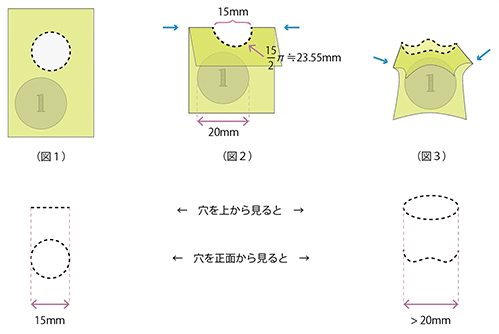
　元の穴の直径 15mm は１円玉の直径 20mm より小さいので、そのままでは１円玉は穴を通りません。でも、穴の周の長さは 15π＝47.1mm で、その半分 23.55mm が１円玉の直径 20mm より大きいので、うまくやれば１円玉は穴を通り抜けられるというわけです。
　なお、穴の曲線の長さはいつも 15π＝47.1mm ですが、（図３）では高さ方向に幅があるので、上から見たときの楕円状の周の長さはそれよりは短くなります。ですから、直径 15π/2＝23.55mm の円板が通るわけではありません。長軸が最大でどこまで長くなるかは別の問題ですが、でも確実に 20mm よりは長くなるので、上の手順で【問題】は解決します。めでたしめでたし。

紙に空いた円形の穴を通り抜ける円板の大きさは？

紙に直径10cmの円形の穴が空いている。紙を破らずになるべく大きな円板を通したい。円板の直径は最大で何cmか。（図１）

　「直径10cmの円形の穴を通り抜ける円板の直径は10cm以下でなければならない」とお考えでしょうか。いや、穴が空いている紙を折ったり曲げたりすれば、直径10cmより大きな円板を通すことができます。
　さて、次に考えるのは「どこまでの大きさの円板なら穴を通り抜けられるか？」です。「紙に空いた円形の穴を通り抜ける円板の直径の最大値はいくつか？」です。

　円形の穴でなく、直径 10cm の円に内接する正方形の穴が空いていると考えましょう（図２）。なぜそう考えるかというと、この正方形の穴は円形の穴より小さいですが、それら２つの穴を通る円板の大きさの最大値が結果として同じになるからです。そして円形の穴で考えるより、正方形の穴で考えた方が考えやすいからです。この場合、正方形の１辺の長さは 5√2=7.07cm です。
　この紙の２か所をつまんで中に押し込む。（図３）のようにあらかじめ山折り・谷折りに折っておくとやりやすい。このとき紙は立体的な形となり、穴は上に盛り上がってきます。もともと正方形だった穴はひし形になります（図４）。
　さらにつまんだ２か所を押し込むと、やがて正方形がつぶれて（図５）のように一直線状になります。このときの紙の形を横から見ると（図６）のようになります。このときの隙間状の穴は、元々の正方形の１辺の長さの２倍＝10√2=14.14cm となります。すなわち、この正方形の穴を通り抜ける円板の直径は最大で 10√2=14.14cm です。

　元の穴が直径 10cm の円形なら、上と同じように紙を組み立てたときの形を上から見ると（図５）と同じになり、横から見ると（図６）の点線のようになります。この場合も穴を通り抜ける円板の直径の最大値は、先ほどと同じです。
　以上から「紙に空いた直径10cmの円形の穴を通り抜けられる円板の直径の最大値は10√2=14.14cm」です。一般に「円板の直径が穴の円の直径の √2 倍までなら円板は穴を通り抜けられる」ということです。//

◇　　　　　　◇　　　　　　◇

〜 人はなぜ円周率に熱くなるのか？ 〜
▷ 円周率とは？　　　　
▷ お年玉問題　　　　　
▷ 輪切りスイカの原理