行列式は計量であるという話

不定期で更新しているnoteの数学シリーズですが、今回は僕の中で線形代数を学ぶ上で一番理解の難しかった行列式に関して、行列式はどういう特徴を表すものなのかという話をします。もう少し突っ込むと、ベクトル空間の上で計量を行うにはベクトルの内積を利用するのですが、この計量方法は行列式に関連しているものであるという話が本記事の主題です。一見なんの関わりもないように見える内積と行列式ですが、内積が導入された経緯を考え、行列式が表すものを紐解いていきましょう。

この記事はある程度線形代数（ベクトル空間、行列式）を理解しているが、行列式がどういった特徴を表すものなのか未だによく理解できていないという人に向けたものです。よって、ベクトル空間の詳しい話や行列式の存在証明、細かい性質に関する話は割愛して進んでいきます。
なお、この投稿では太字のアルファベット(e.g. x, y)をn-dimベクトルとして扱います。tex形式においても同様です。

内積

内積というとなかなかそのイメージを使むのが難しい印象を受ける人が多いのではないでしょうか。高校数学で習う内積ですが、内積の本質を高校数学の範囲できっちり理解するのはとても難しいことだと思います。
高校数学では

と習いますが、大学の線形代数では

と習うことも頭を混乱させる要因の一つですよね。
一度高校数学での内積の定義を捨て、心機一転、脳内の定義をこっちで上書くわけですが、実際、数Bでの定義と線形代数での内積の定義の関係性をきちんと見出すまでにはそれなりの時間をかけて、線形代数を真面目に勉強する必要があります。

内積がなぜこのように定義されているのかと疑問に思う方も多いと思いますが、その答えとしては「内積をこのように定めると、様々な幾何学的な性質が導出できるから」ということなのでしょう。
この話はこの記事を進めていく上で詳しく話します。しかし、今回のゴールは「内積がどういうものであるか」を話すことではなく、内積を導入したことにより、「行列式がどういった特徴を表す値なのか」を見ていくというものですので、行列式の簡単な復習をしましょう。

行列式

行列式はベクトル空間(V = R^n)上に定義され、行列を入力として実数を返す関数のことです。簡単に定義を復習します。

行列式の定義
A = (a_{ij})をn次正方行列とするとき、Aに対する行列式を次のように定義する。

普段はサラスの公式や余因子展開を使って解いてしまうでしょうが、行列式は本来このような形をしています。まず目に入ってくるσですが、これは置換を表しています。置換を簡単に言語化すると行列の成分どうしの掛け合わせの組み合わせのことです。行列のランクをnとするとn!個のσが存在し、σすべてを集めた集合をS_nで表します。2次元ならS_2, 3次元ならS_3, 4次元ならS_4, 以後.......となります。
その他に見慣れないもとしてsign(σ)があります。signは符号を決定する関数でsignatureの略です。3次以上の行列式を求める際には行列の第i, j行（あるいは列）をn!回繰り返し置換していくのですが、一回の置換につき符号が正負の順番で逆転します。signはその置換の回数の遇奇によって符号を決定するのに利用します。（偶数なら1を奇数なら-1を返します。）signの入力がσとなってるのはこのためです。また、この遇奇の個数はそれぞれn/2個づつあることが知られています。

この定義だけでは心もとないと思いますので、例として2次と3次正方行列に関する行列式を見てみましょう。
2次

3次

実際、それぞれの次元で遇奇の個数が一致し、n!個すべての組わせが出現しています。
このような定義から、行列式とはその行列がもつ量（ボリューム）のようなものであると予想することはできます。行列式の使い道として真っ先に思い浮かぶのはある正方行列に対して逆行列が存在する、つまり可逆であるかを判別するというものだと思いますが、その条件は det(A) ≠ 0 でした。ここでは行列式は行列のボリュームと予想していますからボリュームが0にならないなら可逆と解釈できます。
また、行列式に関して一般的に言われているのは、n次正方行列を構成するn個のベクトルが張る空間の符号付き体積（面積も便宜上体積と言っている）を表すということです。つまり、このボリュームが体積に相当するのだとしたら、ベクトル空間上で計量を行いその値が行列式の値と一致するかを見ればこの説が納得できます。その解釈で話を進めれば、det(A) = 0が意味することは体積がないもの、つまり線であるということが言えそうです。

したがって、以降では2次元、3次元についてその面積と体積を計っていこうと思います。

内積の導入

面積や体積を計っていこうと述べましたが、ベクトル空間にはいくつもの定理や概念を実現するための演算という構造こそ備わっていましたが、計量という構造は備わってません。（ここで計量とは、距離、角、面積、体積といった何かを計ることのできる尺度のことです。）
実際、ベクトル空間で行えるのは変換であり、計量ではないということは線形代数を勉強した方なら分かる事実であると思います。

そこで、計量を行う概念としてベクトル空間に「内積」が導入されました。そして、内積が導入されたベクトル空間のことを計量ベクトル空間または内積空間と呼びます。今回は行列式を計量という側面から見ていきたいので、内積を使うとなぜ計量ができるのかという話を先にします。
まずは、今一度内積の定義をおさらいしておきましょう。

(x, y in R^n)

そして重要なポイントとして内積は次の3つの性質を持ちます。

(1) <x, y>はxについてもyについても線形(双線形)である。すなわち任意のx', y'に対して
<x + x', y> = <x, y> + <x', y>,  <cx, y> = c<x, y>, 
<x , y + y'> = <x, y> + <x, y'>,  <x, cy> = c<x, y>
(2) <x, y>はx, yについて対称である。すなわち <x, y> = <y, x>
(3) x ≠ 0ならば、<x, x> > 0 (正定値性)

ここで、(3)の正定値性によって

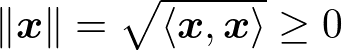
が自然(well-defined)に定義されるのですが、これをベクトルxの長さとし、ノルムと呼びます。このとき、ノルムは次の条件を満たす必要があります。

Xをベクトル空間とする。
(N 1) Xの任意の元xに対して、||x|| ≧ 0 かつ ||x|| = 0となるのは、x = 0 のときのみ
(N 2) Xの任意の元xおよび、任意の複素数aに対して ||ax|| = |a|||x|| が成立
(N 3) Xの任意の元x, yに対し、三角不等式 ||x + y|| ≦ ||x|| + ||y|| が成立

内積から導かれるノルムが(N 1), (N 2), (N 3)を満たすかを調べてみましょう。ノルムの定義より、(N 1)、(N 2)は明らかですね。(N 3)の三角不等式を示します。

三角不等式と距離関数

計量ベクトル空間において、三角不等式を示すにはシュワルツの不等式
 |<x, y>| ≦ ||x||||y||  を示す必要があります。
y = 0またはx = 0 であれば、この不等式は0 = 0で等号が成立しますので、x, y ≠ 0と仮定して証明します。（実際、この不等式は成立するので、証明があまり気にならない人は読み飛ばしてください。）

証明
f(λ) = ||λx + y ||^2  (λ in R) とおく。これを展開すると
f(λ) = <λx + y, λx + y>
       = λ^2<x, x> + 2λ<x, y> + <y, y>
fはλに関する2次式で、すべてのλに対して、正定値性より f(λ) ≧ 0である。
よってa = <x, x>, b = <x, y>, c = <y, y>として判別式D/4 = b^2 - acを取ると、
<x, y>^2 - <x, x><y, y> ≦ 0
したがって、
<x, y>^2 ≦ <x, x><y, y>
が成立する。ここで、正定値性より、両辺とも0以上であるから、両辺の平方根を取り
|<x, y>| ≦ ||x||||y||
を得る。

シュワルツの不等式が成立しましたので、(N 3)の三角不等式を示します。（これも成立しますので、同じく証明が気にならない人は読み飛ばしてください。）

証明
シュワルツの不等式の証明で利用した f(λ) = ||λx + y ||^2  (λ in R)  を再び使う。ここで、λ = 1とおけばシュワルツの不等式により
f(1) = ||x + y||^2
       = <x + y, x + y>
       = <x, x> + 2<x, y> + <y, y>
       = ||x||^2 + 2<x, y> + ||y||^2
       ≦ ||x||^2 + 2|x|||y|| + ||y||^2
       = (||x|| + ||y||)^2
ここで、両辺ともに0以上であるから平方根を取ると
||x + y|| ≦ ||x|| + ||y||
を得る。

内積から導かれるノルムは、ノルムの条件を満たすことが示されました。このことから、このノルムを使ってベクトル空間上に次の距離を導入することができます。

この距離はいわゆるユークリッド距離と呼ばれるもので、高校数学で習う2点間の距離の公式をn次元に一般化したものです。（※距離にも成立のための条件がありますが、内積が定義されたベクトル空間ではシュワルツの不等式が成立するため、この条件は直ちに満たされます。）

ベクトルのなす角

距離が導入されたので、角度も同様に考えることができます。高校数学で習う内積の公式を今一度持ち出してみましょう。<x, y> = ||x||||y|| cosθ でしたが、今、角度cosθを知るために

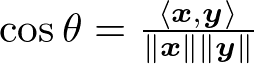
という関係式が導かれます。この右辺はシュワルツの不等式の左辺をシュワルツの不等式の右辺で割って絶対値をとった形になっていることから、-1 ≦ cosθ ≦ 1となることが分かります。（最大値は1となり、絶対値符号を外すことからx, yが負の値をとることがある。）
実際、cosθは-1から1の値を取るので、0 ≦ θ ≦ π が一意的に定まり、この関係式の右辺がcosθに1対1で対応することになります。これをベクトルx, yのなす角といいます。
これが冒頭で言っていた、「内積をこのように定めると、様々な幾何学的な性質が導出できるから」の一つとなります。

2つのベクトルにより張られる平行四辺形の面積を求める

計量ベクトル空間上で距離と角度が使えるようになったので、下図における2つのベクトルa = (a_1, a_2)とb = (b_1, b_2)が張る平行四辺形を考えます。このような面積を内積を用いて求めてみましょう。（分かりやすように、頂点にOABCと名前を付けました。）
図1

以降、\sqrt{ expression }のように、式を\sqrtで囲ったらそれは囲った範囲の式を√内に入れると解釈してください。（大変読みづらいのは承知なのですが、texが使えないのと途中の式だけ画像を差し込んでもかえって見づらいので..）
ここで、AC = ||b||、BC = ||a||です。△OAB = 1/2 ||a|| ・||b||・sinθですので、この平行四辺形の面積 S = ||a|| ・||b||・sinθ であることが分かります。
ここで、
S =  \sqrt{||a||^2・||b||^2 - <a, b>^2}
とも表すことができるのですが、それは次のようにして得られます。

<a, b>^2 = ||a||^2 ・||b||^2 cos^2θ
                 = ||a||^2 ・||b||^2 (1 - sin^2θ)
                 = ||a||^2 ・||b||^2 - ||a||^2 ・||b||^2・sin^2θ
したがって
<a, b>^2 = ||a||^2 ・||b||^2 - ||a||^2 ・||b||^2・sin^2θ
これを変形して
||a||^2 ・||b||^2・sin^2θ  =  ||a||^2 ・||b||^2 - <a, b>^2
両辺の平方根をとり
||a|| ・||b||・sinθ  =  \sqrt{||a||^2・||b||^2 - <a, b>^2}
よって
S =  \sqrt{||a||^2・||b||^2 - <a, b>^2}

これを展開していきましょう。さすがにtexを使います。

最終的に得られた結果から、面積は

と求められました。
しかしこの式、どこかで見たことがありませんか？

やっぱり行列式は平行四辺形の面積だった

上で求めた平行四辺形の面積は実は2次正方行列の行列式

と完全に同じ式となっていたのです。このことから、平面上において、行列式が表すものはやはり2つのベクトルが張る平行四辺形の面積と同じであるということを内積を使って確かめることが出来ました。

さらに面白いのは、内積の性質は行列式の性質にも対応しています。
まずは行列式の性質を確認しましょう。

a_1, .... , a_n ∈ V, A = (a_1, .... , a_n)とする。
D(a_1, .... , a_n) = det(A) = |a_1, .... , a_n|とする。
行列式の性質（この記事で使うもののみ抜粋）
(1) （多重線形性）行列式は各変数a_iに関して線形である。たとえば、a_1に関して
D(a_1 + a_1', ...., a_n) = D(a_1, ...., a_n) + D(a_1', ...., a_n), 
D(ca_1, ...., a_n) = cD(a_1, ...., a_n)

(2)(交代性) 二つの変数a_i, a_j (i ≠ j)を入れ替えると、行列式の符号が変わる。例えば、a_1, a_2, .... , a_n の a_1とa_2を入れ替えたものを
a_2, a_1, .... , a_nとすると、二つの行列式の関係は
D(a_1, a_2, .... , a_n) = -D(a_2, a_1, .... , a_n) 
となる。

内積と行列式の性質の対応
(1)の線形性に関して
例えばベクトルaに対して、k倍するような操作を考えると
\sqrt{||ka||^2・||b||^2 - <ka, b>^2} = k(a_1b_2 - a_2b_1)
と面積もk倍されます。
行列式の多重線形性より、Aの第1列をk倍したA'を作り、その行列式を取ると
det(A') = k(a_1b_2 - a_2b_1)
となり
\sqrt{||ka||^2・||b||^2 - <ka, b>^2} = det(A')
です。
もちろん加法についても同様です。

(2)の対称性に関して
内積に関しては、対称性から
\sqrt{||a||^2・||b||^2 - <a, b>^2} = \sqrt{||a||^2・||b||^2 - <b, a>^2}
となります。
一方行列式に関しては、A = (a, b)とAのaとbを入れ替えた行列をA'' = (b, a)とします。ここでAとA''の行列式を取るわけですが、行列式の交代的な性質を利用することで
det(A'') = -det(A)
とすることができます。

したがって
\sqrt{||a||^2・||b||^2 - <b, a>^2} = -det(A'')
が成立します。

こういった性質を見ていくと、行列式が面積を表すということがより一層理解できます。また、行列式は交代的であったので、符号付き面積と言われている所以も分かりました。

3次元空間ではどうなのか

3次元空間では3つのベクトルが張る空間は平行六面体となります。
図2. 平行六面体の図 (wikipediaより)

平行六面体は立方体ですから、体積 = 底面積 × 高さ で求めることが出来ます。今は計量ベクトル空間を考えていますので、ベクトルを使って体積を測ってみましょう。以下は、見やすいようにベクトルに色を付けてみました。
図3

a = (a_1, a_2, a_3),  b = (b_1, b_2, b_3),  c = (c_1, c_2, c_3) とします。底面積は平面での平行四辺形と同様に
\sqrt{||a||^2・||b||^2 - <a, b>^2}
で求めることが出来ます。
あとは高さがほしいのですが、高さを考えるためにひとつ新たな概念を導入します。それを「外積」といいます。図中でいうと、a × bのピンクの線が外積です。

外積の定義
3次元ベクトルa, bの双方と直交する性質を持つベクトルを

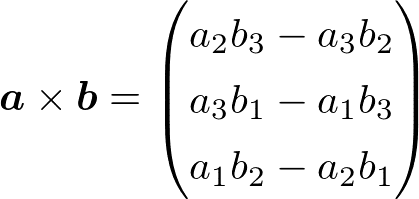
と定義する。

このよう定義になっている理由としては、それはそれで一つ記事がかけるようなボリュームになってしまうのと、本題からそれてしまうので割愛します。気になる方は、外積の大きさについて(新潟工科大学 情報電子工学科 竹野茂治さん著) の解説が非常に分かりやすかったので読んでみてください。

外積を天下り的に導入したところで話を進めていきましょう。直交とは内積が0になることで、<a × b, a> = 0, <a × b, b> = 0 となることを意味します。内積が0になるということは、互いのベクトルが線形独立であることも表します。これを幾何学的に考えると、「a × bはa, b双方に垂直に交わる」となり、まさに上図のピンク色のベクトルに一致します。

外積の性質
(1) aとbに関して交代的である。すなわち
a × b = -b × a
(2) 同じベクトルどうしの外積は0になる。すなわち
a × a = 0
(3) aについてもbについても線形である。すなわち
a × (b +  c) = a × b + a × c,   (ma) × b = m(a × b)

外積のノルム
外積の定義や性質を見てきましたが、外積は内積とは異なり、スカラーではなくベクトルであるということが分かりました。つまり、計量を行うためには外積にも長さ（ノルム）がなければいけないということです。外積のノルムを（がんばって）求めてみましょう。

少し見にくいですが、
||a × b|| = \sqrt{||a||^2||b||^2 - <a, b>^2}
となりました。この右辺どこかで見たことありませんか？そう、これは平面上で２つのベクトルが張る平行四辺形の面積を求めたときの式と完全に一致しているのです。つまり、外積のノルムは元の2つのベクトルが張る平行四辺形の面積と同様であるということが分かりました。よって、行列A = (a, b)の行列式とも一致するということです。

ではこのまま平行六面体の体積を求めます。今一度図3に戻り、平行六面体の高さを考えます。このとき、a × bを底辺としたときに、cが斜辺となる三角形を作ることができるのが見えるでしょうか。ここで、cのa × bに対する正射影を考えると、平行六面体の高さになっており
||c||cosθ
と表すことができます。したがって、これらを平行六面体の体積の公式に当てはめると
v = ||a × b||||c||cosθ = <a × b, c>
となります。なんと今度は体積を内積で表わせてしまいました。これを成分を使って展開すると次のようになります。

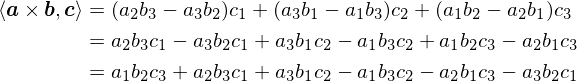
2次元のときと同様に、なにやら行列式のような結果が出てきたと思いませんか？実際に、行列を(a, b, c) として構成し、行列式を求めてみましょう。第1行目(a_j)について余因子展開を使います。

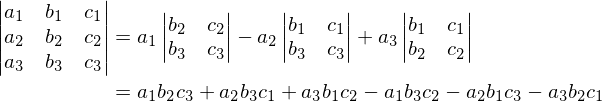
このように、3次元でも同様に行列式は平行六面体の体積と一致しました。
3次元でもやはり行列式は（体積の）計量であったのです。

4次元以上の話

実は、4次元以上でも行列式は計量であるということは変わりません。4次元以上でも面積や体積を一般化したものが考えられ、2次元や3次元同様に内積を利用したアプローチで求めることができるからです。

おわりに

どうでしたでしょうか。行列式は最初に習うときに、ただ計算方法を習うだけで一体何を表しているか理解が難しいと思うのですが、このように計量を用いることで行列式とはどういった値なのかを見ることができたと思います。また、行列式のいくつかの性質も計量であるからこそ備わっていなければいけないものであるということも同時に伝われば嬉しいです。