
【AIって何だろう】ディープラーニングの準備【3/5】
どうも、G検定攻略ガイド管理人です。
第3回のコラムは「ディープラーニングの準備」についてのコラムです。
前々回・前回の記事では「人工知能」「機械学習」のお話をしましたが、今回はその中でも「ディープラーニング」の分野に関する内容です。
本格的なディープラーニングの前に知っておくと理解が深まる内容について詳しくお話をしたいと思います。
前々回・前回記事を読んでいない方は、こちらからどうぞ!
ディープラーニングとは
それでは、ディープラーニングとは何なのか見ていきましょう。

ディープラーニングは「ニューラルネットワーク」を用いた機械学習の手法のひとつです。
ざっくりいうと「学習データをニューラルネットワークに通して学習させモデルを生成する」という感じでしょうか。
順伝播・逆伝播という2方向の演算を行いながら、ニューラルネットワークをチューニングしていき、精度の高い回答が出せるようなモデルを作り上げようという思想の機械学習です。

今回はディープラーニングについて、実際の数学的な解説も付しながら説明をしていきたいと思います。
ディープラーニングは最小二乗法である?
今回は数学的な話が入ってきて、少し嫌な気持ちになる方もいるかもしれません。
ただ、今すぐ全てを理解する必要はありません。何となく流し読んでいただいて、こういう数学的な基盤に支えられた手法なんだということさえ、ふわっとわかればOKだと思っています。
そんなに気張らずに読んでいきましょう!
さて、こんなことがよく言われることがあります。
「ディープラーニングの基本的な考え方は最小二乗法である」
これはあながち間違いではないと管理人は思っています。
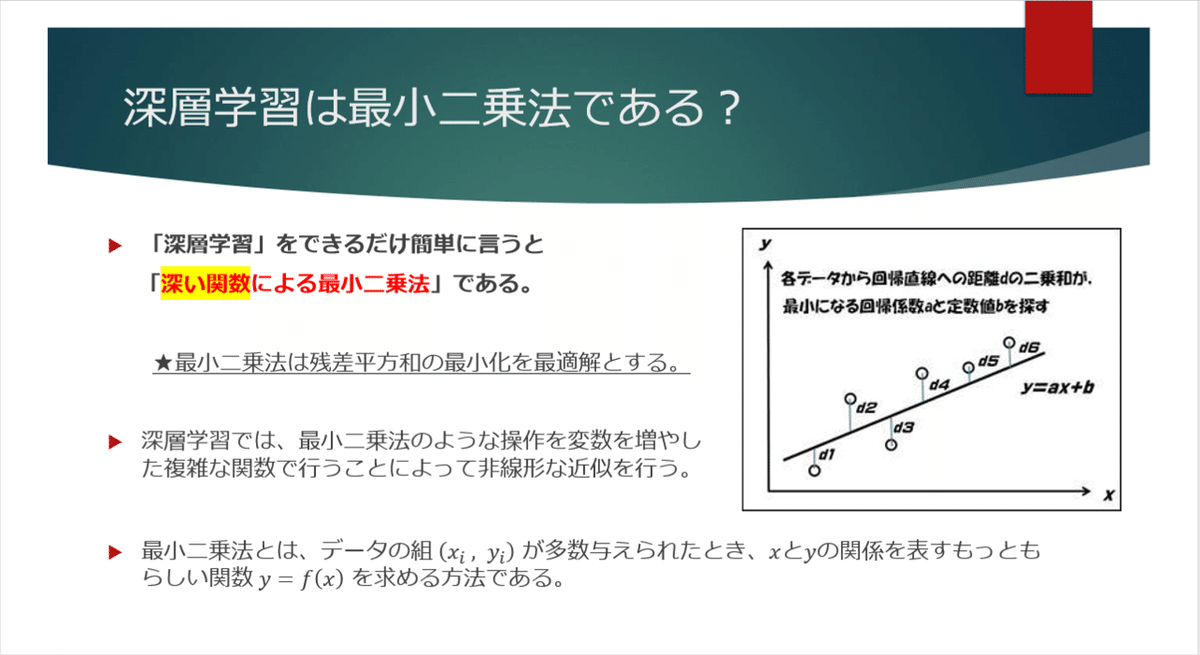
最小二乗法は、エクセルなんかで近似直線を引くようなときにも用いられている手法で、各点からの距離が最も小さくなるように定義した直線を引っ張る手法です。
ディープラーニングでは、最小二乗法をより高次元な空間で非線形関数に近似するという「深い関数による最小二乗法」という表現が適切かもしれません。
参考に、最小二乗法(線形回帰)の数学的解説を付しておきます。


論理回路を見てみよう
今回は数学的な内容が多くて疲れるかもしれませんが、ニューラルネットワークならびにディープラーニングは高度な数学的基盤に支えられた手法です。
できるだけ簡潔に説明しますので、もう少しだけお付き合いください…。
さて、ディープラーニングでは「論理回路」という電気回路の仕組みを図式化したものが登場することがあります。
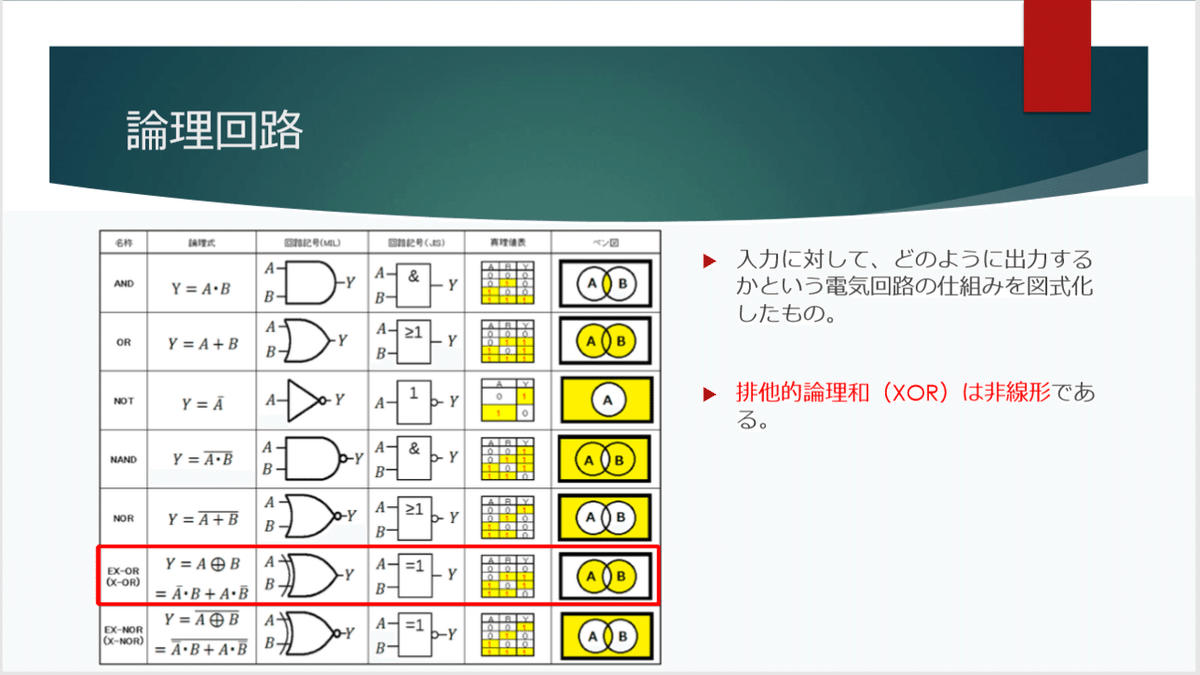
これは全部覚える必要は当然なくて、注目してほしいのは「排他的論理和」というものです。
赤枠で囲んだもの以外は(0,0)(0,1)(1,0)(1,1)の4点をそれぞれYの分類に応じて直線で領域区分することができるのですが、XOR(排他的論理和)だけは「線形分離」が不可能です。
(真理値表をA軸とB軸の二次元平面に書いてみて、直線でYの0,1を区分できる試してみてください…)
論理回路に関しては、ググるといろいろ出てくるので深くは語りませんが、ここでは「ものによっては線形で分離できないやつがある」程度は覚えておいてください。
単層パーセプトロン
さて、ここからはいよいよニューラルネットワークを学ぶ前段階の「単層パーセプトロン」について見ていきましょう。

単層パーセプトロンは、上記の数式で表現できます。
X1,X2という入力に対して、bというバイアスを足しこんだものがaとなり、そのaを活性化関数で処理するという流れになります。
活性化関数は「受け取った値によって振舞いを変えるような関数」です。
たとえばイメージとして下記のような数値が入ってきたとしましょう。
【パラメータ】
X1 = 1 X2 = 2 W1 = 1 W2 = 1 b = 0
【活性化関数】
h(a) = 1(a>=0)
h(a) = 0(a<0)
すると、aは次のように計算できます。
a = 1 ✕ 1 + 2 ✕ 1 = 3
ここで活性化関数に通すと、
h(3) = 1
となり、出力としては「1」が得られます。
ここで活性化関数は何をしているかというと「aが0以上のときは1を、それ以外の時は0を出力する」ということになります。
この活性化関数は、われわれが求めたい出力に応じて変えていくことになります。今後、勉強を進めていくと理解できると思いますので、今は深く考えずに読み進めてください…。
さてここで単層パーセプトロンは、先ほどの「論理回路」の排他的論理和は表現できないということに気づくわけです。
単層パーセプトロンの式は線形であるため、非線形な境界を引くことができないからなのです。

次回へ続く
さて、いかがだったでしょうか?
今回は数学的な手法が多く登場して、少し難しかったかもしれません。
管理人も説明が拙い部分が多かったかもしれませんが、そのあたりはご容赦いただければと思います・・・。
より詳しく学びたい方は、様々な本が出ていたり、ほかにもWebで解説している方がいらっしゃるのでググってみてください…。
次回はいよいよ「ニューラルネットワーク」についてお話したいと思います。
G検定攻略ガイドでは「ディープラーニングG検定」の攻略に役立つ情報を発信しています。
下記リンクより、ぜひ別の記事も読んでいただけると嬉しいです。
ここまで読んでいただき、ありがとうございました。
よろしければサポートをお願いいたします。 記事・コンテンツ作成のモチベーションになります。
