小学生の物理

小学生が3人の我が家では、毎朝6時半頃に15分程度の勉強回をやっている。

ジャンルフリーだが、基本的には学校でならないこと、または、まだ習っていないことをやりたいと思っている。

なるべく宗教、哲学、倫理、政治、経済など本当は子どもに直結するのに、小学校で避けることに触れたいのだけど、最近は、特に小1の末娘から「物理」のリクエストが多い。

ちなみに昨日は「仏教」、一昨日は「英語」、といった感じである。

参加は強制ではなく、3人とも揃うことは少ない。今日は次男が寝坊した。
他にやりたい事があるから参加しないというともあるし、興味がないジャンルだから聞かないという場合もある。

強制はしないけど、全力で楽しそうにやるもんだから、結果的に途中からでも話に加わってくることがほとんど。

天秤問題

数日前にやった、基本的な天秤問題。

この日は、娘（小1）と次男（小2）の参加だったが、ディスカッションしながら、自分たちで答えを出した。

両端のモーメントが釣り合うというのが、天秤のキーポイントなんだけど、小学校低学年がこの問題を見ると、そうは考えない。（当たり前だけど・・）

どうやって考えたかというと、公園のシーソーを想像して、後ろの方に座ると重くなるということに気がついた。そこで、重さの違いの割合と同じくらい、ぶら下がる位置も違えばいいと考えたようである。

この時点で、直感的に30㎝だと答えたのは次男。だが、どうして30㎝なのかうまく説明はできない。

しばらくすると、900ｇと600ｇは3：2に成っていることに気付く。
算数では比の事なんてまだ習っていないので、実際にはそんな高級な言い方ではなく、「こっちは3がみっつ入ってる、こっちは3がふたつ」という言い方である。

「そうそう、それにゼロが二つあるので900は300が3つ、600は300が二つだね」と導いてやる。

ここでひらめいたのが娘。
重さが3：2に対して、長さがXcm：20cmってことは・・・？ということ気付いたようで、だから30ｃｍなんだということで自分なりに納得できたようだ。

天秤の応用問題

今朝は、長男（小5）と娘（小1）の参加。次男は寝坊。

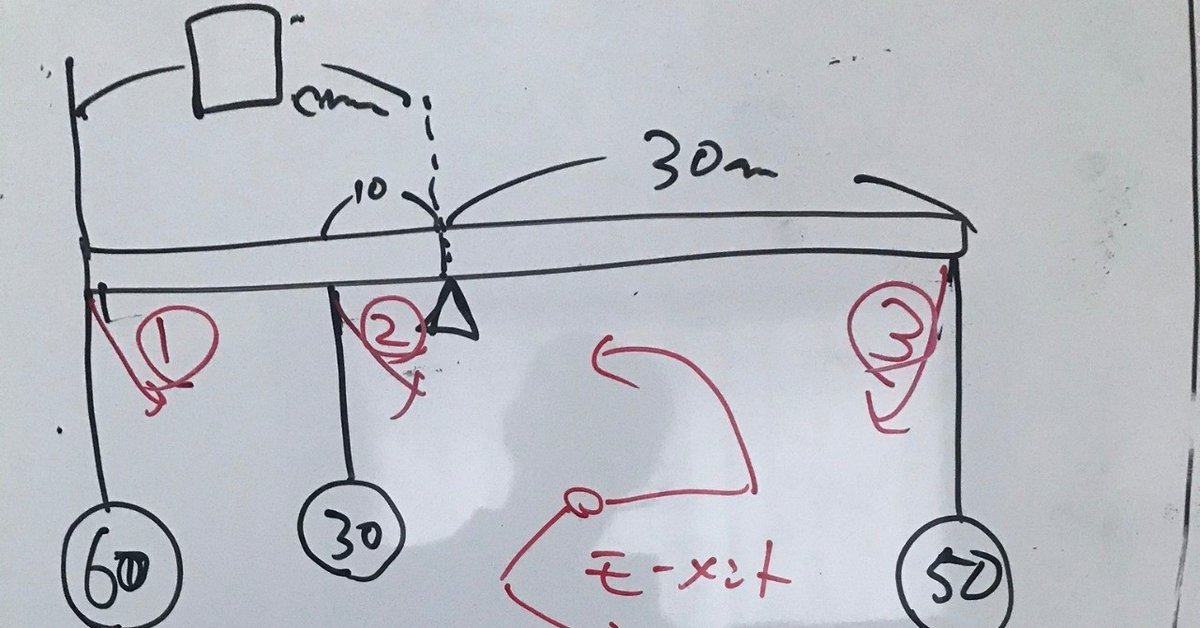
先日の応用で、左側に二つ重りをぶら下げた。
ちなみに、前回の問題を長男に出したところ、ノーヒントであっさり30㎝と答えた。さすが5年生。どうやって考えたか聞くと、重りが1.5倍だから、軽い方の距離も1.5倍だと思った、と言う。

やはり、直感的にはそういうことである。

まあ、長男の考え方については、小学校の4～5年生で、数直線を使った解き方を使いまくるので、それに毒されている感もある。いや、それも有効な手段なので毒されていると言っては失礼だけど。

力学を学ぶときに大事なのは、リアルな世界とリンクして想像出来ているかということだ。物理が苦手な人もリンゴから手を離したらどうなるかは想像つくのに、紙の上に数字を書かれると急に異次元のように捉えてしまうのではないか。

なので、シンプルな設定で、直感的にわかるところから始め、こういう応用問題を解くときに始めて、理論的な話を持ち出すと、「難しい話」ではなくて「便利アイテム」だと気付くのだ。

例えば今回の問題では、赤ペンで書いた①～③の部分を引っ張る力が左右で釣り合えば良いと考えると小学生でも腑に落ちる。その力をモーメントと呼ぶのはあくまで余談。

そこまで納得できたら、5年生が計算するのは簡単だけど、1年生にとってはやや難しい。答えの数字を出せることが重要なのではなく、どうやったら解けそうか作戦を立てられることが大事なのだ。

この辺で、6時50分。さっさと朝ご飯を食べて支度する時間である。