「算数」と「数学」その３

　中学入試本番前日、もうお仕事もなく暇なので前々から書こうと思っていたちらちら見える漸化式的考え方を用いている問題たちについて書きます。

　はいまずはこの問題を解ける人は解ける範囲でどうぞ！

　（１）は僕が温情で付けました。（２）は問題集に乗ってたりします。実際に生徒たちが解いているのも見ました。（３）はまたあとで触れます。

　（１）５段登ればいいので、｛１，１，１，１，１｝が１通り。｛１，１，１，２｝が４通り。｛１，２，２｝が３通りで答えは８通りです。まあ書き出せますかね。

　（２）これくらい書いちゃえ！という気もしますがちょっとしんどくなってくるかな、と言ったところです。ここで登場するのが冒頭で少し書いた「漸化式的な考え」です。１０段目にいる、ということはその前の状態からの動き方としてありえるのは

①９段目にいて１段登った

②８段目にいて２段登った

の２通りしかありえません。もっと言うと、９段目にいる人はあと１段登るしかないので最後に１段登って１０段目にくるときの登り方は９段目までの登り方と同じになります。８段目にいる人はあと２段登るしかないので最後に２段登って１０段目にくるときの登り方はやはり８段目までの登り方と同じになります。

　つまり、１０段目のことを考えようとしたら結局８段目９段目のことさえ考えればよくなってしまった、ということになります。９段目も８段目と７段目からくるしかない、８段目も…。このように、どの段であっても１個前と２個前によって決まるのが分かります。この問題に限って言えばその２つの和になっています。前２つの和が続いていく、と聞くとなにか心当たりがあるでしょうか。

　０段目を１通りと考えてあげると１段目も１通りで、２段目以降は前２つの和をとればいいですから２段目は２通り、３段目は３通り、４段目は５通り、５段目は８通り（（１）と同じ！）となってこれを繰り返すと１０段目が８９通りになります。うーん、書くにはちょっと大変ですね。

　前の内容と対象の内容の関係を式で書いたものを漸化式と言って高校の数学Bでこれを解くことで前の内容や２個前の内容の情報が必要だったものが何番目かの情報が得られれば目的の内容にたどりつけるようになります。前２個の和でその次を考える数列をフィボナッチ数列と言います。とても有名ですね。このフィボナッチ数列の一般項、何番目か分かればすぐに目標の情報が分かる式を作りたい。その内容が（３）になります。

　（３）は「数列｛a_n｝が以下のような漸化式で表せるときその一般項を求めよ」と書き直せます。ｎは自然数（０より大きい正の整数）でｎ項目を表します。（階段だったらｎ段目です）

えー、これの解き方は高校でやりましょう！（丸投げ）ちなみに特性方程式が無理数を含む解になるので厳密には高校でもやりませんがほぼ同じ要領で解けます。（括弧の問題は有理数解になってとても都合がいいので解けるように一応用意しました。答えは割愛します！）

　解いた結果がこちら！

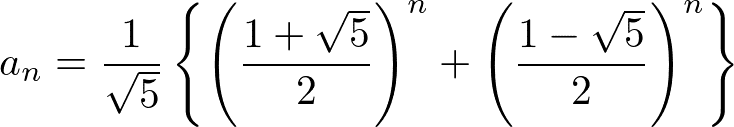
はい。有名かつとても単調な作り方の数列なのに見た感じのいかつさがすごいですね…。どこから出てきたんだその√５は…と思わずつっこみを入れたくなります。この式のｎのところに求めたい段数の数字を入れると下から順に足していくことなく何通りになるか求まります。ちなみに階段の問題は実は１段目が１、２段目が２、から始めているのでこの一般項とはちょっとズレますが話の本質からは外れるのでご容赦ください。

　他にも連立二項間漸化式と呼ぶにはちょっと簡単すぎますがそう呼んでもまあいいかなと思えるくらいのものもありますね。数列や場合の数は中学受験でも頻出単元なので漸化式絡められそうなものも結構多いです。フィボナッチ数列自体もよく出るテーマです。一方大学受験にも、場合の数や確率と絡めて自分で漸化式を立ててその一般項を求める問題が多くあり、漸化式を立てる部分が重要であることも多いです。

　前の情報からどうなっているか、前の情報との関係がどうなっているかをつかむのはそれなりに長い間問われる視点になってきます。こんな考え方する問題もあるよ、それは大学受験までつながる考え方だよ、みたいなことが伝わると嬉しいです。