
AIは連立方程式を、どうやって解くか?
はじめに
皆さん、こんにちは。
今回は、AIに連立方程式を解いてもらうとしたら、どんな風に解くのかについて、説明をさせていただこうと思います。
AIの本懐は自動化
AIが最近、とても流行っていますね。
「AIとは何をしてくれるものか?」と聞かれたら、私は「AIは自動化をしてくれるもの」と答えています。
AIは、自動化の歴史である産業革命の、その第四次の対象としても捉えられています。
INDUSTRY 4.0の技術要素の一つが、AIとなっているのです。
尚、これまでの産業革命で、様々なものが自動化されてきました。
第一次産業革命による軽工業の自動化に始まり。
第二次産業革命による重工業の自動化。
第三次産業革命(IT革命)による書面手続きの電子化。
その都度、社会は豊かになり、人は従来の営みから開放されてきました。
次なる、第四次産業革命によっても、更なる自動化が期待されています。
具体的には、第三次産業革命におけるIT技術では突破できなかった自動化の壁を、「AI ✕ IT技術」によって突破しようとしています。
具体的には、自動運転や、各種自動認証(顔、指紋、etc…)、自動識別(検査、etc…)等々が挙げられます。
AIは机上の空論から脱してきている
AIによる自動化については、AIの下位概念である機械学習を用います。
特に、人間の考える行為を、コンピューター上で実現しようとするのが、機械学習です。
関係性を図示すると、以下のような形です。
自動化に関しては、機械学習を用いて、物理現象の法則性を探索・発見することで実現します。
物理現象の法則性は、過去の実績から、その傾向を分析することで導出します。
それを図にすると、以下のような形になります。
(NY大学にてAIを学んだ友人が教えてくれた、素晴らしい図)

例えば、迷惑メールのデータが沢山蓄積されていたとしたら、それらから迷惑メールの法則性を導出します。
そして、その法則性を、第三次産業革命的な、従来のシステム構成に搭載すれば、迷惑メール判定が自動で行えるようになります。
尚、機械学習における、法則性の探索はどのように行われているかというと、以下になります。
- 比較的単純な試行錯誤を、コンピューターの計算速度任せに繰り返すことで、探索を実現している
- 一方で、法則性発見への到達を、極力少ない試行錯誤数で実現するための、学問的な工夫が凝らされている
具体的なイメージは後述しますので、先ずは、抽象的な感覚を把握してもらえたらと思います。
前者は、機械学習の力任せな側面です。
AIや機械学習という言葉は、やもすれば万能感を漂わせる響きですが、実は、かなり愚直な計算を積み上げています。
計算速度という長所を活かして、強引に法則性を探索している側面が大きいのです。
その為、非常に高いコンピュータースペックが要求されます。
ここ最近まで、AIが日の目を見なかった理由の1つがそれです。
1世代前のコンピューターでは、計算速度の面で、AI・機械学習が机上の空論であったのです。
それが最近になり、AI・機械学習の実現に足る計算速度を、コンピューターが得始めているという訳です。
後者は、AIの緻密な側面です。
コンピューターの計算速度が向上したとは言え、行き当りばったりの総当り的な探索を実施させたのでは、有限時間内に所望の結果を得ることができません。
探索も、効率的に行う必要がある、或いは、効率的に行う方法論があるのです。
用いられるのは、数学や確率統計や物理学といった、従来より物理現象のシミュレーションに用いられてきた学問です。
古くより積み上げられてきた、人間の知恵です。
それらの考え方を導入したアルゴリズムは、より短い手数にて、法則性の導出が行えることが期待できるものとなります。
例えるならば、AIの実現に必要なものは、ホームランバッターの資質と似ています。
ホームランバッターの資質とは、パワーと技術です。
AIの実現で言えば、パワーがコンピューターの計算速度、技術がアルゴリズムの効率の良さ、になります。
共に存在しないと、実現は難しいのです。
ただし、AIはまだまだ過渡期で、成熟期ではありません。
ホームランを打つのは、そう簡単ではありません。
とはいえ、可能性は高くなってきています。
その為、企業は新たなビジネスチャンスの見つけまいと、それぞれAI適用の可能性を模索している形となっています。
人間負荷と、AI負荷のトレードオフ
先程、AIによる自動化については、コンピューターの計算速度と、人間の知恵とが用いられている、と話しました。
では、具体的に、連立方程式をAIに解いてもらう場合、それはどんな形になるでしょうか。
アプローチとしては、以下の要点があります。
- 人が解く場合と同様のアルゴリズムを、プログラム実装し、それをコンピューターに実行してもらう
- コンピューターの計算速度を駆使して、総当たりで探索する
これは、如何に人間側が頑張ってアルゴリズムを組むか、如何に機械側に探索を頑張ってもらうか、という要点です。
或いは、人が問題の解き方を、AIにどの程度教えてあげるか、というニュアンスでもあります。

ここで少し余談ですが…。
かつて、アインシュタインは、「神はサイコロを振らない」という名言を残したそうです。
これは、全ての物理現象には、何らかの明確な要因があり、偶然性というものは存在しないだろう、という仮説です。
仮に、その仮説が正しかったとして、更に、コンピューターに無限の計算速度を持ち、コンピューター上に無限のデータが保持されていたとしたら。
コンピューターに無限の探索を実施してもらえば、物理現象の法則性探索は、サクッと実現できてしまう形になります。
ある条件に対して、起こり得る結果を集計して、予測することは容易いでしょう。
これは、いわゆる全能という状態と言えるでしょう。
しかし、アインシュタインの仮説の正しさは証明されていませんし、コンピューターの計算速度は有限です。
また、コンピューターに存在するデータは、この世界の物理現象を、ほんの少し切り取った程度しか存在していません。
ビッグデータ、ビッグデータと言われる時代ですが、その言葉は今後の指針であって、現状を表してはいません。
現状としては、まだまだデータが不足しているのが実際です。
多くのデータ解析テーマは、データを集めるところからスタートすることが一般的だったりします。
つまり、全能と言える状態は、まだまだ先の話である訳です。
そういう状況の中では、人間とコンピューターとの歩み寄り、或いは、協力が必要となります。
人間が、極力効率良いプログラムを書けば、AIによる自動化が捗ります。
一方で、人間側の負荷は高くなります。
プログラムの実装量が増えたり、プログラムへのBUG混入リスク低減のためにテストを増やさなければならない為です。
或いは、人間が考えた仕様が、必ずしも最適でない場合もあります。
実データ分析においては、人間の主観がデータ解析の精度を押し上げるケースが多いですが、逆に足を引っ張ってしまうことも有り得るのです。
コンピューターによる自動化の比率を高くすると、人間側の負荷が下がり、かつ、ミス無くデータの解析を行うことができます。
主観にとらわれず、客観的にデータを眺めてもくれます。
しかし、コンピューター任せにし過ぎると、今度は、計算量や計算時間の面で問題が出てきます。
計算がなかなか終わらないのです。
また、コンピューターはワビサビが効きませんので、不毛な思考に陥ってしまうこともシバシバです。
そんな人間とコンピューターの協力の感じを、連立方程式を解くエクササイズを通して、説明をしていこうと思います。
連立方程式を、AI的に解いてみる
それでは、連立方程式を解いてみましょう。
解き方には、例えば、以下のような種類が存在します。
(1)人間と同じ「加減法」にて解く
(2)機械丸任せで解く
(3)機械と人間の工夫のミックスで解く
(4)線形代数の考え方を用いて解く
尚、上記以外にも解き方は沢山あります。
ここで説明させてもらうのは、私が思い付く幾つかです。
連立方程式解法例:(1)人間と同じ「加減法」にて解く
先ず、最も一般的な「加減法」に依る解き方です。
中学校で学ぶ解き方ですね。
それを、プログラムにて実装してみます。
解く問題は、この記事のタイトル画像でもある以下です。

尚、「加減法」については、以下の記事が分かりやすいと思います。
「加減法」で、連立方程式を解くプログラムは以下となります。
# tic, toc refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# numpyを使います
import numpy as np
# [step0] 問題を定義
query = np.array([[4, -3, -9], [3, -7, 17]])
# query = np.array([[4, 2, 2], [4, 5, -7]])
print('--------------------------------')
print('[step0] 問題を定義')
for i in range(2):
print('%2dx + %2dy = %2d' % (query[i, 0], query[i, 1], query[i, 2]))
# 処理時間計測START
tic()
# [step1] xの係数の掛け算を、上下交差で実施し、係数を合わせる
query_org = query.copy()
query[0] = query[0] * query_org[1, 0]
query[1] = query[1] * query_org[0, 0]
print('--------------------------------')
print('[step1] xの係数の掛け算を、上下交差で実施し、係数を合わせる')
for i in range(2):
print('%2dx + %2dy = %2d' % (query[i, 0], query[i, 1], query[i, 2]))
# [step2] 上の式から、下の式を引く
query[0] = query[0] - query[1]
print('--------------------------------')
print('[step2] 上の式から、下の式を引く')
for i in range(2):
print('%2dx + %2dy = %2d' % (query[i, 0], query[i, 1], query[i, 2]))
# [step3] 上の式をyの係数で割って、yを求める
query[0] = query[0] / query[0, 1]
print('--------------------------------')
print('[step3] 上の式をyの係数で割って、yを求める')
for i in range(2):
print('%2dx + %2dy = %2d' % (query[i, 0], query[i, 1], query[i, 2]))
# [step4] 下の式にyを代入して、右辺に移行する
query[1, 2] = query[1, 2] - (query[1, 1] * query[0, 2])
query[1, 1] = 0
print('--------------------------------')
print('[step4] 下の式にyを代入して、右辺に移行する')
for i in range(2):
print('%2dx + %2dy = %2d' % (query[i, 0], query[i, 1], query[i, 2]))
# [step5] 下の式をxの係数を、yを代入して、右辺に移行する
query[1] = query[1] / query[1, 0]
print('--------------------------------')
print('[step5] 下の式をxの係数で割って、xを求める')
for i in range(2):
print('%2dx + %2dy = %2d' % (query[i, 0], query[i, 1], query[i, 2]))
# 処理時間計測END
print()
toc()
プログラムの出力結果は以下となります。
--------------------------------
[step0] 問題を定義
4x + -3y = -9
3x + -7y = 17
--------------------------------
[step1] xの係数の掛け算を、上下交差で実施し、係数を合わせる
12x + -9y = -27
12x + -28y = 68
--------------------------------
[step2] 上の式から、下の式を引く
0x + 19y = -95
12x + -28y = 68
--------------------------------
[step3] 上の式をyの係数で割って、yを求める
0x + 1y = -5
12x + -28y = 68
--------------------------------
[step4] 下の式にyを代入して、右辺に移行する
0x + 1y = -5
12x + 0y = -72
--------------------------------
[step5] 下の式をxの係数で割って、xを求める
0x + 1y = -5
1x + 0y = -6
elapsed time: 0.005586147 [sec]
連立方程式が自動で解かれました。
解くまでにかかった時間は、1秒以下です。
人間が解くよりも、圧倒的に高速ですね。
尚、プログラム冒頭で、連立方程式の問題が定義されていますが、そこを別問題に置き換えても、ちゃんと解くことができます。
ただし、2つの変数が未知である方程式が、2つあるような連立方程式のみです。
式の形式も「ax + bx = c」という形でないとNGです。
さて、こうして、連立方程式の自動回答プログラムが作られた訳ですが、ここで「これは、AIなのか…?」という疑問が湧かないでしょうか?
というのも、問題の解き方は、人間が全て指示をしているためです。
これに関しては、半分YESで、半分NOかなと思います。
AIに関しては、何を自動化するかが、1つの焦点となります。
これまでの産業革命でも自動化は行われてきましたが、AIは第四次産業革命ですので、これまでの産業革命とは、一線を画す自動化が焦点となっています。
そこでの差別化要素は、機械学習です。
つまり、問題を解くための解法アルゴリズムも、機械に考えてもらうことまでを期待します。
解法アルゴリズムを人間が考えて、実装していたのでは、第三次産業革命と同じです。
人間が自動化の仕組みを考えて、システム開発をするという第三次産業革命的な営みになる訳です。
ただ、第三次産業革命的な要素が、第四次産業革命の時代にて一切無くなる訳でもありません。
第四次産業革命の技術が、これまでの技術の上に乗っかってくる感じです。
ですので、そもそもそういう仕分けをすること自体に、あまり意味はなかったりはします。
大事なことは問題が解けることです。
それがどんな風に解かれたかは、二の次かと思います。
ですので、先程紹介したプログラムが、瞬殺で実装できるのであれば、機械学習など用いる必要は無いかと思います。
しかし、実際には、プログラム実装にはそれなりの時間がかかります。
また、問題には条件がありました。
現状のアルゴリズムでは、「ax + bx = c」という形の式が、2つ並んでいるような連立方程式じゃないと解けないのです。
尚、機械学習は、そこを突破できる可能性があります。
次には、その解法例を紹介していきます。
連立方程式解法例:(2)機械丸任せで解く
次は、機械学習を用いた形で、連立方程式の解いてみます。
やろことを先に伝えると、総当たりで答えを探索します。
非常にシンプルな解き方です。
プログラムは以下となります。
# tic, toc refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# numpyを使います
import numpy as np
# [step0] 問題を定義
query = np.array([[4, -3, -9], [3, -7, 17]])
# query = np.array([[4, 2, 2], [4, 5, -7]])
print('--------------------------------')
print('[step0] 問題を定義')
for i in range(2):
print('%2dx + %2dy = %2d' % (query[i, 0], query[i, 1], query[i, 2]))
# 処理時間計測START
tic()
# [step1] -50〜50の整数を上の式のxとyに代入して、「=」が成り立つ組合せをピックアップする
xy_candi = []
for x_i in range(-50, 50):
for y_i in range(-50, 50):
left_item = (x_i * query[0, 0]) + (y_i * query[0, 1])
right_item = query[0, 2]
if (left_item == right_item):
xy_candi.append(np.array([x_i, y_i]))
xy_candi = np.array(xy_candi)
print('--------------------------------')
print('[step1] -100〜100の整数を上の式のxとyに代入して、「=」が成り立つ組合せをピックアップする')
for i in range(len(xy_candi)):
print('(%2d * %2d) + (%2d * %2d) = %2d' %
(query[0, 0], xy_candi[i, 0], query[0, 1], xy_candi[i, 1], query[0, 2]))
# [step2] [step1]でピックアップしたxとyの組合せを下の式に代入して、「=」が成り立つ組合せをピックアップする
for xy_i in range(len(xy_candi)):
left_item = ((xy_candi[xy_i, 0] * query[1, 0]) +
(xy_candi[xy_i, 1] * query[1, 1]))
right_item = query[1, 2]
if (left_item != right_item):
xy_candi[xy_i, :] = -9999
xy_candi = xy_candi[(xy_candi[:, 0] != -9999), :]
print('--------------------------------')
print('[step2] [step1]でピックアップしたxとyの組合せを下の式に代入して、「=」が成り立つ組合せをピックアップする')
for i in range(len(xy_candi)):
print('(%2d * %2d) + (%2d * %2d) = %2d' %
(query[1, 0], xy_candi[i, 0], query[1, 1], xy_candi[i, 1], query[1, 2]))
print('x = %2d, y = %2d' % (xy_candi[i, 0], xy_candi[i, 1]))
# 処理時間計測END
print()
toc()
プログラムの出力結果は、以下となります。
--------------------------------
[step0] 問題を定義
4x + -3y = -9
3x + -7y = 17
--------------------------------
[step1] -100〜100の整数を上の式のxとyに代入して、「=」が成り立つ組合せをピックアップする
( 4 * -39) + (-3 * -49) = -9
( 4 * -36) + (-3 * -45) = -9
( 4 * -33) + (-3 * -41) = -9
( 4 * -30) + (-3 * -37) = -9
( 4 * -27) + (-3 * -33) = -9
( 4 * -24) + (-3 * -29) = -9
( 4 * -21) + (-3 * -25) = -9
( 4 * -18) + (-3 * -21) = -9
( 4 * -15) + (-3 * -17) = -9
( 4 * -12) + (-3 * -13) = -9
( 4 * -9) + (-3 * -9) = -9
( 4 * -6) + (-3 * -5) = -9
( 4 * -3) + (-3 * -1) = -9
( 4 * 0) + (-3 * 3) = -9
( 4 * 3) + (-3 * 7) = -9
( 4 * 6) + (-3 * 11) = -9
( 4 * 9) + (-3 * 15) = -9
( 4 * 12) + (-3 * 19) = -9
( 4 * 15) + (-3 * 23) = -9
( 4 * 18) + (-3 * 27) = -9
( 4 * 21) + (-3 * 31) = -9
( 4 * 24) + (-3 * 35) = -9
( 4 * 27) + (-3 * 39) = -9
( 4 * 30) + (-3 * 43) = -9
( 4 * 33) + (-3 * 47) = -9
--------------------------------
[step2] [step1]でピックアップしたxとyの組合せを下の式に代入して、「=」が成り立つ組合せをピックアップする
( 3 * -6) + (-7 * -5) = 17
x = -6, y = -5
elapsed time: 0.020077229 [sec]
こちらの解法でも、連立方程式が自動で解かれました。
こちらも1秒以内の時間で解かれましたので、人間よりも圧倒的に高速ですね。
このプログラムで実施していることは、xとyに「-50〜50」の全ての整数を代入してみては、方程式の「=」が成立するかどうかを確認する、という処理を繰返しています。
先程の伝えたように総当たり戦です。
この総当りのことを機械学習系の論文では、brute-forceと呼んだりします。
ちなみに、このbrute-force方針だと、変数が複数存在するようなケースでも解くことができます。
例えば、以下の問題です。

そして、この問題を解くためのプログラムが、少し難しくなりますが、以下となります。
# tic, toc refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# numpyを使います
import numpy as np
import itertools
# work
char_tmp = np.array(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'], dtype=np.object)
# [step0] 問題を定義
# refer from [https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1282759072]
query = np.array([[1, 1, 1, 1, 10],
[1, 2, 3, 6, 22],
[1, 3, 4, 5, 26],
[1, 4, 7, 7, 37]])
D = np.shape(query)[1] - 1
candi = np.array(list(itertools.product(np.arange(-20, 21), repeat=D)))
print('--------------------------------')
print('[step0] 問題を定義')
for query_i in range(len(query)):
for char_i in range(D):
print('%2d%s' % (query[query_i, char_i], char_tmp[char_i]), end='')
if (char_i != (D - 1)):
print(' + ', end='')
else:
print(' = ', end='')
print('%2d' % query[query_i, -1])
# 処理時間計測START
tic()
# [step1] -20〜20の整数を方程式の変数に代入して、「=」が成り立つ組合せをピックアップする
for candi_i in range(len(candi)):
for query_i in range(len(query)):
if (candi[candi_i, 0] != -9999):
left_item = np.dot(candi[candi_i, :], query[query_i, :-1])
right_item = query[query_i, -1]
if (left_item != right_item):
candi[candi_i, :] = -9999
break
candi = candi[(candi[:, 0] != -9999), :]
print('--------------------------------')
print('[step1] -20〜20の整数を上の式のxとyに代入して、「=」が成り立つ組合せをピックアップする')
for candi_i in range(len(candi)):
for query_i in range(len(query)):
for char_i in range(D):
print('(%2d * %2d)' % (query[query_i, char_i], candi[candi_i, char_i]), end='')
if (char_i != (D - 1)):
print(' + ', end='')
else:
print(' = ', end='')
print('%2d' % query[query_i, -1])
for char_i in range(D):
print('%s = %2d' % (char_tmp[char_i], candi[candi_i, char_i]), end='')
if (char_i != (D - 1)):
print(',', end='')
else:
print()
# 処理時間計測END
print()
toc()プログラムの出力結果は以下です。
--------------------------------
[step0] 問題を定義
1a + 1b + 1c + 1d = 10
1a + 2b + 3c + 6d = 22
1a + 3b + 4c + 5d = 26
1a + 4b + 7c + 7d = 37
--------------------------------
[step1] -20〜20の整数を上の式のxとyに代入して、「=」が成り立つ組合せをピックアップする
( 1 * 4) + ( 1 * 3) + ( 1 * 2) + ( 1 * 1) = 10
( 1 * 4) + ( 2 * 3) + ( 3 * 2) + ( 6 * 1) = 22
( 1 * 4) + ( 3 * 3) + ( 4 * 2) + ( 5 * 1) = 26
( 1 * 4) + ( 4 * 3) + ( 7 * 2) + ( 7 * 1) = 37
a = 4,b = 3,c = 2,d = 1
elapsed time: 10.909837961 [sec]
変数が4つの場合でも、解くことが出来ました。
これは、最初に紹介した加減法では、なかなか難しい問題です。
尚、同じ計算を、人間が電卓叩きながら実践した場合、どのくらいの時間がかかるでしょうか?
数時間はかかってしまいそうな気がしますね。
しかしながら、上記の結果については、コンピュータといえども、10秒の処理時間がかかっています。
問題が複雑になってきて、割と処理時間が膨らんできました。
また、上記プログラムの総当りは、a・b・c・dに、それぞれ「-20〜20」の全ての整数をセットするようにして探索を実施しています。
仮に、「-50〜50」や、「-100〜100」という風に探索範囲を広げていくことを考えると、処理時間はますます膨らんでいくことでしょう。
「-20〜20」という探索範囲内に、解が存在しなかった場合には、処理時間がかなり深刻になってきます。
この辺りが、コンピューターの計算速度の限界になります。
いくら早くても、限界はあるのです。
その為、上記プログラムのような、コンピューターに探索を丸投げするような方針では、厳しいのです。
ちなみに、プログラムをつぶさに見てもらうと、for文をbreakしたり、一度棄却された探索の候補を、2度目以降は参照しないようにする等、それなりの工夫はしています。
しかし、それでは足りない、抜本的な解決にはなっていない、ということです。
連立方程式解答例:(3)機械と人間の工夫のミックスで解く
次は、先程の10秒かかっていたプログラムを改良して、もっと高速に、もっと広範囲に、探索ができるかどうかを考えてみましょう。
それを実現するためには、機械の計算速度を更に上手く活かせるような、アルゴリズムの工夫を考えます。
今回課題に関するアルゴリズムの工夫は、頑張って考えれば実現できそうです。
というのも、先程の探索の仕方は、いくらなんでも冗長過ぎます。
「-20〜20」の整数を、a・b・c・dの4変数に対して、愚直に代入しているので、探索回数は「41 ✕ 41 ✕ 41 ✕ 41 = 2,825,761」となります。
凄まじい数ですね…。
逆に、10秒で終わっているのが素晴らしく思えてきます。
アルゴリズムの工夫については、この計算回数を如何に減らすかがポイントです。
探索回数が半分になれば、概ね計算時間も半分になります。
どうやったら、それが実現できるかを考えます。
王道なのは、当たりが悪そうな範囲の探索を棄却することです。
イメージ的には以下です。

割と、直感的な動作かと思います。
最初は、グリッドの粒度を荒く、広い範囲を探索し、当たりの良さそうなポイントを掘り下げる形で、探索ポイントを狭めていく。
そんなアルゴリズムです。
尚、当たりが良いか悪いかの判断については、アイデア勝負になりますが、例えば、左辺に代入した結果と、右辺の値との乖離度合いを評価すると良いかもしれません。
イメージとしては、以下です。

最終的に、4つの方程式全てについて、差分がZEROとなるa・b・c・dの組合せを探すことが、連立方程式を解くということのゴールとなりますが、1つの式で大きく乖離が出ていたり、他の4つの式でも大きく乖離が出ている場合、その周辺に解が無いことは想像できるかと思います。
人間が、連立方程式を解く場合、そういう想定は自然と行うかと思いますが、それを機械にも実践してもらう訳です。
それをプログラムで表現すると以下となります。
# tic, toc refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# numpyを使います
import numpy as np
import itertools
# work
char_tmp = np.array(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'], dtype=np.object)
# [step0] 問題を定義
# refer from [https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1282759072]
query = np.array([[1, 1, 1, 1, 10],
[1, 2, 3, 6, 22],
[1, 3, 4, 5, 26],
[1, 4, 7, 7, 37]])
# query = np.array([[1, 1, 1, 1, 2],
# [1, -1, 1, 2, 5],
# [3, 2, -1, 1, -3],
# [2, 1, 1, -3, -2]])
D = np.shape(query)[1] - 1
print('--------------------------------')
print('[step0] 問題を定義')
for query_i in range(len(query)):
for char_i in range(D):
print('%2d%s' % (query[query_i, char_i], char_tmp[char_i]), end='')
if (char_i != (D - 1)):
print(' + ', end='')
else:
print(' = ', end='')
print('%2d' % query[query_i, -1])
# 処理時間計測START
tic()
# 広範囲・間隔広めの整数を、最初の候補として定義
candi = np.array(list(itertools.product(np.arange(-100, 101, 20), repeat=D)))
# 答えが見つかるまでループ
while (True):
# コスト(左辺と右辺の差)を格納する変数を定義
cost = np.zeros([len(candi)])
# 候補の数字を与えられた方程式の変数に代入して、コスト(左辺と右辺の差)を計算
for candi_i in range(len(candi)):
for query_i in range(len(query)):
left_item = np.dot(candi[candi_i, :], query[query_i, :-1])
right_item = query[query_i, -1]
cost[candi_i] += np.abs(left_item - right_item)
# コスト(左辺と右辺の差)と、それが小さい候補の組合せをピックアップ
candi_best = candi[cost == np.min(cost)]
cost_best = cost[cost == np.min(cost)]
print('--------------------------------')
print('candi_best = ')
print(candi_best)
print('cost_best = ')
print(cost_best)
# コスト(左辺と右辺の差)がZEROである(解が見つかっている)かどうかを判定
if (np.min(cost_best) == 0):
# 解が見つかっている場合、それを表示
print('--------------------------------')
print('解に到達')
for candi_i in range(len(candi_best)):
for query_i in range(len(query)):
for char_i in range(D):
print('(%2d * %2d)' % (query[query_i, char_i], candi_best[candi_i, char_i]), end='')
if (char_i != (D - 1)):
print(' + ', end='')
else:
print(' = ', end='')
print('%2d' % query[query_i, -1])
for char_i in range(D):
print('%s = %2d' % (char_tmp[char_i], candi_best[candi_i, char_i]), end='')
if (char_i != (D - 1)):
print(',', end='')
else:
print()
break
else:
# 解に到達できなかったら、最もコストが低かった周辺の探索を、更に追加実施する
candi_range = 3
candi_adjust = np.array(list(itertools.product(np.arange(-candi_range, (candi_range+1)), repeat=D)))
# 解が複数存在すること
candi = np.zeros([0, D])
for candi_i in range(len(candi_best)):
candi_tmp = candi_adjust + candi_best[candi_i]
candi = np.concatenate([candi, candi_tmp], axis=0)
candi = np.unique(candi, axis=0)
# 処理時間計測END
print()
toc()プログラムの出力結果は、以下となります。
--------------------------------
[step0] 問題を定義
1a + 1b + 1c + 1d = 10
1a + 2b + 3c + 6d = 22
1a + 3b + 4c + 5d = 26
1a + 4b + 7c + 7d = 37
--------------------------------
candi_best =
[[20 0 0 0]]
cost_best =
[35.]
--------------------------------
candi_best =
[[17. 1. 3. -1.]]
cost_best =
[13.]
--------------------------------
candi_best =
[[14. -1. 5. -1.]
[17. -2. 5. -1.]]
cost_best =
[9. 9.]
--------------------------------
candi_best =
[[11. -2. 5. 0.]
[11. 1. 3. 0.]]
cost_best =
[6. 6.]
--------------------------------
candi_best =
[[ 8. -5. 6. 1.]
[ 8. 2. 3. 0.]]
cost_best =
[4. 4.]
--------------------------------
candi_best =
[[5. 1. 3. 1.]]
cost_best =
[1.]
--------------------------------
candi_best =
[[4. 3. 2. 1.]]
cost_best =
[0.]
--------------------------------
解に到達
( 1 * 4) + ( 1 * 3) + ( 1 * 2) + ( 1 * 1) = 10
( 1 * 4) + ( 2 * 3) + ( 3 * 2) + ( 6 * 1) = 22
( 1 * 4) + ( 3 * 3) + ( 4 * 2) + ( 5 * 1) = 26
( 1 * 4) + ( 4 * 3) + ( 7 * 2) + ( 7 * 1) = 37
a = 4,b = 3,c = 2,d = 1
elapsed time: 0.929239988 [sec]
最初は、「-100〜100」の範囲を、20飛ばし「-100, -80, -60, ..., 60, 80, 100」という感じで探索していき、最も当たりの良さそうなところを中心に、「±5」の範囲を探索する。
以降は、それを解に辿り着くまで繰返す。
そういう形で、解の探索を実現しています。
そうしたところ、何も考えずに探索すると、「-20〜20」の範囲で10秒かかっていたものが、「-100〜100」の範囲で1秒かからなくなりました。
我ながら、なかなかな進歩ですね。笑
これがアルゴリズムを工夫することの効果になります。
繰り返しになりますが、コンピューターに無限の計算速度が備わっていれば、アルゴリズムの工夫は不要となります。
いずれにせよ、一瞬で計算が終わるからです。
しかし、現状、パフォーマンスの課題は残る為、先程のようなアルゴリズムの工夫による解決が、随時必要となります。
また、1世代前のコンピューターについては、アルゴリズムを工夫しても、尚、計算に時間がかかったでしょうから、確かに、機械学習の実践は厳しかったろうなと実感します。
特に、連立方程式の解を求めるアルゴリズムは、かなり単純なものなので。
尚、いわゆる機械学習というのは、いわゆるこういったコンピューターの計算力を活かした問題解決のことを言います。
試行錯誤をして、最適解に辿り着くアプローチのことです。
あたかも、人間のように考えて、連立方程式の解を導出しているようでいて、実は愚直に探索をしているに過ぎなかったりします。
これは、冒頭に話した通りです。
プログラムを読んでみてもらえると、更に、その感覚が腑に落ちるかと思います。
しかし、単なる探索だけであると、技術分野として陳腐な気もしてしまいますし、実際に、限界も浅いです。
例えば、先程の例にて、アルゴリズムの工夫で10倍超の高速化が実現されましたが、仮に、あの連立方程式の解が少数だった場合には、どうでしょう。
上記のプログラムのままでは、解が少数であると探索を終えることができません。
解を見つけるためには、探索をする粒度が細かくする必要があります。
ただ、そうすると、探索回数を増えてしまう為、計算時間がまた肥大してしまいます。
或いは、探索を現実時間内に終えるために、更なる工夫が必要となります。
そんな探索の壁を、如何にスマートに突破していくか。
その鍵が、冒頭に話させてもらった数学や統計学や物理学です。
元々、物理現象をシミュレーションするために、古くから発展してきた学問が、機械学習における探索において、大変機能します。
この点は、先人の知恵に対して、大いにリスペクトを感じるポイントです。
ある種、AI・機械学習は、これまでの人類の叡智の集合点とも言えるかもしれません。
その点からも、第四次産業革命の核となる技術であることが納得できます。
という訳で、機械学習は単なる探索だけではなく、更に深い世界がその先にあります。
基本的な考えは探索ですが、その探索を如何に効率良く行うか、或いは、如何に精度高く実践するか、といったノウハウについては、古今東西、様々な先駆者が開拓した理論が存在するのです。
先程、私が行ったアルゴリズムの工夫についても、別途存在するアルゴリズムの応用だったりします。
つまり、知恵の拝借、先駆者のアルゴリズムの横展開、といった感じです。
そんな数学を用いた連立方程式の解き方は、次に紹介します。
連立方程式解法:(4)線形代数の考え方を用いて解く
それでは、最後に、線形代数の考え方を用いた連立方程式の解法を紹介します。
今まで、色々なアルゴリズムを見てもらったと思いますが、この方法は、それの何れとも一線を画す、メチャメチャ秀逸な解法です。
解法を紹介する前に、先ず線形代数について説明をしたいと思います。
皆さんは、線形代数をご存知でしょうか?
理系の大学に進学した方ならば、勉強をしているかもしれません。
高度な数学科目になります。
線形代数については、以下に記事を書いていますので、そちらも参考にして下さい。
さて、それでは、線形代数で連立方程式を解いてみようと思います。
先ず、考え方について説明します。
対象とする問題は、先程も使用した以下とします。

さて、この問題を、以下のような行列積で表現します。

この「Ab = c」に対して、線形代数的なトリックを用いるのですが、それは、両辺の前方に、Aの逆行列A⁻¹を掛けることをします。
そうすると、「b = A⁻¹c」という式が出来上がります。
計算過程は以下になります。
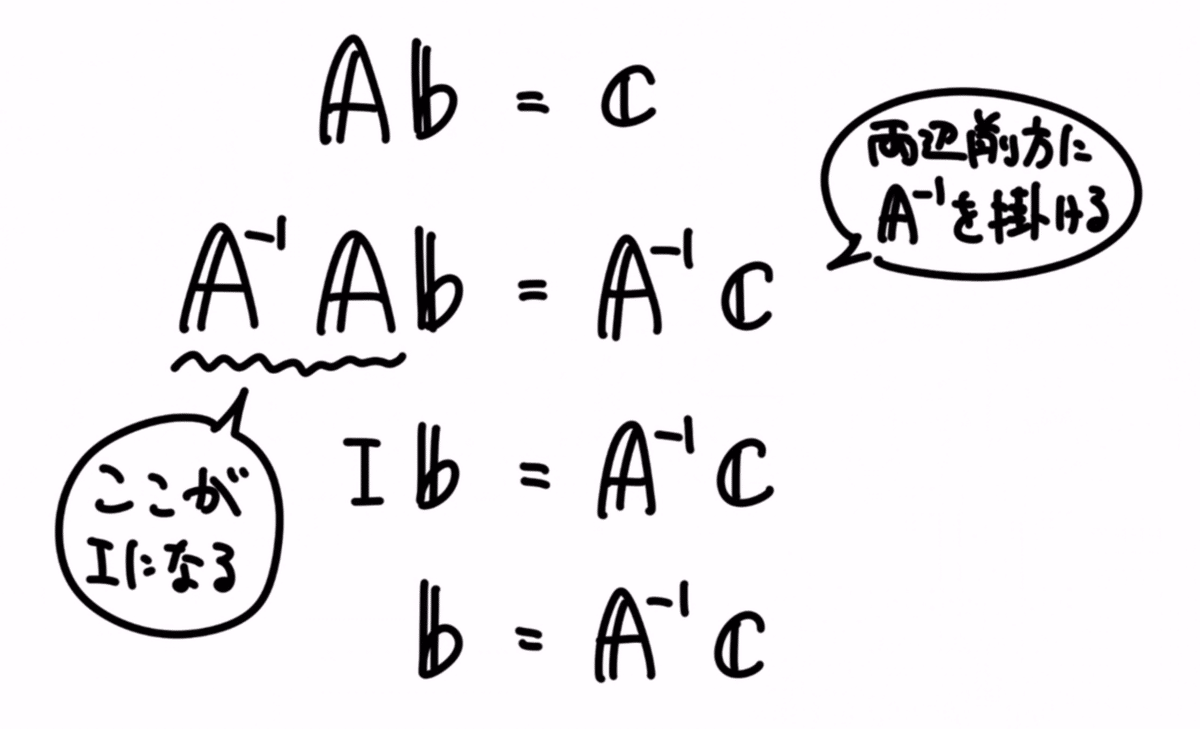
ここで、もし手で計算するとしたら、大変なのは逆行列を求める計算なのですが、幸い、逆行列を求める機能はnumpyに備わっているので、そこは一瞬で求まってしまいます。
即ち、連立方程式の解も、一瞬で求まってしまうのです。
以下に、プログラムを記載します。
# tic, toc refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# numpyを使います
import numpy as np
# [step0] 問題を定義
query = np.array([[4, -3, -9],
[3, -7, 17]])
# query = np.array([[4, 2, 2],
# [4, 5, -7]])
print('--------------------------------')
print('[step0] 問題を定義')
for i in range(2):
print('%2dx + %2dy = %2d' % (query[i, 0], query[i, 1], query[i, 2]))
# 処理時間計測START
tic()
# 連立方程式を解く
A = query[:, :2]
c = query[:, -1]
b = np.linalg.inv(A) @ c
print('--------------------------------')
print('x = %2d, y = %2d' % (b[0], b[1]))
# 処理時間計測END
print()
toc()プログラムの出力結果は、以下になります。
--------------------------------
[step0] 問題を定義
4x + -3y = -9
3x + -7y = 17
--------------------------------
x = -6, y = -5
elapsed time: 0.000245333 [sec]
一瞬で解けています。
素晴らしいアルゴリズムの秀逸さですね…。
素人の思い付きでは、最早、辿り着かない領域…。
これが、学問の境地です。
変数が4つのパターンも試してみましょう。
計算式は、全く同じで大丈夫です。
以下がプログラムです。
# tic, toc refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# numpyを使います
import numpy as np
# work
char_tmp = np.array(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'], dtype=np.object)
# [step0] 問題を定義
# refer from [https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1282759072]
query = np.array([[1, 1, 1, 1, 10],
[1, 2, 3, 6, 22],
[1, 3, 4, 5, 26],
[1, 4, 7, 7, 37]])
# query = np.array([[1, 1, 1, 1, 2],
# [1, -1, 1, 2, 5],
# [3, 2, -1, 1, -3],
# [2, 1, 1, -3, -2]])
D = np.shape(query)[1] - 1
print('--------------------------------')
print('問題を定義')
for query_i in range(len(query)):
for char_i in range(D):
print('%2d%s' % (query[query_i, char_i], char_tmp[char_i]), end='')
if (char_i != (D - 1)):
print(' + ', end='')
else:
print(' = ', end='')
print('%2d' % query[query_i, -1])
# 処理時間計測START
tic()
# 連立方程式を解く
A = query[:, :-1]
c = query[:, -1]
b = np.linalg.inv(A) @ c
print('--------------------------------')
for char_i in range(D):a
print('%s = %.1f' % (char_tmp[char_i], np.round(b[char_i])), end='')
if (char_i != (D - 1)):
print(', ', end='')
else:
print()
# 処理時間計測END
print()
toc()
プログラム出力結果は、以下となります。
--------------------------------
問題を定義
1a + 1b + 1c + 1d = 10
1a + 2b + 3c + 6d = 22
1a + 3b + 4c + 5d = 26
1a + 4b + 7c + 7d = 37
--------------------------------
a = 4.0, b = 3.0, c = 2.0, d = 1.0
elapsed time: 0.009639978 [sec]
変数4つでも一瞬です。
いや、本当に素晴らしいです…。
機械学習のアルゴリズムの中には、こういった学問的に秀逸なアルゴリズムを適用しているものが多々あります。
或いは、そういったものを知っているか否かで、アルゴリズムの構築精度が大きく変わってきます。
データサイエンティストや、機械学習エンジニアが、知識や経験を求められるのは、こういう側面からでしょう。
アルゴリズムを知っているか否かで、パフォーマンスが圧倒的に変わってくるのです。
或いは、自分を過信せず、常にリサーチを怠らないことの重要性が、ここにあるのかと思います。
その意味では、実務とリサーチを常に繰返していかなければならないのが、機械学習と付き合う上での宿命とも言えます。
なかなかタフな仕事、かつ、お勉強と仕事との線引が難しい仕事、と言えるかと思います。
おわりに
以上で、機械学習と連立方程式のクダリを終えます。
ここまで読んでくださった方、本当にありがとうございました。
サクッと書くつもりが、思わぬ大作となってしまいました…。
この記事が気に入ったらサポートをしてみませんか?

