Segment Treeについて

備忘録：Segment Treeが使えるようになる。

2020年12月16日：追記
Segment Treeの拡張、抽象化

先日のabc179で用いたsegment treeについてライブラリの整理だったり、自分の理解のためだったりと、様々な用途のためにまとめていきます。初学者の私でも理解できるように冗長に書いていくので興味がありましたら目をとめていただけると幸いです。

また、今回は最も基本的なSegment Treeである、区間の最小値取得（Range Minimam Query : RMQ）に絞って書いていきます。

そもそも何ができるのか

まずは、Segment Treeとはそもそも何なのかについてです。以前にフェニック木（Fenwick Tree ）やBITと呼ばれるデータ構造について書きましたが、それの派生形な感じです。というよりは、もとのSegment Treeを簡略化したものがBITらしいので、こちらのほうが基本に忠実で理解しやすいと思います。

Segment Treeとは、

区間における最小値を高速に取得する

データ構造です（RMQ以外では、最大値や区間和など様々な機能にすることができます）。どれくらい高速かというと、通常 n 要素の最小値を求める際には、n 回のアクセスが必要となりますが、本手法では log n回のアクセスで可能となります。

もちろん、区間における最小値を取る配列を用意しておけば1回のアクセスでできるじゃん、となりますが、そうすると更新の際に n 回のアクセスが必要となります。

更新と最小値取得がいい感じで実現できるのがSegment Treeです。

segment treeの構成要素

segment treeは完全２分木により構成されます。そして、機能として「値の更新」と「最小値の取得」を持ちます。

機能の説明をする前に、データ構造の説明をします。例として、通常の配列だと

v_normal = {5, 3, 6 ,1 ,7 ,8, 2, 4}

となるものを考えます。

Segment Treeは次図のような構造をしています。

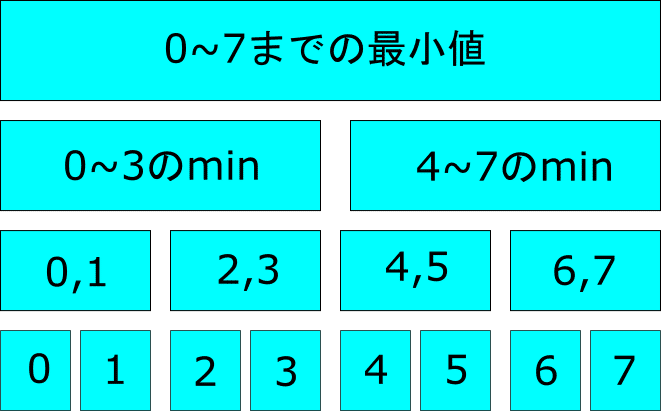
まず一番下の段に、通常の配列の要素を詰め込んでいきます。

次は一つ上の段に取り掛かります。下の2つの子どものうち、より小さい要素を書き込んでいきます。という作業を一番上の段まで行います。

赤字はインデックス番号です。結局のところsegment treeの配列は

v_seg = {1, 1, 2, 3, 1, 7, 2, 5, 3, 6, 1, 7, 8, 2, 4}

になります。7番目以降は通常の配列と同じになりますね。

今回は、要素数n=8で2の累乗であるため、seg木の要素数は2n-1となっています。もし、2の累乗じゃないときは、nより大きく最も近い2の累乗にします。
n =10なら16、55なら64といった感じです。余った個所には非常に大きい値を適当に詰めておきます。

これで、Segment Treeは完成です。次から、どうやって更新と最小値の取得をするかをプログラムを交えながら説明していきます。

更新

まずは、更新です。BITに比べれば非常に単純で分かりやすいと思います。

更新は一番下の子どもから順に行います。試しに通常配列の4番目、seg木配列の11番目の7を0に更新してみます。

まずは、11番目の７を1に書き換えます。次に11番目の親は5番目なので、5番目の2つの子どもを比べて小さいほうを5に書き込みます。今回は11番目は1、12番目は8なので、1に更新をします。

5の親は2です。そのため、子供である1と2を比べて小さい1に更新をします。

これを、一番上の親まで行います。

さて、11の親は5、5の親は2と当たり前のように行いましたが、図がないときにどうやるのでしょうか。これは、データ構造が2分木で構成されているため、

親番号 = (子番号 - 1) // 2

で求まります。小数点以下切り捨てです。

5 = (11 - 1) // 2 
2 = (5 - 1) // 2

よさそうですね。実装はこんな感じです。

 void update(int k, T x){
  k += n - 1;
  v[k] = x;
  while(k > 0){
    k = (k - 1) / 2;
    v[k] = min(v[k*2+1], v[k*2+2]);
  }
}

通常配列のインデックスをseg木配列に変換するため、n-1を足しています。最も上の親に達するまで、whileにて更新をかけています。

最小値取得

次に最小値を取得する機能について説明をします。最小値の取得は親から子ども下っていき、区間に収まるまで探索をしていきます。

今回は先にプログラムを示して、それに従って説明をします。

 T query(int a, int b) {return query_sub(a,b,0,0,n);}
T query_sub(int a, int b, int k, int l, int r){
  if(b <= l || r <= a) return inf;
  if(a <= l && r <= b) return v[k];
  T c1 = query_sub(a, b, 2*k+1, l, (l + r) / 2);
  T c2 = query_sub(a, b, 2*k+2, (l + r) / 2, r);
  return min(c1, c2);
}  

まず、変数について説明します。

a : 最小値を求める区間の最小値
b : 最小値を求める区間の最大値+1(開区間実装)
k : ノードのインデックス（seg木のインデックス）
l : 探索している区間の左端
r : 探索している区間の右端+1（開区間実装）

です。このうち、kのみseg木のインデックスで、a, b, l, r は通常配列のインデックスです。

最小値の取得では、親から子に下っていき l と r を変化させていきます。それが、a, bの区間にすっぽりと入っているところの値を取得していきます。そのうち、値が最も小さいものを返します。

もうちょっと詳しく見ていきます。

a = 3, b = 7の 3~6の中の最小値を取得してみます。まずは、queryから、query_subを呼びます。query_subでは変数として、k = 0, l = 0, r = nなので、seg木インデックス0で、0~n-1までの全区間ということで、seg木の一番上からスタートします。

当然ですが、0~n-1は3~6にはすっぽりとは収まりません。そのため、右方向と左方向の子どもに分かれて探索を続行します。これは、最後のelse文のところです。値が2つありますが、それぞれの子どもにあたります。

ここで、親から子のアクセスについて補足します。

親から子には

左子番号  =  親番号 * 2 + 1
右子番号  =  親番号 * 2 + 2

でアクセス可能です。

上の値、左側の子どもに行きましょう。まず、引数は

query_sub(a, b, k * 2 +1, l, (l+r) / 2 )

となっています。a, b は固定で、kは左子番号、左に行ったので左区間は l で変化なし、右区間 r は区間端の平均を取ることで半分にしています。

実際の値はquery_sub(3, 7, 1, 0, 4)となります。0~3となりましたが、まだ3~6に入っていません。そのため、また子どもに行きます。右に行きます。

query_sub(3, 7, 4, 2, 4)です。2~3です。もうちょっとですね。さらに右に行きましょう。query_sub(3, 7, 10, 3, 3)は3です。3~6にようやくすっぽりと収まりました。else if の v[k]を親に返してあげましょう。

今回は右に行ったり左に行ったりしましたが、プログラムでは両方に進行して、どんどん子どもを下っていきます。

というようにやっていくと、区間に入ったものはその値を返して、出てしまったものはinfを返すので、より小さい値が上の親にどんどん渡っていきます。

赤：一つ目のif文で return inf
緑：else ifでreturn v[i]
黄色：elseで子どもへの探索をした箇所

一番上の親まで返った値が、無事その区間の最小値となります。お疲れさまでした。

プログラム

長々と説明をしてきましたが実装になります。c++の構造体を用いています。

template<typename T>
struct segtree{
const T inf = numeric_limits<T>::max();
int n;
vector<T> v;
segtree(int n_){ //引数のnだからn_,struct内のnと区別する。
  int x = 1;
  while(n_ > x) x *= 2; 
  n = x;
  v.resize(2*n-1 ,inf);
}
void update(int k, T x){
  k += n - 1;
  v[k] = x;
  while(k > 0){
    k = (k - 1) / 2;
    v[k] = min(v[k*2+1], v[k*2+2]);
  }
}
T query(int a, int b) {return query_sub(a,b,0,0,n);}
T query_sub(int a, int b, int k, int l, int r){
  if(b <= l || r <= a) return inf;
  if(a <= l && r <= b) return v[k];
  T c1 = query_sub(a, b, 2*k+1, l, (l + r) / 2);
  T c2 = query_sub(a, b, 2*k+2, (l + r) / 2, r);
  return min(c1, c2);
}  
};

コンストラクタでnを2の累乗に変換し、配列を生成しています。あとは、説明した通りです。前回のabc179の解答で使用しているため、よろしければそちらもご覧ください。

非常に長くなりましたが記事は以上となります。解説部分を読み飛ばしても、プログラムをコピペすれば使用できるのでお急ぎの方は使ってみてください。

今後もアルゴリズムや構造に関するまとめを書いていきます。誰かのお役に立てれば幸いです。

追記：Segment Treeの抽象化

abc185にてSegment Treeにxor演算を載せる問題が出題されました。

F - Range Xor Query

この問題を解くために色々と勉強したので書いていきます。

まずsegment treeの使用条件です。

知らずに使っていたのですが、どうやら「モノイドである」ということが重要らしいです。モノイドの性質は次の通り。

・結合率を満たす
各元a,b,cに対して (a・b)・c = a・(b・c)を満たす。

・単位元を持つ
任意の元に対して (a・e) = (e・a) = aとなる e が存在する。

です。仰々しく書きましたが、考えてみればそんなに難しいことではありませんでした。上記の最小値を取る場合と対応させて考えましょう。

まず、結合率です。

例えば、インデックス0~5までの最小値を取るときを考えましょう。このときって、m1 = min(v[0],v[1])をやって、そいつと比べる（min(m1,v[2])）と頭から比べてるわけではないですよね。ある程度の区間の結果を保持しておいて、それらを使って効率的に最小値を求めています。

ということで、順番が入れ替わっても答えに影響がありません。だから、segment treeで扱えます。

逆に言うと、segment treeで処理するなら、結合率がないと答えがおかしくなっちゃうよ。ということです。

次に単位元です。

これは、最小値の場合のinfに対応します。では、なんでinfを用いたのでしょうか？

segment treeの構造は必ず、各段が2^n乗になっています。そのため、入力が2^nとなっていない場合には、余分な数字で空いている場所を埋める必要があります。しかし、好きな数字を使っても良いわけではありません。

正整数値の最小値を求める際に、空き配列を0で埋めたらどうなるでしょう。どんな場合においても0が出力されてしまいます。これはまずいです。

そのため、最小値ではinfという数字を空き配列に詰め込みました。そして、このときのinfが単位元となるわけです。

単位元で言われている

(a・e) = (e・a) = a

は演算結果が変わらないということなのですが、要するに、結果を邪魔しない数が存在しますよということです。そしてその数で埋めましょう。

これで、モノイドの説明はおしまいです。

「モノイドを理解して何になるのか」と考える方もいると思います。ただ、これを理解できると1つ嬉しいことがあります。もしかしたらいっぱいあるかもしれません。

それは、最小化用に作成したsegment treeをとっても簡単に別の演算を書き換えることができるようになることです。

segment treeで大切なのは、結合率を満たす演算とその演算における単位元です。モノイドですね。

ということで、その部分を引数として持つことにより、外部から指定できるように書き換えてあげましょう。

//0-indexed
template<class T, T (*op)(T,T), T(*e)()>
class segtree
{
private:
   int n;
   vector<T> v;
public:
   segtree(int n_)
   {
       int x = 1;
       while (n_ > x) x <<= 1;
       n = x;
       v.resize(2 * n - 1, e());
   }
      void set(int k, T x)
   {
       k += n - 1;
       v[k] = x;
       while (k > 0)
       {
           k = (k - 1) / 2;
           v[k] = op(v[k*2+1],v[k*2+2]);
       }
   }
   T get(int k) { return v[k + n - 1]; }
   //[a,b)
   T query(int a, int b) { return query_sub(a, b, 0, 0, n); }
   T query_sub(int a, int b, int k, int l, int r) {
       if (b <= l || r <= a) return e();
       if (a <= l && r <= b) return v[k];
       T c1 = query_sub(a, b, 2 * k + 1, l, (l + r) / 2);
       T c2 = query_sub(a, b, 2 * k + 2, (l + r) / 2, r);
       return op(c1,c2);
   }
   
   //display segtree value
   void display(string text = "segtree value")
   {
       cout << text << endl;
       int cnt = 0;
       int end = 1 << cnt;
       int l = v.size();
       for (int i = 0; i < l; ++i)
       {
           cout << v[i] << " ";
           if (i == end - 1) 
           {
               ++cnt;
               end += 1<<cnt;
               cout << endl;
           }
       }
       cout << endl;
   }
};

書き換えたものがこちらになります。内部の状態を見たかったので「display()」という関数を書いていますが、ただ見るだけの関数です。

0インデックス、クエリは半開区間で作ってあります。

最小値から変えたところは、

構造体からクラスにした（本質じゃない）
演算をop(T,T)で与えられるようにした。
単位元をe()で与えられるようにした。

です。先に述べたabc185Fはこちらのライブラリを使って解いていますので、使用法などはそちらをご覧いただけるとわかりやすいと思います。