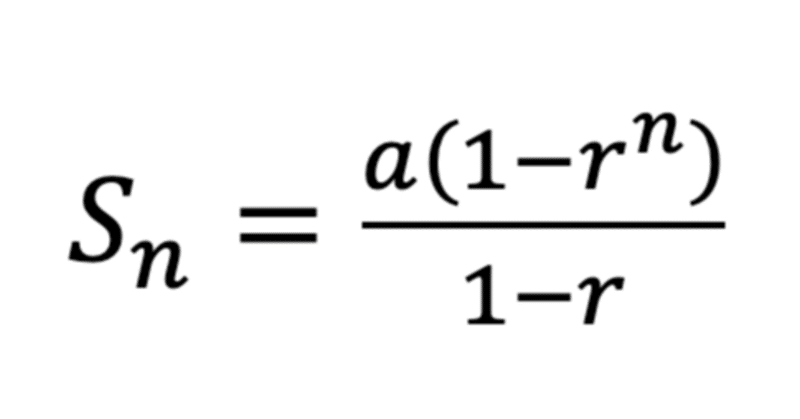
中小企業診断士で使う等比数列の和の公式について
こんばんは。 令和5年度中小企業診断士2次試験筆記に不合格となり、次の試験に向けて動き始めました。 応援してくださった皆さまに合格の報告が出来なかったことを心苦しく思うとともに、
次は絶対勝つために僕は勉強だけは最後までやっておく
ことを決意新たにしております。
今回の内容は、高校数学で習う等比数列の和の公式です。
もちろん、結果だけを公式として覚えても良いのですが暗記が大の苦手な私は大学受験の際に公式丸暗記だと、記憶違いを起こした時に死亡すると思い、導出方法をしっかりと理解することで、忘れてもその場で公式を導き出せるようにしました。 加減乗除の計算と指数、基本的な文字式の計算ができれば、等比数列の和の公式はそれほど難しくないと思っております。(個人の感想です)
記憶に残っている出来事として、高校時代私の隣の席のクラスメイトから質問されました。
質問された内容は単純な等比数列の和の問題で、彼は公式を覚えていなかったようでしたので公式を使えば一発で解けることを教え、その後で公式の導出方法を説明しようとしたのですが「いや、それは要らない」と言われました。
ゴリ押しはしませんでしたが、それを知っていれば色々と理解が深まるのになあと、他人事ながら残念に思った記憶があります。
(理系クラスでしたので、その思いが強かったのもあるのかもしれません)
この記事では、等比数列とはなにか? 等比数列の和の公式とは? 診断し試験でどこに等比数列が出てくるの? (記事が長くなったので次回)と言った内容を書いていきたいと思います。 ただし、数式の部分はnoteでは表せないのでWordで書いて画像としてアップロードしますのでご容赦ください。
かなり基本的な内容から書きますので、必要な部分だけつまみ食いしてお読みいただければと思います。
等比数列についての説明
そもそも等比数列とは?
数列(すうれつ)とは、ある一定の規則に従って順に並べられた数の列のことです。
例えば、 2,4,6、8、10、・・・のような偶数の集まりも、nを整数とすると n番目の数は n の2倍であると言うことができるため数列と言えます。
では、等比数列とは何か?といえば、 ある数と、その次の数の「比」が「等」しい数列のことを言います。
例えば、 2→4→8→16 は、前の数から次の数に進むには常に2という数をかけ算することになります。
この、次に進む際に掛け算する数のことを「公比」と言いますので覚えておいてください。
2と4を比で表すと 1:2。 4と8を比で表すと 1:2。
8と16を比で表すと 1:2
このように、隣り合う数の「比」が 1:2 と
「等」しいので等比数列と言います。
今回は簡単に公比が2の場合を表しましたが、公比を10とすれば
10→100→1000→10000になったり、
0.1にすると 0.1→0.01→.0.001 のように、小数で表すことも可能です。
また、数列の用語として先頭の数のことを「初項」と言います。
例えば、初項を3、公比を2とするとこの数列は
3→6→12→24→・・・ と表すことが出来ます。
初項と公比は後の説明で登場するので押さえておいてください。
100番目は?1億番目は?
先ほどの例では、最初から3つや4つ程度の少ない例で表しましたが、
じゃあ100番目の数はどうなるの? 1億番目は?
というと、計算が大変になります。 また、1番目は◯、2番めは◯などと
1つずつ全部を書いていくと永久に終わりません。
そこで、中学で習う文字式と、指数というものを使います。
指数は、3の4乗 のように 同じものを何回もかけ算するものを表します。 そして、数列では n番目の数は何?というものを、nを使って計算できる形で表します。
例えば、n番目の数が n+3 と表せれば、100番目の数は nを100に置き換えて計算し、 100+3=103 と計算できるし、1億番目と言われれば
1億+3を計算すれば求めることが出来ます。
このように、n番目の数をnを使って表すことを一般化といいます。
(一般化という言葉は覚えなくても大丈夫です。それより、先ほどの初項と公比をしっかりと覚えてください)
また、特に数列において n番目の数を nを使って表したものを 一般項と言います。
では、等比数列の一般項とは?
等比数列は何だったかというと、前の数に公比をどんどんかけ算していくものでした。 しかし、最初の数は前がありませんので、ここについては初項を使います。
例えば、初項が3,公比が2の数列は
1番目は初項の 3
2番めは 1つ前の3に公比の2をかけて6
3番めは 1つ前の6に公比の2をかけて12
4番めは 1つ前の12に公比の2をかけて24
このように表すことが出来ます。 しかし、このままでは100番目を求めるためには最初から100回計算しなければなりません。
ですが、文字nをつかってn番目の数を表すことができれば、100番目でも1億番目でも一度に求めることが出来ます。(計算自体はとても面倒ですが・・・)
では、等比数列のn番目を文字を使って表すにはどうすればよいのか?
先ほどの例をもう少し分解してみてみましょう
1番目は初項の 3
ここは変わりません。
2番めは 1つ前の3に公比の2をかけて6
これを式に表すと
3✕2
3番めは 1つ前の6に公比の2をかけて12
ということで、6✕2 と計算できるのですが
この6という数は 2番めで計算した 3✕2でした。つまり3番めは
3✕2✕2 と表すことが出来ます。
では、4番目は?
4番めは 1つ前の12に公比の2をかけて24
この12という数は3番めの計算結果なので
3✕2✕2✕2
と表すことが出来ます。
ここまでのルールをまとめてみると
[1番目] 3
[2番目] 3✕2
[3番目] 3✕2✕2
[4番目] 3✕2✕2✕2
なにかに気づきませんか? そう、
3に対して、1つ進むごとに2をかける回数が1つずつ増えています
ただし、3番めのときは2回のように
n番目のときは、nより1つ少ない n-1回だけ 2をかけ算しています。
つまり、n番目の数は 3✕(2をn-1回掛け算) と表すことが出来ます。ただし、 2をn-1回かけ算というののは 2のn-1 乗 と表しましょう。
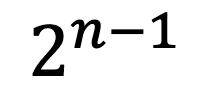
ということで、初項3 公比2の等比数列の一般項(n番目の数)をAnとすると次のように表すことが出来ます。
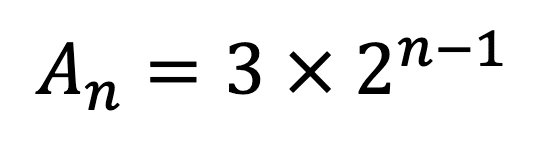
初項・公比も文字にしてしまおう
前の説明では、初項を3、公比を2としましたが、他にも等比数列はあります。 そこで、私の時代の高校数学では 初項をa 公比を r としていたのでここから先はそのように文字を使いたいと思います。
An = 3✕2^(n-1) この、先ほど導き出した式について、初項を3からaに、
公比を2からrに変換することで、初項a,公比rの等比数列は
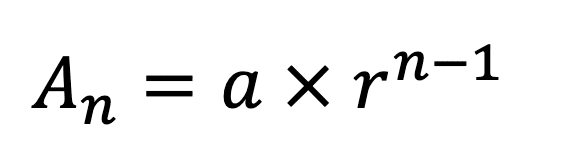
と表すことが出来ます。 (説明用に✕をあえて書いています。)
本題の等比数列の和の公式
まずは簡単な例から
せっかく文字式として一般項を表したのですがイメージを掴むため
また初項3、公比2の数列に戻りましょう。
その数列を実際に5番目まで書いてみると
3,6、12,24,48 となります。
この5つの数を足すことで、この等比数列の1から5番目までの和を
求めることが出来ます。
これらを実際に足し算すると、93となり求めることが出来ました。
100番目まで足したら?1億番目は?
このタイトルを見るだけでもイヤになりますよね。
とりあえず、等比数列の一般項の表し方は先ほど説明したとおりなので
100番目の数は 3✕2の99乗 ということはわかりますが、
1から100番目まで足し算すると
3+6+12+24+48+・・・+ 3✕2の99乗
1億番目まで足し算すると、 +を99999999個書かなくてはなりません。
もう少しスッキリさせたい。(注 この記事でも実際の数までの計算はできませんが、スッキリと表すことまでを目標にします。)
+を 99999999回も書かずに表す方法をご説明します。
等比数列の和の公式は計算の工夫の結果
例えば、30人のクラスで1人千円づつを集めたときの合計で
1000+1000+1000+・・・ と1000を30回も足し算する人は居ないと思います(居たらごめんなさい)
この同じものを足し算するという無駄をなくすために我々はかけ算をという工夫をします。(今では当たり前ですが、初めてかけ算を発明したときは世紀の大発見だったのではないかと思っています。)
等比数列の和の公式では、1から1億番目までを足し算する場合、1億個の同じではない数を足し算することになるため、かけ算を使うことが出来ません(公比が1のような一部例外はありますがそれは今回は説明しません)
しかし、足し算部分をほぼすべてゼロにすることができれば?
計算は圧倒的になりますよね
例えば、最初と最後はゼロではないけど、途中が全部ゼロだとすれば
100個であろうが、1億個であろうが全く怖くないわけです。
最初が3、最後が5,途中が全てゼロであれば、1億個の数があったとしても
3+0+0+(途中が全部ゼロ)+0+5
のように、最初と最後だけを計算すれば合計を求めることができます。
そして、等比数列の和は、ある方法によって途中の足し算をすべてゼロにすることができます。(厳密には最後に割り算が必要になりますが、1億回足し算するよりマシです)
公比をかけて引き算する
どうやるかをネタバラシになりますが、公比rをかけ算したものを
もとの和の式から引き算すると、ほとんどの足し算部分がゼロになって消えてくれます。
実際に文字式で等比数列の和を表すと下のとおりとなります。
(n番目までの数列の和はSnで表します)
等比数列のN番目はrの(n-1)乗だったので間違えないでください
なお、1番目からn番目までの和を Snと表します。
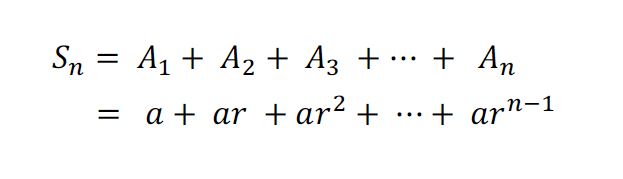
ここで、下側のSnの式の両辺に 公比 r をかけ算して並べてみます。
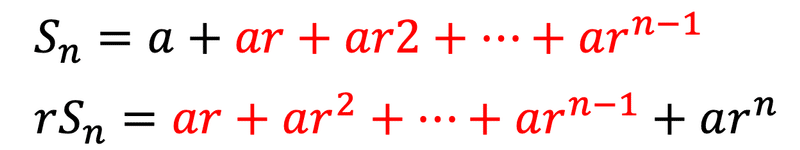
このように、赤い部分が全く同じ形になります。
同じものを引き算すれば、それはゼロになる(今回の一番のポイント)。
そこで、上の式から下の式を引き算すると
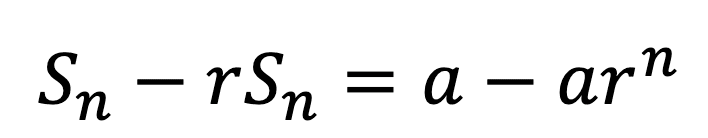
このようにかなりスッキリしました。 ただし、求めたいものは
数列の和である Sn であるので、この式を Sn = ? という式変形をします。
左辺を Sn で、 右辺を a でまとめると
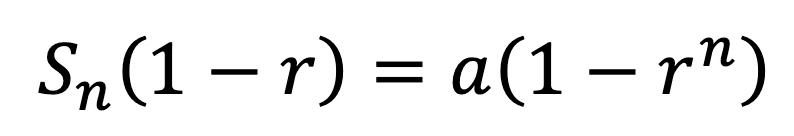
両辺を 1-r で割り算すると
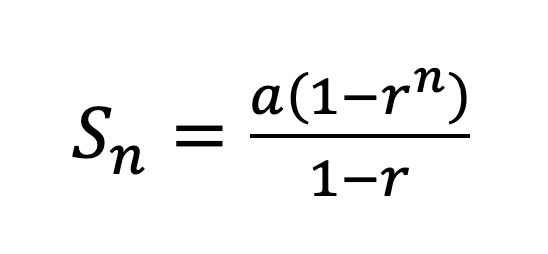
と、非常にスッキリした形で等比数列の和の公式を求めることが出来ました。 途中の足し算をうまく0にしてスッキリさせた計算の工夫の結果がこの公式になります。
実際にこの式が正しいかを確認してみましょう。
1億はとても計算が大変なので、 初項(a)3、公比(r)2の数列の5番目までの和を今作った式を用いて求めると、2の5乗は32なので
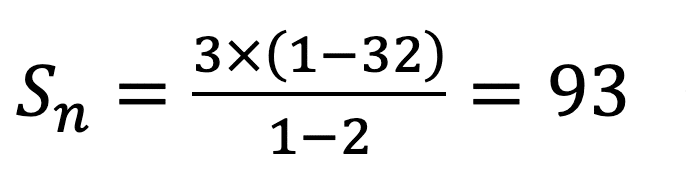
ということで、すべて足し算した場合と同じ結果を得ることが出来ました。
(参考) 3+6+12+24+48
この記事が気に入ったらサポートをしてみませんか?
