
線形代数をBlenderで、やる
「線形代数をBlenderで、やる」とはどういうことでしょう?
とりあえずこの画像を見てください
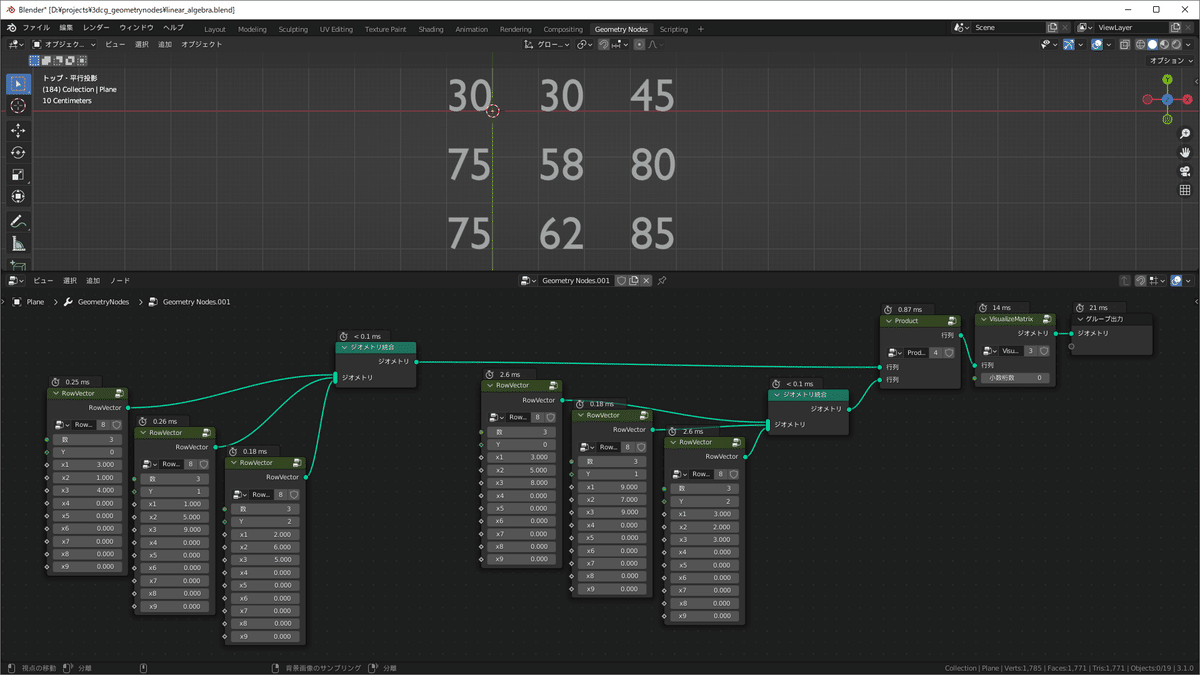
これだけではよくわからないと思いますが、
要するに下の画像と全く同じ計算をやっています

Blenderのノードの側にもよく見ると、3,1,4…と、
WolframAlphaの画像と同じ値が並んでいるのが確認できます

さて、このBlenderのノードシステム(GeometryNodes)ですが、
本来は3DCGのジオメトリをプロシージャルに生成にするためのもので、
決して線形代数をするための機能ではありません!
しかし、それをうまく悪用すれば使えば、
上のような行列の演算をさせて線形代数遊びができます!
この記事の最後では、これを応用して次のGIFのような
最小二乗法による楕円当てはめの計算が組み立てられるようになります

前提
この記事ではBlender3.1.0以降を用いて、
GeometryNodesにある程度慣れていることを前提に進めます
Blender3.1で新しく追加されたノードを多用することになるので、
必ず3.1以降のバージョンを用いてください
基本的な考え方とルール決め
まず、BlenderのGeometryNodesにはfloatやベクトル(3次元)といった型が扱える一方で、残念ながら行列の型は存在しません…!
ではどうするのかというと、代わりにジオメトリ(Geometry)を用います
具体的にはジオメトリの各頂点を行列の各要素とみなし、
その位置座標(X, Y, Z)を、(列番号, 行番号, 値)と定義することにします
便宜上、列番号と行番号は1-indexed(1, 2, 3, …, N)ではなく、
0-indexed(0, 1, 2, …, N-1)を用いることに注意してください
例えば、
$$
\begin{pmatrix}
3 & 1 & 4 \\
1 & 5 & 9 \\
2 & 6 & 5 \\
\end{pmatrix}
$$
という行列を表すジオメトリは次のようになります

また利便性のため、基本的には上の画像のように、
$$
頂点のインデックス = ( 列番号 \times 列数 + 行番号)
$$
が成り立つように頂点を並べることにします
(後述の列ベクトルのように、一時的にこれが成り立たなくなるケースは許すものとします)
また、列ベクトルは幅が1の行列、行ベクトルは高さが1の行列とみなすことにします
また、今回行列の幅と高さは最大でも9を上限とするように作ることにします
(9である意味は特にないので、各々必要な上限に読み替えても大丈夫です。ただし、楕円当てはめを行うためには少なくとも6次の正方行列が扱える必要があります)
零行列を生成する
手始めに幅と高さを指定してその大きさの零行列ジオメトリを生成するグループを作ってみます
これは次のようになります


そんなに複雑なグループではないので、見た通りかと思います
W×H個の頂点を生成するには「グリッド」ノードが便利ですが、
余計な辺と面も一緒に作られてしまうので「ジオメトリ削除」ノードで消しています
例えば、Wに4、Hに3をいれて出力すると、
ルール通りの4列3行の零行列を表すジオメトリが生成されるのがわかります

行列を可視化する
意図したジオメトリが生成されているかを確認するにはスプレッドシートも便利ですが、縦一列に並んでいるため少しイメージしづらいです
そのため、早めに行列を可視化するグループを作っておきましょう





81個のノードを並べてジオメトリを統合する手段も取れますが流石に大変すぎるので、ここでは「最大9次の行ベクトルを表示するグループ」を作って9個並べることにより、この手間をなるべく抑えています
「VisualizeValue」で各値を可視化するジオメトリを作成し、
「VisualizeRow」でそれらをまとめて行ベクトルにして、
「VisualizeMatrix」でさらにそれらをまとめて行列の可視化を行う、
という流れになっています
「PickWH」「PickValue_Index」というグループも作成しています
PickWHは「属性統計」ノードを使ってXY座標の最大値から行列の幅と高さを取り出します
PickValue_Indexも同じく「属性統計」ノードを使って指定したインデックスの値を取り出します
(補足 : ちなみに属性統計ノードがフィールドではなく単一の実数値を出力してくれるのがポイントです)

ベクトルと行列を生成する
値が0だけだとつまらないので、好きな値を設定できるようにしましょう

零行列のもとになる頂点の生成に「グリッド」ノードを利用したように、
RowVectorでは「メッシュライン」ノードを利用し、同じく辺を削除しています
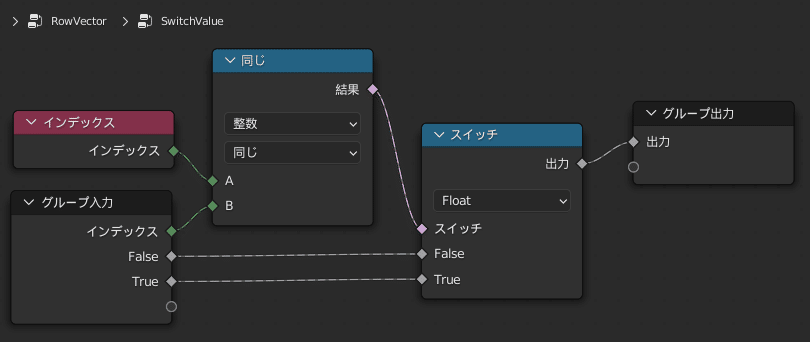
頂点のインデックスに従って値を設定したいので、
9連のSwitchValueグループを用いてそれを実現しています
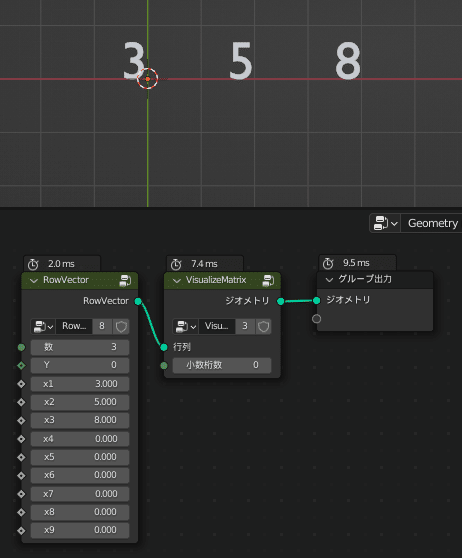
また、利便性のためにY座標をずらせるようになっているため、
適切に設定すれば冒頭の例のように「ジオメトリ統合」ノードで行列も簡単に生成できるようになります
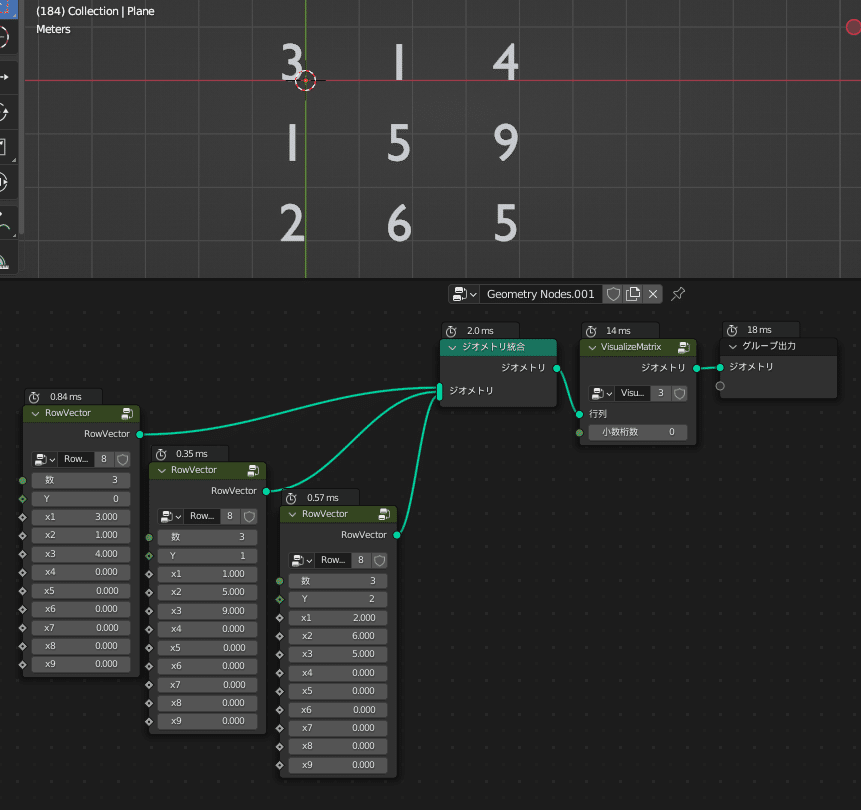
また、RowVectorと同じようにして、列ベクトルを生成するColumnVectorを作ることもできます
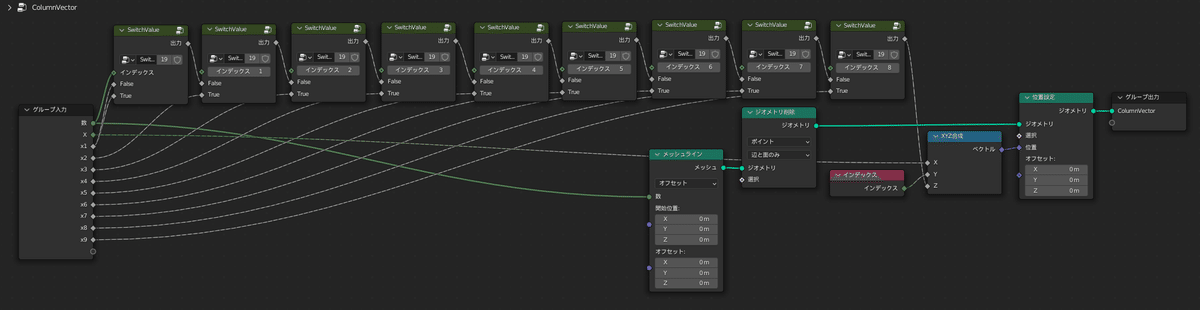

積を計算する
行列の積が計算できればできることがぐんと増えるので、次は積を作ってみます



上記のようにノードを結べば動くのですが、若干特殊なことをやっているので説明します
行列の積は、行列 $${A, B}$$ の積を $${C}$$ として、それらの要素をそれぞれ $${a_{xy}, b_{xy}, c_{xy}}$$ のように書くとすると、
$$
c_{xy} = \sum_{k=0}^{n-1} a_{ky}b_{xk}
$$
と表すことができます。
このとき、$${n}$$ は $${A}$$ の幅もしくは $${B}$$ の高さで、それらが一致しない場合は積が定義できません
今回の場合、$${n}$$ は多くても9個です。あえて $${\sum}$$ 記号を使わずに書くと、
$$
c_{xy} = a_{0y}b_{x0} + a_{1y}b_{x1} + a_{2y}b_{x2} + a_{3y}b_{x3} + a_{4y}b_{x4} + a_{5y}b_{x5} + a_{6y}b_{x6} + a_{7y}b_{x7} + a_{8y}b_{x8}
$$
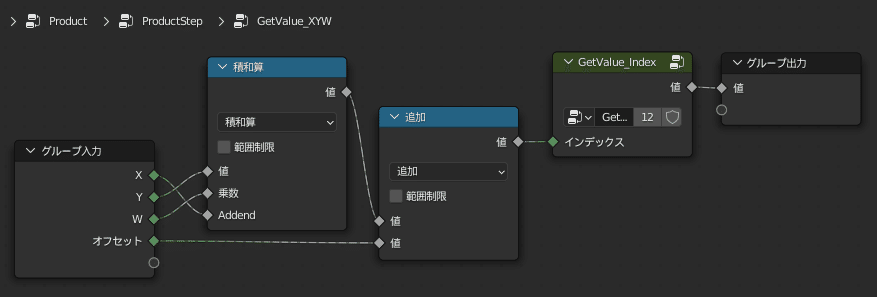
ということになり、この和を取る部分が「Product」グループにある9連「ProductStep」に対応します

また、もう一つの特筆すべきポイントは「ジオメトリ統合」ノードの使い方です

行列 $${C}$$ の値を計算するにあたって、行列 $${A}$$ のジオメトリと行列 $${B}$$ のジオメトリの頂点に同時にアクセスしたいので、ジオメトリは統合しておく必要があります
行列 $${C}$$ のための頂点は行列 $${A}$$ と行列 $${B}$$ の頂点をそのまま再利用することにしています
正方行列同士の積の場合などは $${A, B}$$ の要素数の和よりも積 $${C}$$ の要素数の方が多くなりますが、
例えば $${A}$$ が6次の列ベクトル、$${B}$$ が6次の行ベクトルの場合、その積 $${C}$$ の要素数は $${36}$$ 個になるため、そのままだと要素数が $${24}$$ 個足りません
足りていない場合のために頂点を補填する操作をしているのが次の画像の箇所です

「スイッチ」ノードを挟んでいます
Productを実際に使用してみた例がこちらです

WolframAlphaでも結果が一致していることがわかります

固有値を求める
さて、いよいよ線形代数っぽいことをやっていきます
はじめに述べた通り、楕円当てはめを最小二乗法で解けるようにしたいです
そのためには行列の最小固有値に対応した固有ベクトルが求められる必要があります
今回は次のようなアルゴリズムで固有値を求めることにします
Householder変換を用いて三重対角化(扱いやすいよう相似変換)
Householder行列を用いたQR法で最小固有値のだいたいの値を求める
Wilkinsonの移動法で原点移動をしつつQR法を行うことで収束を加速する
(厳密には1のステップは実対称行列の場合は三重対角行列、一般の行列の場合は上Hessenberg行列になります。楕円当てはめアルゴリズムでは実対称行列の固有値を求めることになるのでこの記事では対象が実対称行列であることを前提とし「三重対角化」と呼ぶことにします)
三重対角化
QR法では処理を反復することにより固有値を求めますが、反復1回あたりの処理コストはなるべく抑えたいです
そのため、QR法を行う前に相似変換を行い三重対角化をしておくのが一般的です(相似変換は固有値を変化させません)
こうすることで、QR法の反復1回にかかるコストを劇的に抑えることができます
相似変換の仕方にはいくつか選択肢がありますが、安定性に優れている「Householder変換」を用いるのが主流とされているようです
Householder変換を用いた三重対角化のアルゴリズムは英語版Wikipediaに例付きでわかりやすく載っていました
ではノードを組んでいきます

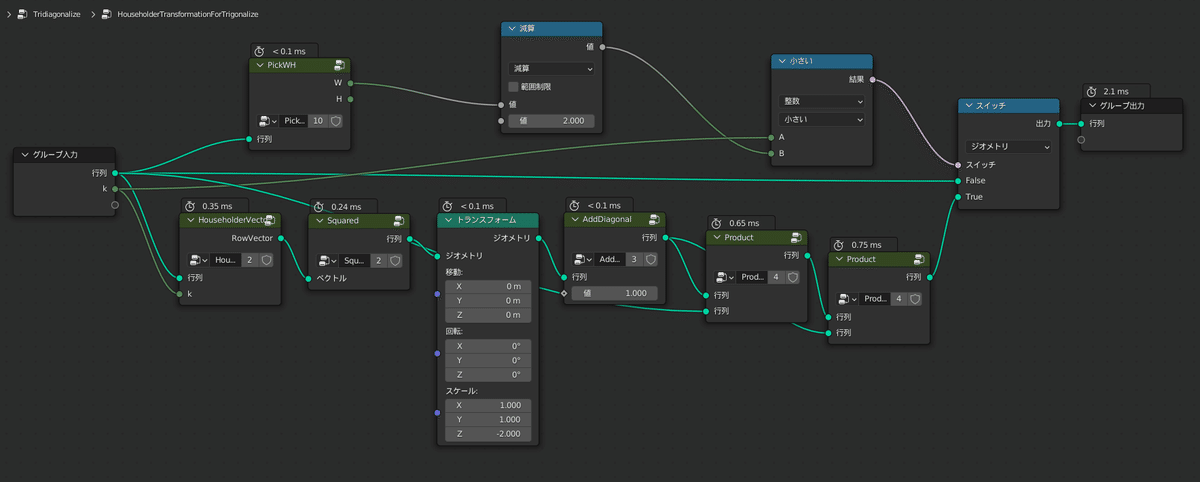




まず、n次の正方行列に対してHouseholder変換はn-2回行えば三重対角化ができるため、Householder変換のグループ「HouseholderTransfomationForTrigonalize」は7個繋げて最大7回行われるようにしています
「HouseholderVector」グループでやっていることは先程の英語版Wikipediaにある通りのことですが、「フィールド蓄積」ノードを使って効率的にベクトルのノルムを求めていることがポイントです
「Squared」は転置のグループを作って積を計算させることでも実現できますが、特別に用意してしまったほうが高速なので専用のグループを作成しました
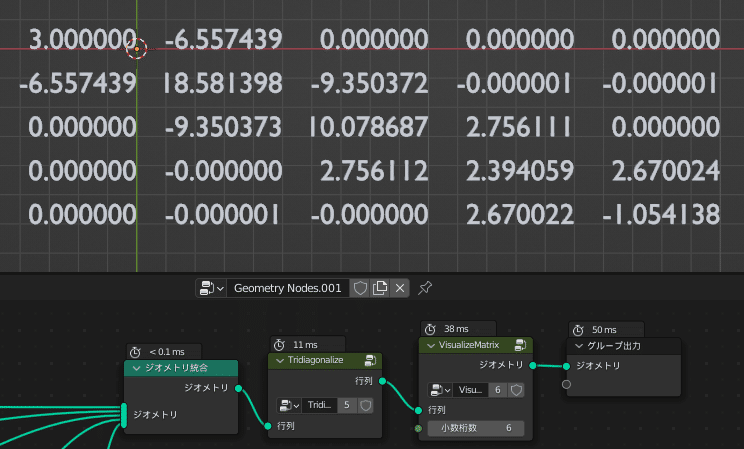
では、実際に三重対角化を試してみます
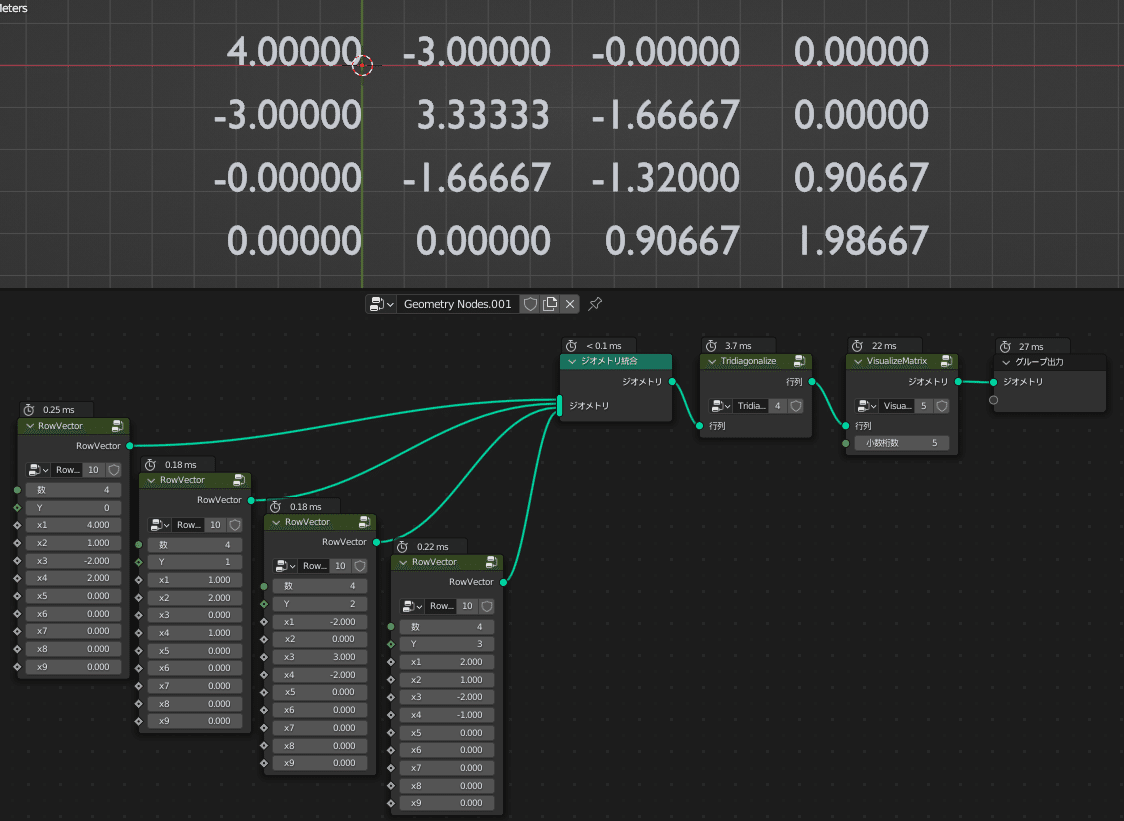
入力の行列は先程のWikipediaと同じ値にしたので確認が容易です
確かに三重対角化はうまくいってそうです

QR法
三重対角化もできたので次はQR法です
QR法は行列をQR分解して、RとQの積を計算し、それを更にQRに分解して、またRとQの積を計算し…という反復を繰り返すといつの間にか対角に固有値が並んでいく(しかも固有値の絶対値の大きさの順に並ぶ)というものです
固有値の絶対値が小さいものから収束していくので、
今回の用途には非常に都合が良いです
今回は最小固有値さえ求めれば良いので行列の右下要素が収束したら(=float精度の限界に達したら)反復をやめることにします
QR分解にはまたしてもHouseholder変換を使うことにします
それでは、QR法を実装したグループがこちらです
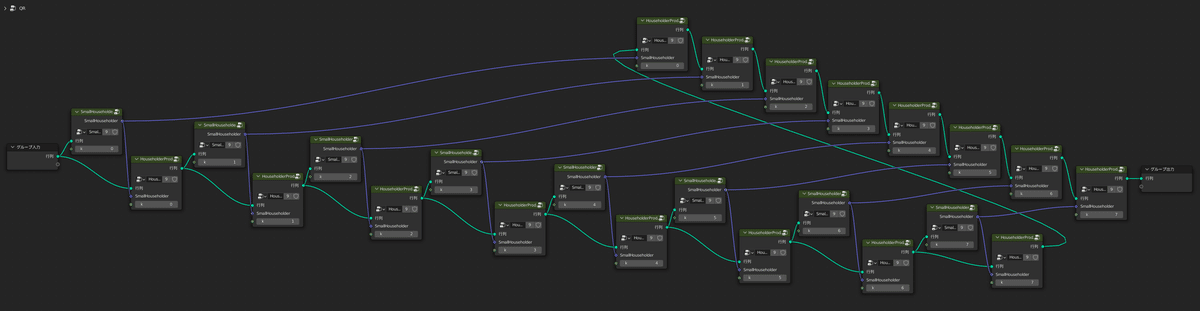
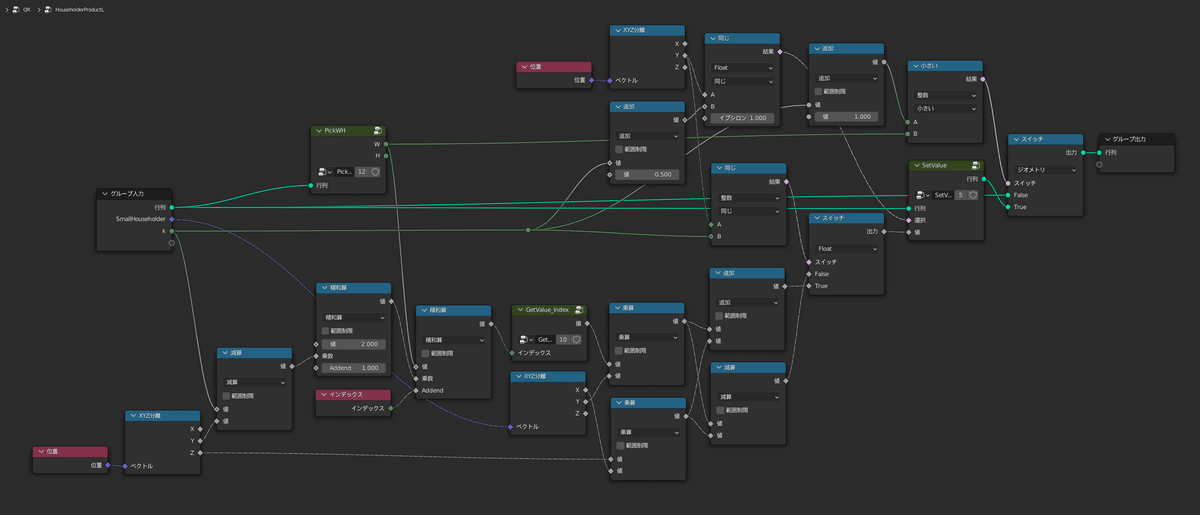
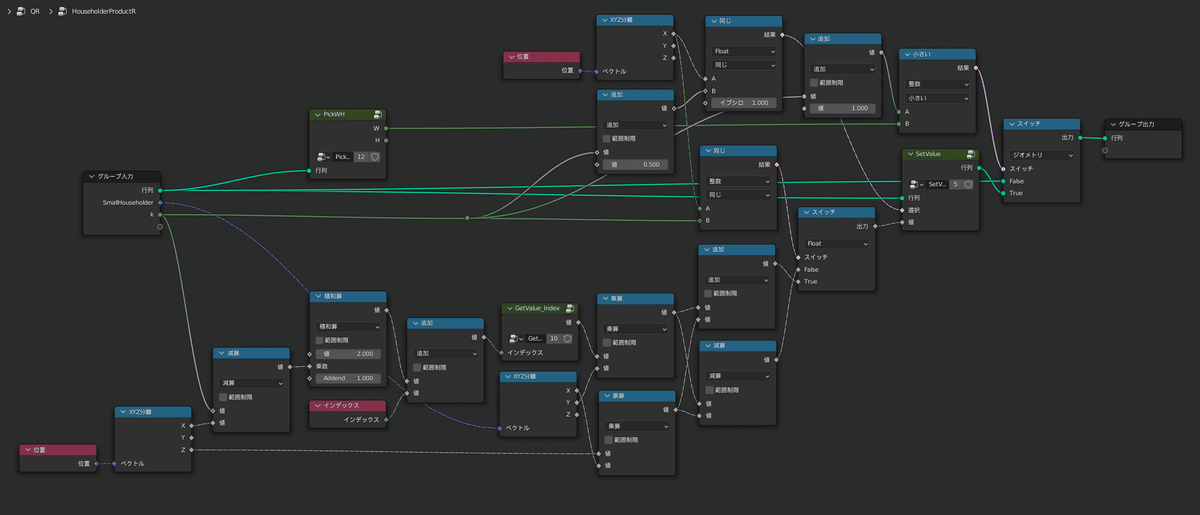
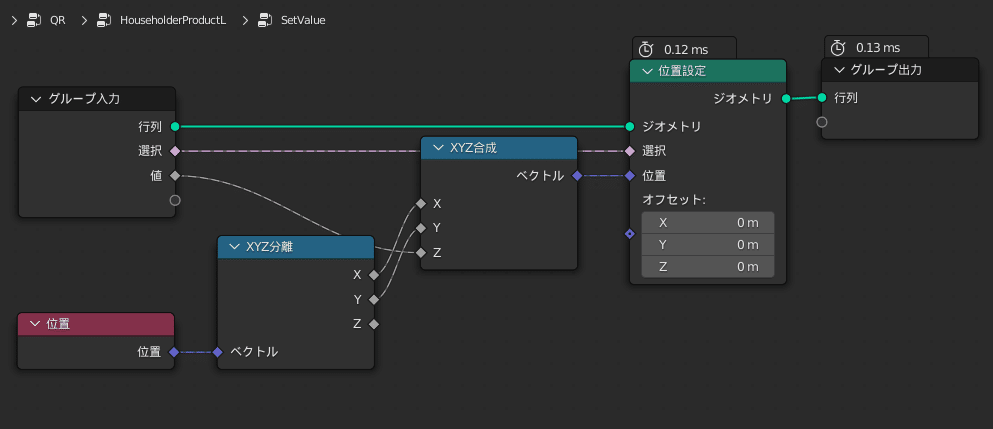
ここではHouseholder行列をBlender標準の「ベクトル」で表現しているのがポイントになっています
というのも、先程三重対角化を行ったおかげで2×2のHouseholder行列を高々8回掛ければQR分解が済み、なおかつ2×2のHouseholder行列は、
$$
\begin{pmatrix}
a & b \\
b & -a \\
\end{pmatrix}
$$
という形をしており、実数2個だけあれば行列全体をすぐ復元できます
この2×2のHouseholder行列を扱うにあたってジオメトリを使わなくてもベクトルで十分というわけです
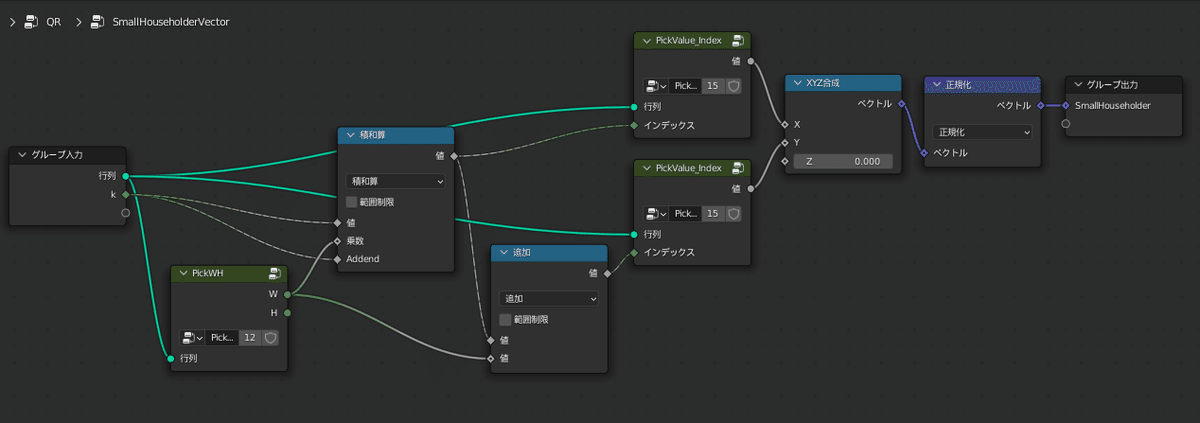
さらにベクトルを使うもう一つの利点は、
三重対角行列の対角要素 $${a}$$ と、そのすぐ下の要素 $${b}$$ から構成されたベクトル $${(a, b, 0)}$$ を「正規化」ノードで正規化してやるだけで目的のHouseholder行列を表すベクトルが完成するというお手軽さです
こうして得られたHouseholder行列(を表すベクトル)を、左から$${n-1}$$回掛け、その後右からも順番に$${n-1}$$回かければQR法の1ステップが完了します
では、実際に試してみます
今回の例は次のような行列を用います

右下の要素が「-0.828692…」に近づけば成功です
右下の要素にご注目ください!
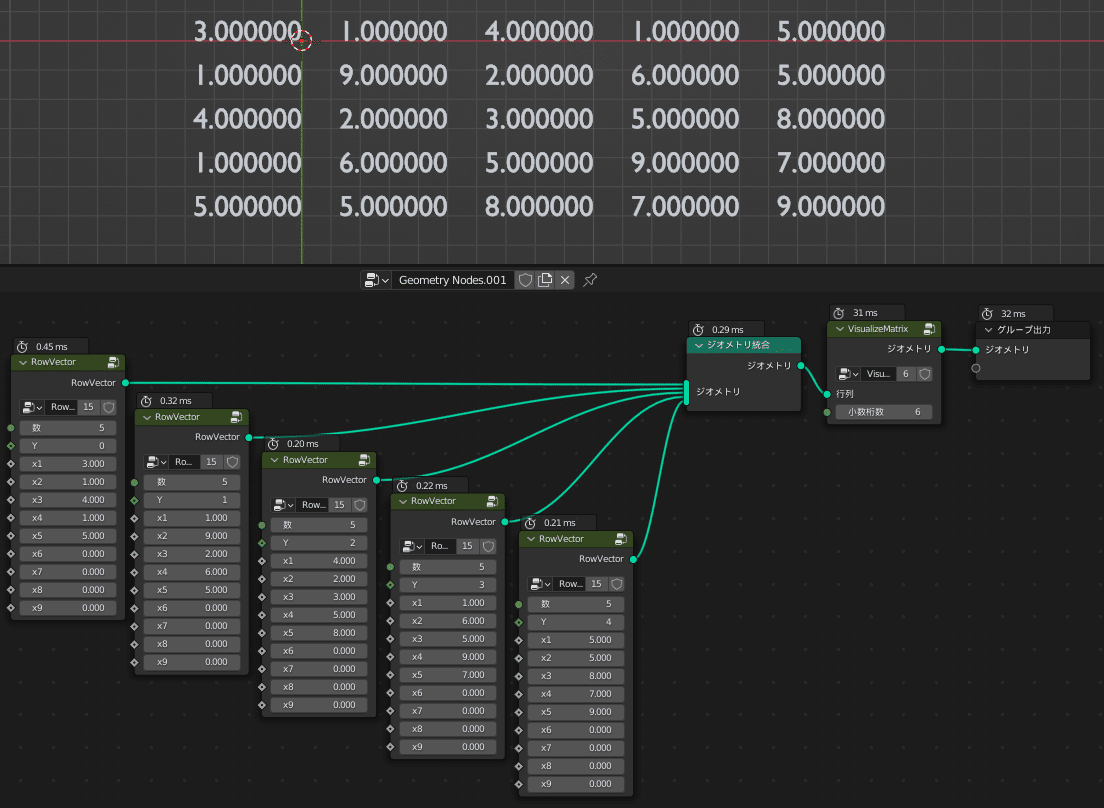
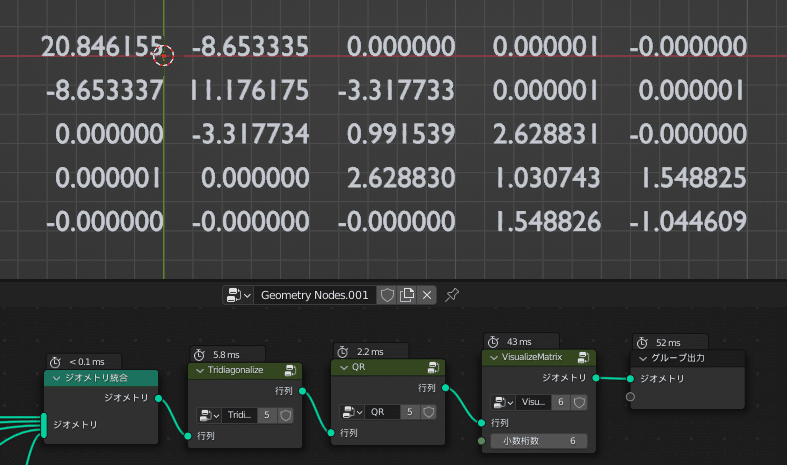

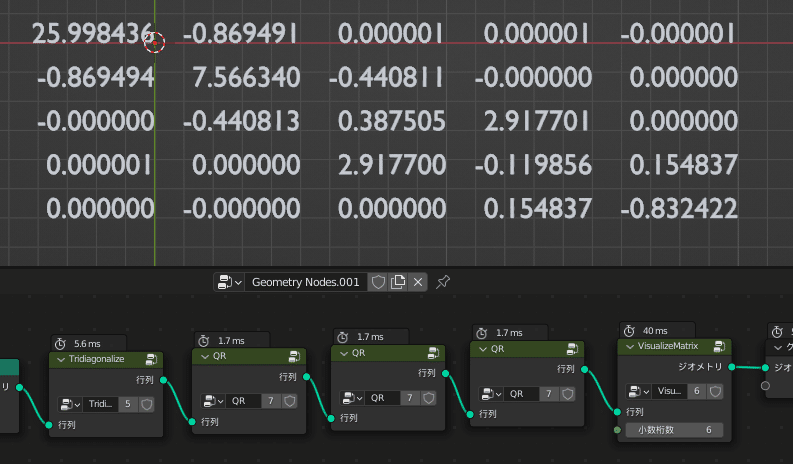
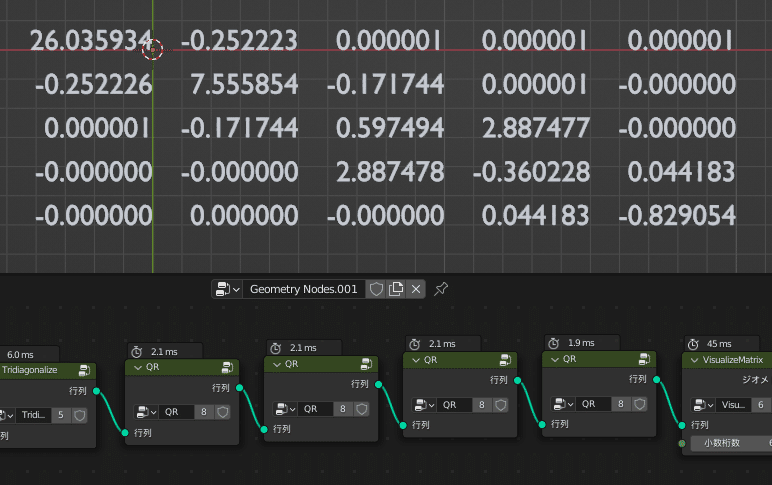
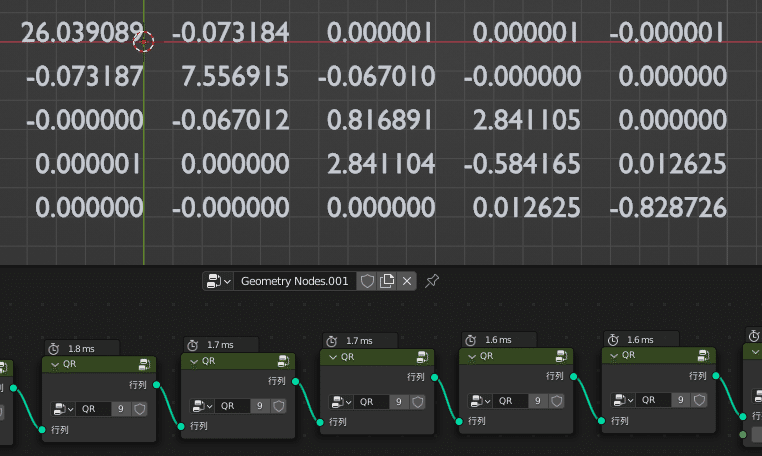

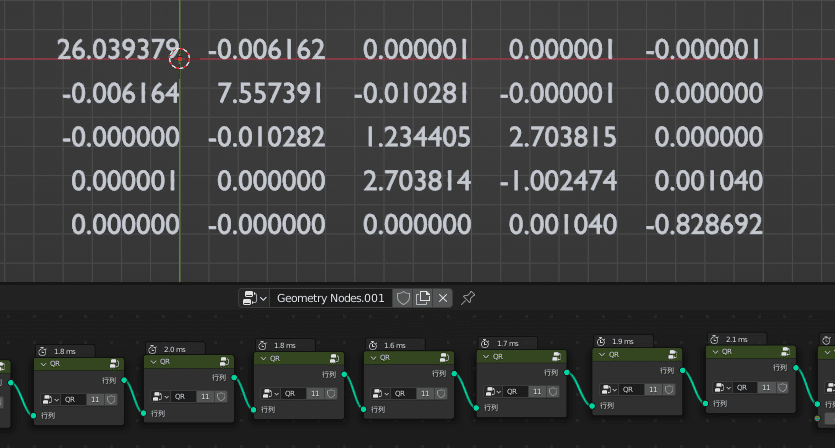
この検証では6回で最小固有値を小数点以下第6位まで求めることができました!
QR法のグループは正しく動作しているようです
これでもなかなか満足なのですが、もっと高速化する方法があります
Wilkinsonの移動法による原点移動
一般的な話として、「行列の対角要素から値μを引くと、固有値もμだけずれる」ということが知られています
そして、QR法は右下要素の絶対値が小さいほど収束が早まります
つまり、適切なμを引いて右下要素の絶対値が小さくなるようにしておけば、収束が早まることが期待できます
(固有値がずれてしまいますが、もちろん、μ引いたことを覚えていれば復元できます)
このμは右下の2×2小行列の固有値のうち、右下要素に近いものを選択すると良いことが知られており、「Wilkinsonの移動法」と呼ばれています
2×2小行列の固有値は二次方程式の解の公式よりすぐ求めることができます
以上を踏まえてQR法を実行前にμを引き、QR法実行後にμを足すという処理を組んだグループがこちらです
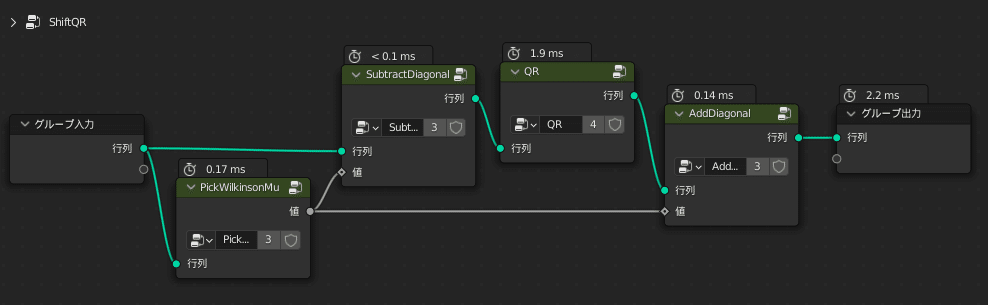
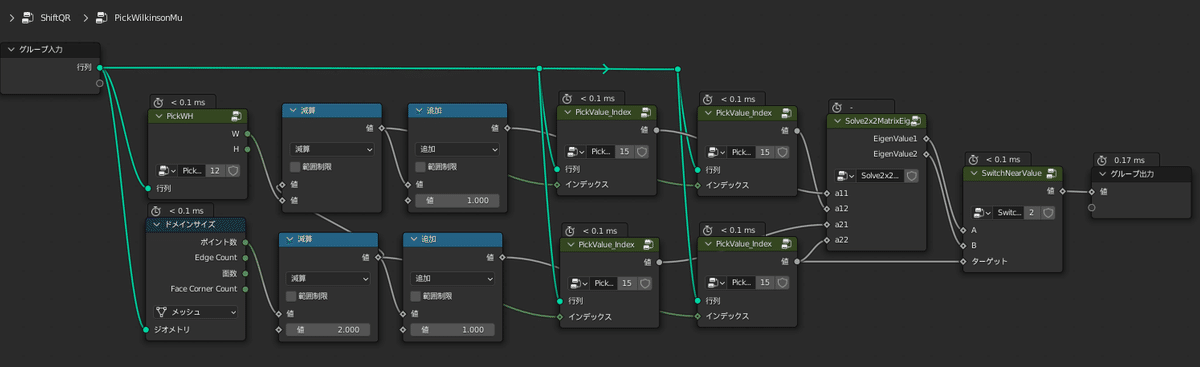
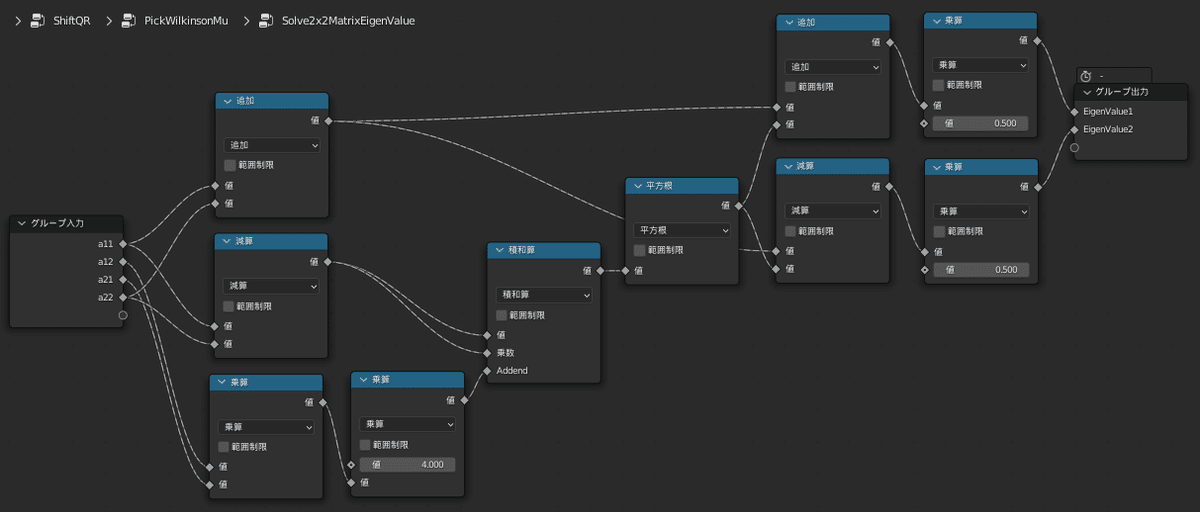
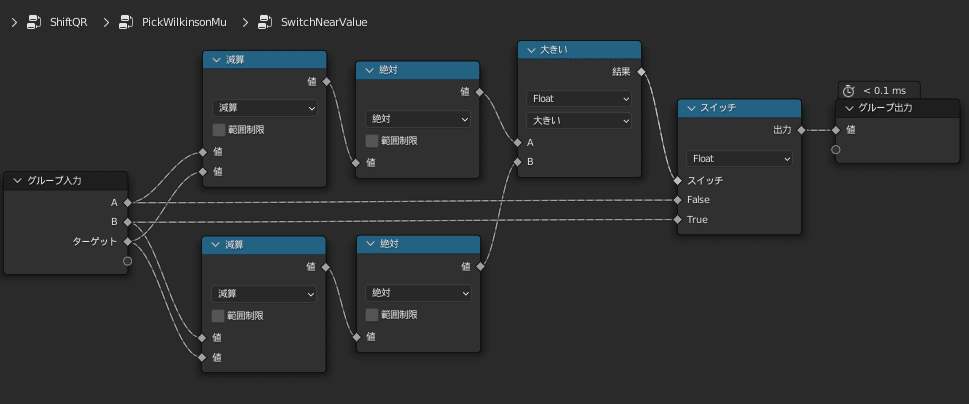


この節ではわりと自明なことしかしてないので、
早速原点移動付きQR法の威力を見てみましょう
原点付きQR法では一旦通常のQR法を1~2回程度用いて固有値をある程度"分離"してから用いていくというのが一般的なようです
従って、1回目は通常のQR法、それ以降は原点移動付きQR法を用いていくことにします



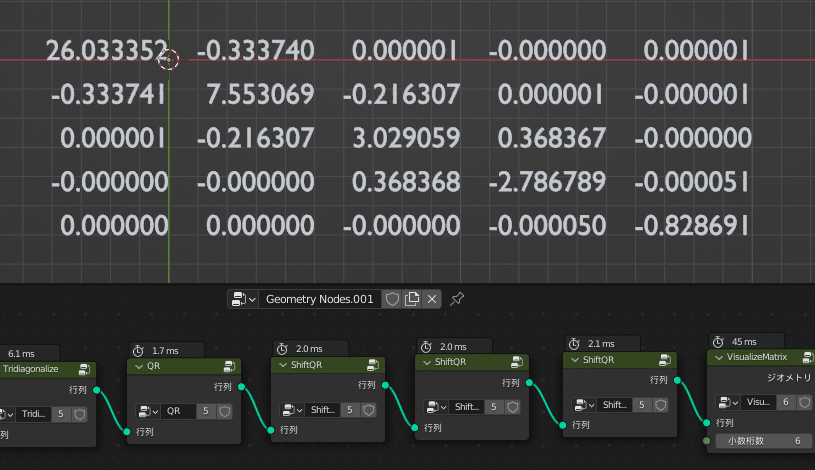

というわけで、QR法だけでは6回程度必要な水準に、計4回で到達することができました!
さらに、よく見ると先程QR法だけで行ったときと異なり、
右下要素のひとつ左上の「-2.808445」という値も2番目に小さい固有値「-2.81005…」にかなり近づいていることや、
一番下と一番右の列は、右下の要素を除いて全て0とみなせる値になっていることもわかります
固有値をすべて求めたい場合はこの時点で行列の次元を一つ減らして次に小さな固有値(ここでは「-2.81005…」のこと)を求めていくステップに移り、それを繰り返していくことで効率的に全ての固有値を求めることができます
これを「減次」といいます
今回は最小固有値さえ求まれば良いのでやる必要はないのですが、
せっかくなので減次もやってみましょう
減次


シンプルなグループですね
これをさっきの原点移動付きQR法で求めた行列に対して使って、
「原点移動付きQR法」と「減次」を交互に繰り返してみると、
意外とこれだけで結構な精度を出しつつ全ての固有値が求まることがわかります

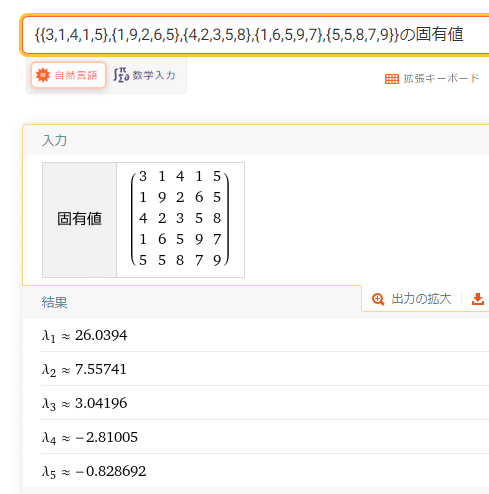
というわけで、固有値を求めることができるようになりました!
固有ベクトルを求める
固有値が求まったので、固有ベクトルも求めていきましょう
ここでは逆反復法を用いて固有ベクトルを求めることにします
$${A}$$の固有値$${λ}$$の近似値$${μ}$$と近似固有ベクトルを$${\boldsymbol{v}}$$が得られているとき、
$${(A-μI)\boldsymbol{x}=\boldsymbol{v}}$$
を解いて$${\boldsymbol{x}}$$を求めると、$${\boldsymbol{x}}$$は$${\boldsymbol{v}}$$よりも良い近似固有ベクトルとなり、$${A\boldsymbol{x}}$$と$${\boldsymbol{x}}$$との対応する成分の比は$${μ}$$よりも良い固有値$${λ}$$の近似値となる(これは一種のNewton法なので、繰り返し適用すると、初期近似が良ければ収束は非常に速い)。
以上が「逆反復法(原点移動付き逆反復法)」です
この、
$$
{(A-μI)\boldsymbol{x}=\boldsymbol{v}}
$$
という式を解くためには連立方程式を解く必要あります
連立方程式を解く効率の良い方法としては、LU分解を用いるものが知られており、この記事でもそれを採用することにします
LU分解
LU分解は下三角行列$${L}$$と上三角行列$${U}$$への分解です
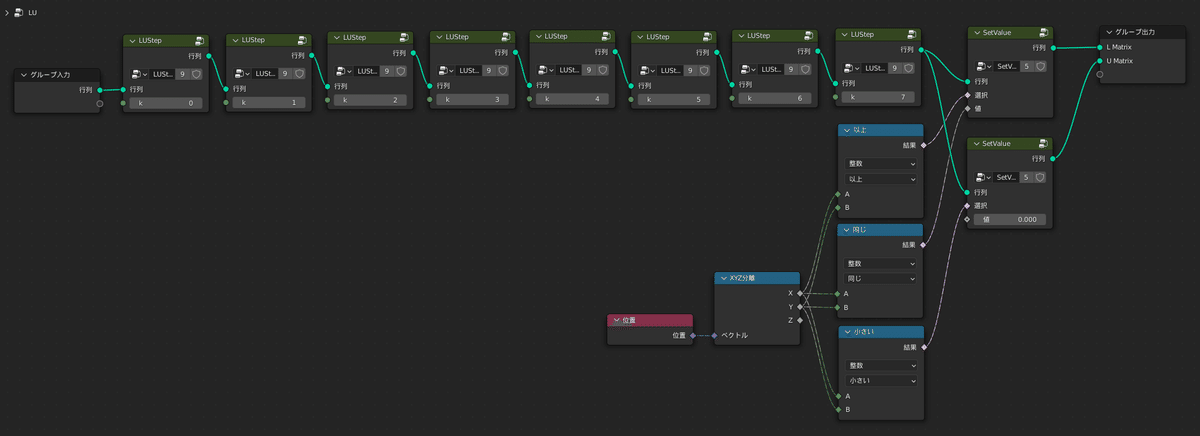
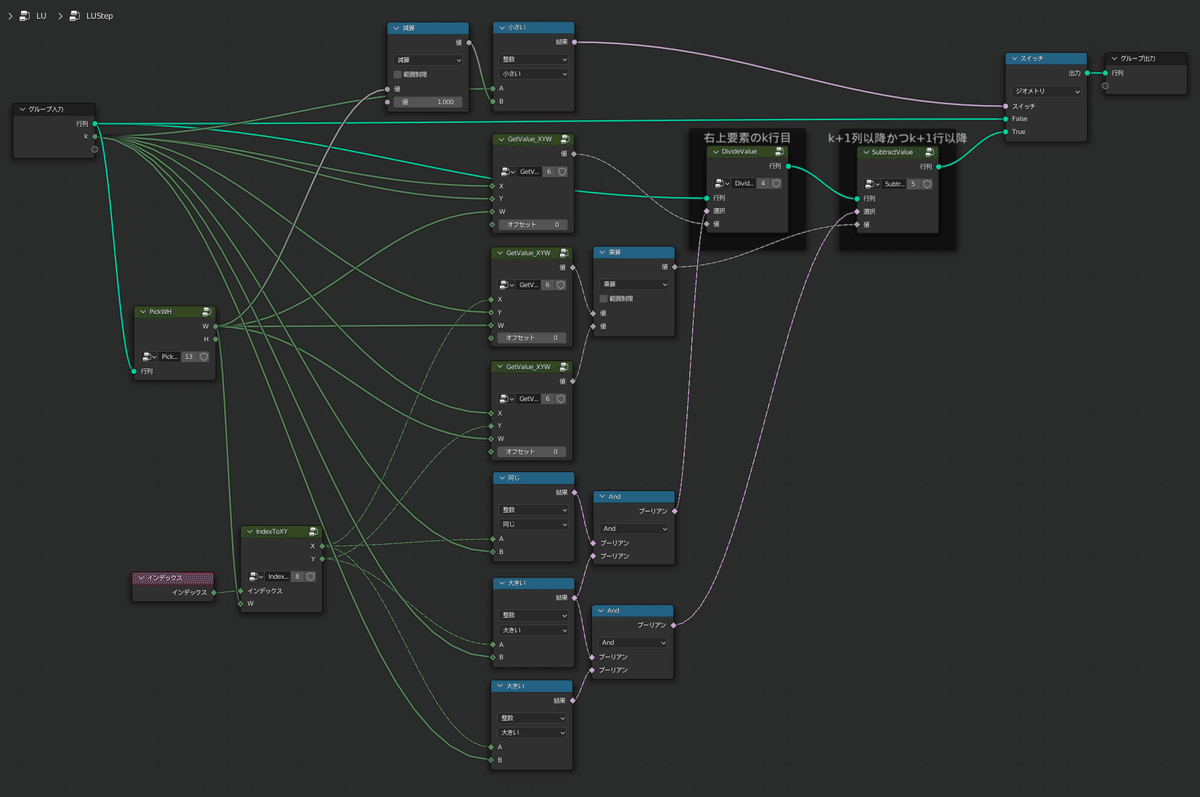
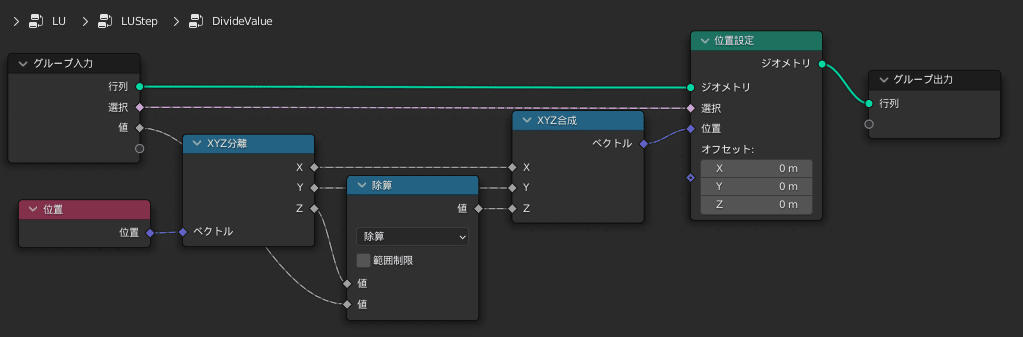
LU分解は所定の要素に対する所定の値の割り算と引き算を$${n-1}$$回繰り返すことで実現可能で、その割り算と引き算を行なっているのが「LUStep」グループです
「LU」グループでは、前半で「LUStep」を最大8回行い、最後に行列$${L}$$と$${U}$$に分離しています
実行すると確かに下三角行列と上三角行列に分解できているのがわかります


WolframAlphaだとPLUに分解されるので、
こちらのサイトで確認するのが便利です

連立方程式を解く
さて、連立方程式
$$
A\boldsymbol{x}=\boldsymbol{b}
$$
の$${\boldsymbol{x}}$$を求めたいとき、$${A=LU}$$と分解したうえで、
$$
L\boldsymbol{y}=\boldsymbol{b}
$$
を解いて$${\boldsymbol{y}}$$を求めてから、
$$
U\boldsymbol{x}=\boldsymbol{y}
$$
を解けば$${\boldsymbol{x}}$$が求まります。
$${L, U}$$が三角行列のため、比較的簡単に連立方程式を解くことができる点がポイントです
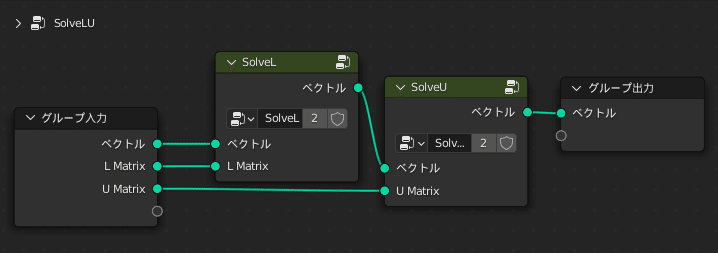
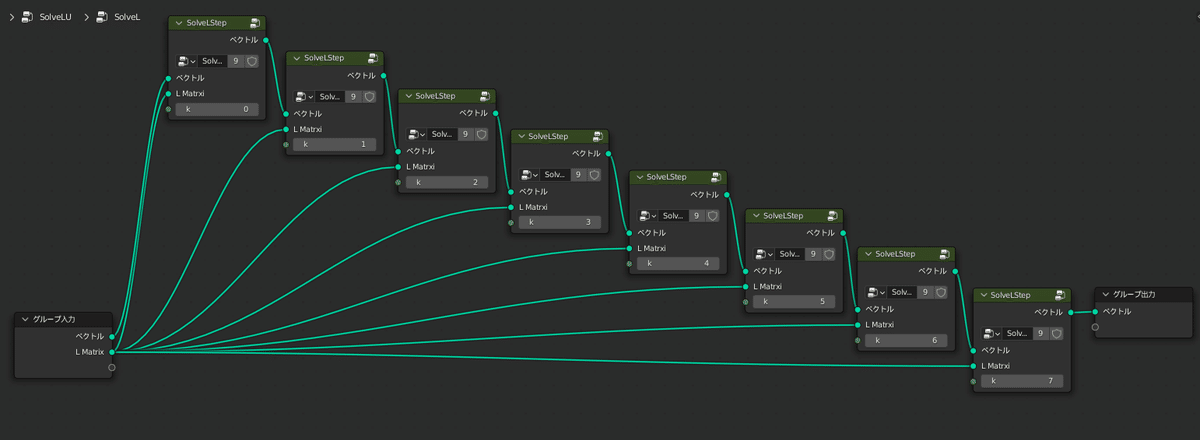

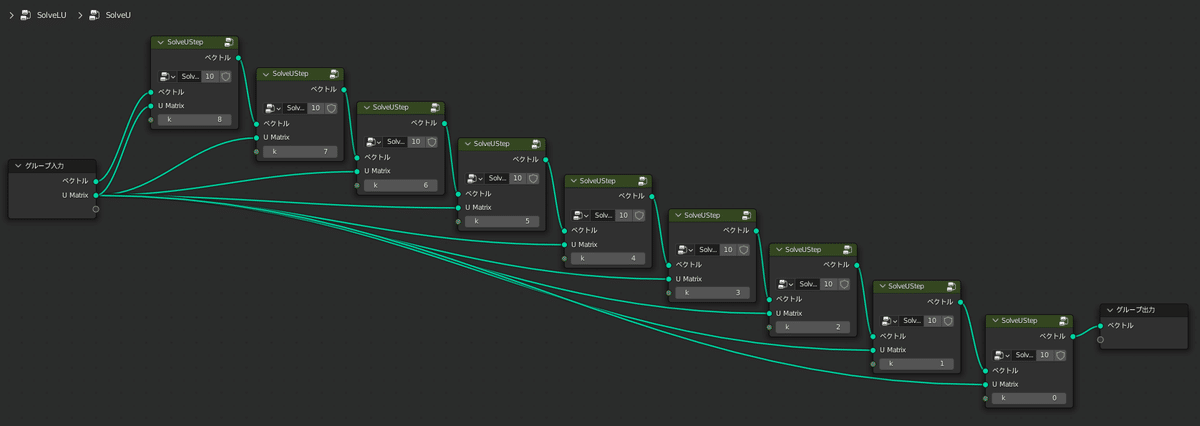

では実行してみましょう
先程の最小固有値をもとの行列の対角要素から引き、LU分解をして連立方程式を解きます

初期値のベクトルは適当に(1, 0, 0, 0, 0)としました

値が一致しませんが、WolframAlphaではベクトルの最後の要素が1になるように正規化しているためです(固有ベクトルは定数倍の自由がある)
従って正規化の処理をしてやれば近しい値になるはずです
正規化

これを使って正規化をすると、…

なんと、少なくとも表示されている小数の範囲では完全に一致しています
いきなり精度が高すぎてもはや反復の必要がないですね
近似値が良ければ逆反復法の収束の速さは強力です
反復数を色々試す
今のところ固有値を求めるのにQR法1回+原点移動付きQR法4回、固有ベクトルを求めるのに逆反復法1回でやっています
試しにここから原点移動付きQR法を1回減らしても求まる固有ベクトルの精度にはほとんど影響が出ないことがわかります

さらに減らすと、流石に値が変化しましたが、用途によってはこれでも十分な精度でしょう

ちなみに少なくとも今回の入力値の場合、
QR+ShiftQR+ShiftQRよりも、QR+QR+ShiftQRの方が精度が高いようです

ShiftQRを更に一つ削って代わりにSolveLUを増やしても良いでしょう

なんならもういっそ、固有値を求めた流れを完全に取っ払って、SolveLUだけで戦う、というのも要求する精度によってはアリだと思います(原点移動しない逆反復法では結局、最小固有値に対する固有ベクトルが得られることになります)

こんなふうに、簡単にノードを組み替えてリアルタイムに値が反映されるのはBlenderで線形代数をやることの利点かもしれないですね(ほんとうか?)
楕円当てはめ(最小二乗法)
さて、固有値や固有ベクトルを求めたりと、線形代数っぽいことができるようになったので、ここからは応用編です
記事の冒頭でも見せたような楕円当てはめをやっていきます
楕円当てはめでは、入力するN個の2次元空間上の点
$$
(x_0,y_0), (x_1,y_1), (x_2,y_2), … , (x_{n-1},y_{n-1})
$$
から、それぞれ
$$
\boldsymbol{ξ}_k=
\left(
\begin{array}{c}
x_k^2 \\
2x_ky_k \\
y_k^2 \\
2x_k \\
2y_k \\
1
\end{array}
\right)
$$
を求めて、
$$
M = \frac{1}{N}\sum_{k=0}^{n-1} \boldsymbol{ξ}_k\boldsymbol{ξ}_k^\mathsf{T}
$$
のようにN個の$${\boldsymbol{ξ}_k}$$同士の直積の平均をとった行列$${M}$$の最小固有値に対する固有ベクトル$${A, B, C, D, E, F}$$が求まれば、
$$
Ax^2+2Bxy+Cy^2+2(Dx+Ey)+F=0
$$
が求めたかった楕円(二次曲線)になります
入力から行列を生成する
入力ジオメトリ(編集モードで編集可能なジオメトリ)で既に複数の頂点が与えられているものとすると、次のようなグループを作ることで先程の行列$${M}$$を生成できます




2層にわたって「PosToConicCoef」ノードから出力された値を「MeanOfMultiply」ノードに全ての組み合わせで乗算、
それに対して「属性統計ノード」の平均を使って平均を取る、
という流れになっています
二次曲線の係数を属性として出力
これだけでは楕円当てはめの可視化はできないので、属性を出力します
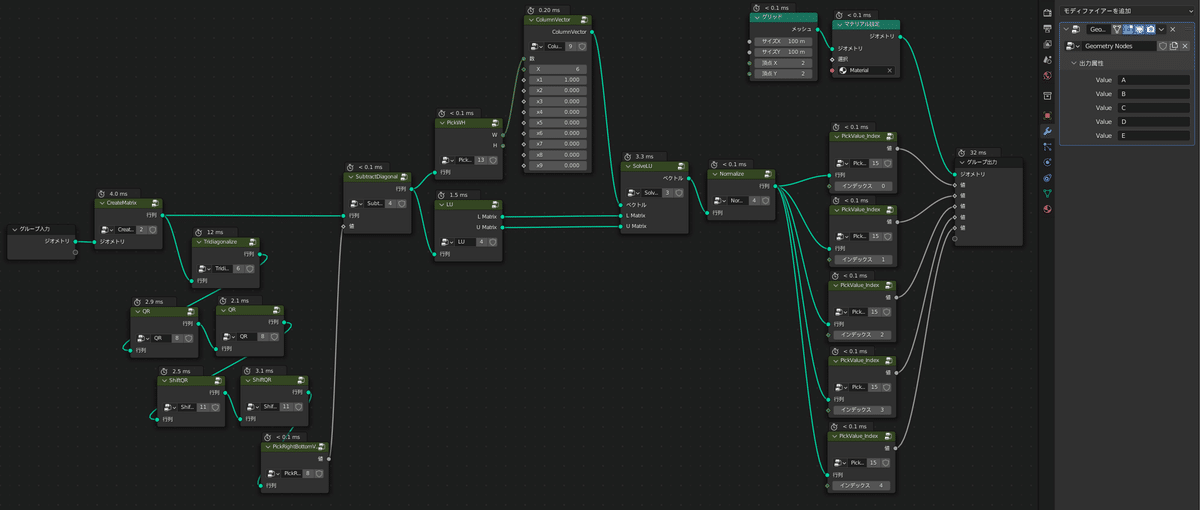
固有ベクトルジオメトリからインデックス0~5を指定して属性を出力。
上の画像のように求まった固有ベクトルから値を取り出し、それぞれ
「A」「B」「C」「D」「E」という名前の属性を出力します
(正規化しているので「F」は常に1で、出力する必要がありません)
また、表示用の板ポリもマテリアルを設定した上でジオメトリ出力に流します
属性の値からマテリアルを用いて可視化する
あとはマテリアルノードで属性の値と座標から板ポリ表面の色を決めてあげればOKです
次の画像はGeometryNodesではなく、シェーダーエディターです

あとは入力にいくつか(5個以上)の頂点を編集モードから置いてあげれば楕円当てはめの可視化ができるはずです

おめでとうございます!(できましたでしょうか?)
おわりに
この記事は以上ですが、固有値問題は幅広い応用が考えられるので、楕円当てはめ以外にも色々面白いことができると思います
リアルタイムに反映される数値を見ながらノードを繋いで行列をこねくりまわせるのは、なかなか面白ツールとして遊べるんじゃないかなと思っています
なにか間違いや質問、実際に作ってみた報告等あれば、是非Twitterからご連絡ください
参考文献
Blender Manualより「Geometry Nodes」
今回も最新のノードをたくさん使ったので大変参考になりました
数値計算の常識
年季の入った本ですが、固有値問題の解法や連立方程式解法の「まさに知りたかったところ」を非常によく突いていて大変助かりました
固有値問題解法の大まかな流れを把握するのも役に立ちました
物理のかぎしっぽより「三重対角化」「QR法」
解説が丁寧で非常に参考になりました
http://hooktail.org/computer/index.php?%BB%B0%BD%C5%C2%D0%B3%D1%B2%BD
○×的数学のお部屋より「その3 固有値と固有ベクトルを数値解析で求める」
こちらも非常に丁寧な解説で大変参考になりました
具体例で学ぶ数学より「LU分解のやり方と連立方程式を解くときのうれしさ」
LU分解による連立方程式の解法が丁寧に解説されていて助かりました
三次元コンピュータビジョン計算ハンドブック
実はこの本の第二章を理解するために(なぜか)Blenderを使って試そうとしたのが今回の取り組みのきっかけでした
CVの基礎からかなり丁寧に書かれていてとても良い本です
WolframAlpha
特に行列周りの検算で非常にお世話になりました
MatrixCalculator
非常に高機能で、WolframAlphaだと取り回しがきつい部分(クエリの長さが足りなかったりとか、LU分解とか)で大変便利でした
この記事が気に入ったらサポートをしてみませんか?
