受験で使ってはいけない？　ロピタルの定理のほんとのところ

　数学Ⅲで知っていると便利なロピタルの定理ですが，受験では使ってはいけない，裏ワザだというふうにも言われています。
　実際のところはどうなのでしょうか。

　結論からいいますと，ロピタルの定理を受験で使っても構いません。
　ただし，以下の 2 点に注意する必要があります。

1．ロピタルの定理の条件をチェックする。
2．循環論法にならないようにする。

　ロピタルの定理を使ってはいけないという主張がなされる原因は上に挙げた 2 つの注意点を守れる人が少ないからだと思います。
　この 2 つについて解説したいと思います。

ロピタルの定理の正確な内容

　まずは 1 つ目の注意点であるロピタルの定理の条件のチェックについてです。これはロピタルの定理の正確な内容は以下の通りです。

　(2) の条件はいわゆる不定形になっているという条件です。0/0 の形の不定形であるというふうにしていますが，∞/∞ の形になっていても大丈夫です。

　(1) の条件にある「（適当な）開区間」というのは，a を含む開区間を自分で設定するという意味です。この「（適当な）開区間」は (3) の条件を満たすようには設定しなければなりません。
　高校数学で使うほとんどの関数は定義域内で微分可能ですので，注意するべきは (3) の条件ということになります。

　具体例で検証してみましょう。

　条件の (1) から (4) が満たされていることをチェックした上でロピタルの定理を使用しています。(3) の条件に合致するように開区間を自分で設定しているところに注目してください。
　高校数学の範囲内で普通に解いてみると，

となるのでもちろん結果は一致します。

　ロピタルの定理は lim の先が ∞ でも使うことができます。

　∞ バージョンでもやはり (3) のチェックがネックになります。分母に三角関数が入っているときは特に慎重さが必要です。

　いずれのバージョンにしても，ロピタルの定理の結論だけを使用することはできません。4 つの条件のチェックを行った上で使用しなければならないのです。

　次に，ロピタルの定理を正しく適用したとしても使ってはいけない場面を紹介します。

循環論法に陥ってはいけない

　受験では必須で暗記しておかなければならない極限ですが，このように問題として出てきたならば，極限を求める過程を記述しなければなりません。
　この問題にロピタルの定理を適用して極限の値を求めることは確かにできます。しかし，それでは答案としてはダメです。

　循環論法に陥るからです。

　ロピタルの定理を使用するためには sin x の微分が cos x であることを使用します。しかし，sin x の微分が cos x であること証明するためにはこの極限を使用します。

　このようにロピタルの定理を使用すると極端に簡単になる問題においては循環論法の危険性があります。

ロピタルの定理は使うべきなのか

　以上より，ロピタルの定理を使用するためにはある程度の練習が必要ですし，使用できたとしても適切でない場面もあります。
　そもそも，ロピタルの定理を使用すると一気に簡単になる問題はあまり出題されません（私大の小問集合などではたまに見かける）。
　ですので，受験勉強のコストパフォマンスとしては割の良いものではありません。
　一方で，正攻法が思いつかずこのままでは白紙になるというのであれば，破れかぶれにでも使ってみたらいいんじゃないかなという程度のものです。

　ちなみに，ロピタルの定理は大学 1 年程度の数学で証明することができます。実際，私も大学に入って少し数学を勉強し始めた頃に嬉しがって証明をフォローしました。

受験数学でも「弱いロピタルの定理」が出てくる

　受験数学でもたまに「弱いロピタルの定理」が出てくることがあります。
　「弱いロピタルの定理」というのは，ロピタルの定理の条件を強くすることで高校数学の範囲内でも十分に理解可能なものにした定理です。

　2 つ目の ＝ は微分の定義式です。

　今回，この記事を書こうと思ったきっかけは，生徒が持っていた問題集で弱いロピタルの定理を使用していたところを質問されたことです。
　この式変形の発想はどこから出てきたのですかということでしたので，ロピタルの定理やその周辺の話をしました。

　高校数学の範囲だから範囲でないからなどという小さな話でとやかくいうのではなく，この定理面白いな使ってみたいなと思うのなら，ぜひ深く学んでほしいと思います。
　指導者側としてもそのような生徒の芽を摘まないようにしていきたいものです。

追記

　質問された問題は次のものです。

　解説では次のようなことをしていました。

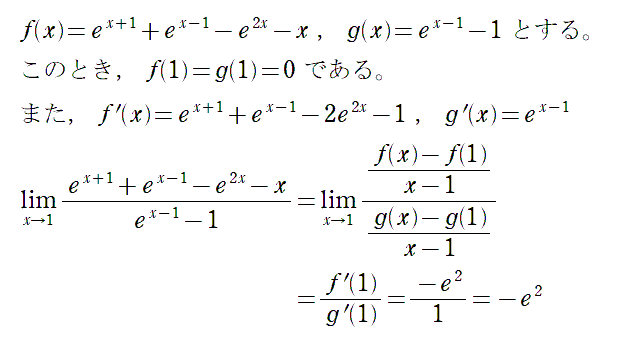
　この式変形を見て，生徒はロピタルの定理を使っているのじゃないかと思ったようです。これは先程の「弱いロピタルの定理」です。
　初めてこの式変形を見たのなら，意味はわかってもどこからこの発想が出てきたのかわかりませんね。