流体力学　２次元ポテンシャル流れ

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第５回目は，第２回目と第4回目でネタにした「速度ポテンシャル」と「流れ関数」のまとめとして，「2次元ポテンシャル流れ」をかいていきたいと思います。

（１）まとめの下準備（コーシー・リーマンの微分方程式）

　過去の記事に，「速度ポテンシャル」と「流れ関数」を取り上げましたが，まだ見ていない方は，以下の記事を見てみてください！

　さて，まとめるといったのに，なぜいまさら「下準備」なのでしょうか。実は，今までやっていた「速度ポテンシャル」も「流れ関数」もあとにかく理論が成立しないとできない，というよりそもそも議論にすらならないのです。

　私は，数学の専門家ではないので，数学的な厳密な話はしませんが，それでも大学の解析学で扱う「複素関数」に触れなければなりません。
　今回は，「速度ポテンシャル」と「流れ関数」がなぜ「複素数平面」で議論していたのかを説明します。（この話は，あえて過去の記事でも触れていないので，そのときに気づいていた方は本当によく勉強している，あるいはよく理解している方だと思います。）

　では，複素関数の微分について軽くおさえましょう。まず，図１に示すように，複素平面上（又は，z平面上）に任意の１点（点z0）を考えましょう。

図1　z0の領域について

　このとき，点z0に対して，点zが式（１）を満たすと，

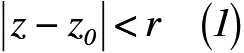
が成立します。

　z0を中心とする半径rの円の内部には，とある「領域」ができることが分かります。この複素数平面の集合の領域は，２つの条件が必要で，その条件を箇条書きで以下に示します。

（Ⅰ）開集合であること（⇒集合内に任意の点が，近傍に存在すること）
（Ⅱ）連結性があること（⇒集合内の任意の２点が，折れ線で結べること）

　２つの条件が結局，何を意味するのかを書きます。

　1つ目の開集合の成立は，領域の境界線を厳密に決める必要がなくなることです。２つ目の連結性の成立は，2つの点をどんな形であれ，線で結ぶことができることです。よって，2つの条件は，図2に示すように考えることができます。

図2　開集合と連結性について

　これより，複素平面上の点z0の極限が定義できるようになります。数学的にかくと，以下のような感じでしょうか。

「z→z0のとき，複素関数f(z)が限りなく極限値αに近づくなら，複素関数f(z)は極限値αに“収束する”」

　もし，この極限が成立すると，式（２）のように表せます。

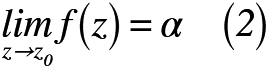
　式（２）に合わせて，複素関数f(z)からf(z0)になるとき，z=z0で「連続」が成立すれば，「複素関数f(z)がz0のある領域のすべての点で微分可能となる」ことが知られています。

　複素関数の専門用語では，これを「正則（せいそく）」といいます！

　つまり，複素関数がとある領域で微分可能なら，「正則」というわけですが，なぜこれが大事なのでしょうか。
　ここで，重要かつ注意なのが「通常」の微分と「複素関数」の微分は全く違うということです！

　高校数学の微分積分を覚えている方は，きっとこのように言われたはずです。

「微分とは，関数の傾きを求めること」だ！

　この記憶がある方は大変素晴らしいですが，複素関数の微分は実は様子が少し異なるのです。図３に「通常」の微分と「複素関数」の微分についてそれぞれ示します。

図3　「通常」の微分と「複素関数」の微分について（左：通常，右：複素関数）

　この図3が，結論です！
　通常の微分は，「関数の傾き」を求めることで間違いないのですが，複素関数の微分は，「とある領域のある任意の点zが点z0に近づく」ことなのです！

　速度ポテンシャルでもかきましたが，流体粒子の運動の状態を数学的に記述するには，動いた後の状態を予測することが非常に重要です。
　でも，流体粒子がどこに動くかはよくわからないので，適当な場所に動いたと仮定します。ただ，残念ながらあくまでも仮定ですから，流体粒子の位置が多少ズレていたことを許容できる寛容さも必要なのです。

　要するに，流体粒子の運動は複素関数で記述でき，かつ関数が微分できれば，動いた後の流体粒子の運動の様子を記述できることになります！そして，それができるのが「複素関数」だったというわけです。

　ここまで，なかなか難しい話でしたが，残念ながらまだ続きます。

　ここで，大事なのはどうやって複素関数が「連続」かつ「微分可能」を調べるかです。
　
　式（２）のように極限値が分かれば微分できることになりますが，その極限値を求めることは，流体粒子の運動の様子に置き換えると，「動いた後の位置」に他なりません。つまり，式（２）を実現させるには，「動く前」から粒子の運動の様子が分かっていることが必要になります（そんなの無理に決まっているわ…）。

　では，もうここから進めないのでしょうか？
　実はそんなことはなく，チートとのいえるべき裏技のようなものが存在します。それが「コーシー・リーマンの微分方程式」です！
　数学的な証明は今回省きますが，いわゆる定義を以下に示します。

「領域内で定義された複素数z=x+iyの複素関数f(z)=u(x, y)+iv(x, y)が正則」ならば，式（３）が成立します。

　この式（３）が「コーシー・リーマンの微分方程式」です。そして，複素関数f(z)の導関数f’(z)［複素関数の微分した関数のこと］は，式（４）のように表されます。

　先ほどの「コーシー・リーマンの微分方程式」が成立すると，連続な偏導関数であることが条件ではありますが，とある領域で正則となることが知られています。
　そして，今まで記事にしてきた「速度ポテンシャル」も「流れ関数」もこの理論が成立することを前提としていたのです。

　ここまでお付き合いいただき，本当にお疲れ様です。では，本題に行きましょう！

（２）２次元ポテンシャル流れ

　過去の記事で紹介した速度ポテンシャルと流れ関数は，渦がなくとも存在することが分かっています。
　今回も2次元流れを仮定しましょう。任意の1点のｘ，ｙ方向の速度成分をそれぞれu，ｖとしたとき，非圧縮性流体の渦無し流れを仮定すると，速度ポテンシャルφと流れ関数ψは，式（５）のように表せます（過去の記事で取り上げた式を再掲載してます）。

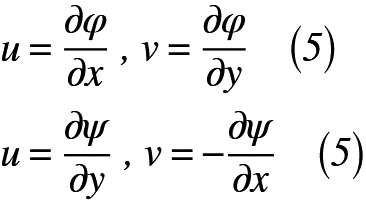
　式（５）をu，ｖにまとめると，式（６）のように表せます。

　式（６）が流体力学で使われるコーシー・リーマンの微分方程式なのです。ここで，突然ですが，非圧縮性流体の連続方程式と渦無し流れの条件式を式（７）にそれぞれ示します。

　式（７）に式（５）を代入すると，式（８）のように表せます。

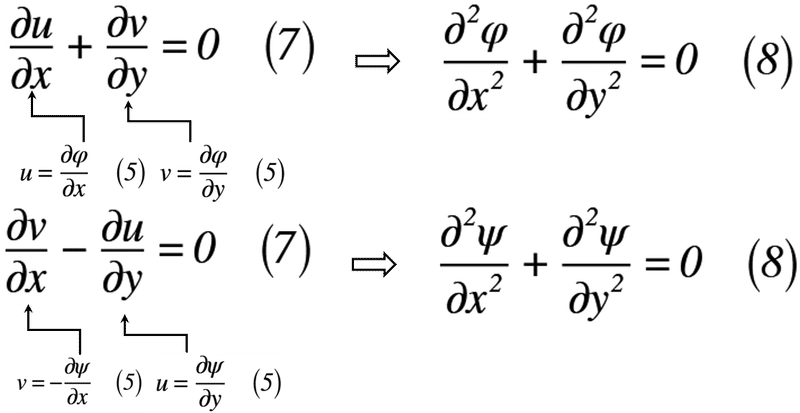
　この式（８）が「ラプラスの微分方程式」といいます。

　実は，教科書ではここまでは紹介しますが，その後の説明が意外とないまま，いきなり図を描くようになります（筆者は，ポテンシャル流れ＝図を方眼紙に書くものと思っていた時期がありました…）。
　意外とラプラスの微分方程式は大事なのですが，それは次に書きます。いよいよ「まとめ」の集大成です！

（３）速度ポテンシャルと流れ関数の関係とは

　先ほどは，速度ポテンシャルと流れ関数をつなぐ「コーシー・リーマンの微分方程式」について取り扱いましたが，この２つの関数があれば，2次元平面を流れる流体の運動の様子をグラフ化できます。
　しかし，グラフにする前に押さえておきたいのは，「数学的に正しい」ことと「速度ポテンシャルと流れ関数の幾何学関係」の２つです。

　まず，「数学的に正しい」ことを証明しましょう。

　式（８）のラプラスの微分方程式が成立することで，ｘ，ｙ方向の速度成分u，ｖは一定値となります。ラプラスの微分方程式は，速度ポテンシャルφと流れ関数ψの２階微分となっていますが，ｘ，ｙ方向の速度成分u，ｖに置き換えれば，１階微分となり，その合計が零となります。

　つまり，図４に示すようにｘ，ｙ方向の速度成分u，ｖを積分すれば，その積分値は一定値となります。よって，私たちが普段使う速度（＝流速）などをそのまま使えることになります。

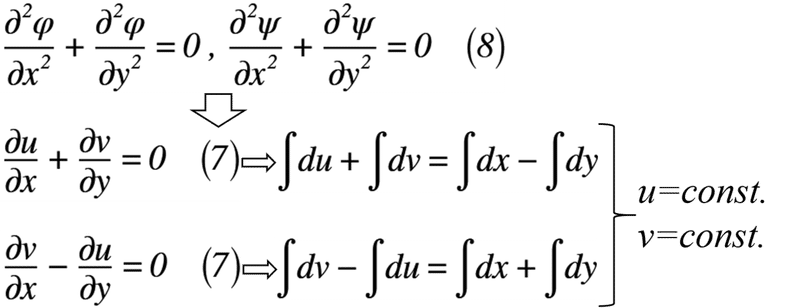
図４　ラプラスの微分方程式から一定値の算出まで

　さらに，速度ポテンシャルφと流れ関数ψについても，２階微分で表現されていますが，いずれの関数も一定値でなければ成立しません。
　そこで，速度ポテンシャルφと流れ関数ψが１階微分の形式で表せれば，これらも一定値であることが分かります。

　ここで，式（６）のコーシー・リーマンの微分方程式を用いてみると，式（９）のように表されます。

　式（９）より，速度ポテンシャルφと流れ関数ψが１階微分となるので，いずれも一定値となるので，式（１０）のように表されます。

　これより，速度ポテンシャルφと流れ関数ψの一定値が成立することで，普段使っている速度（＝流速）などを用いることができ，その出発点はラプラスの微分方程式であることが分かってもらえたかと思います。

　次に，「速度ポテンシャルと流れ関数の幾何学関係」を導きましょう。

　結論から申し上げますと，幾何学的に速度ポテンシャルφと流れ関数ψは互いに必ず直交することが知られています！では，これを証明しましょう。

【証明】等ポテンシャル線φ=const.と流線ψ=const.が互いに直交すること

（解）速度ポテンシャルφ=const.と流れ関数ψ=const.をxについて微分すると，式（１１）と式（１２）のように表されます。

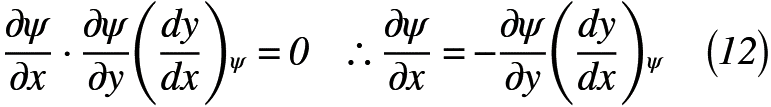
　式（１１）×式（１２）とすると，式（１３）のように表されます。

　ここで，式（６）のコーシー・リーマンの微分方程式を用いて，式（１４）のように書き換えます。

　ここで，式（１４）を式（１３）に代入すると，式（１５）が得られます。

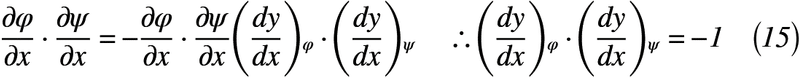
　式（１５）によって，φ=const.とψ=const.の曲線は必ず直交することが分かりました！

（４）まとめ

　今回の記事のまとめを以下に示します。
（１）複素関数の微分は，関数の傾きを求めることではなく，「とある領域の任意の点が別の点に近づく」こと意味する。
（２）コーシー・リーマンの微分方程式は，連続な偏導関数である場合は「正則」である，つまり微分可能なことが分かる。
（３）速度ポテンシャルφと流れ関数ψは，幾何学的に必ず直交する。

　以上です。最後まで閲覧頂きありがとうございました。