流体力学　渦流れと渦無し流れ

　皆様おはこんばんちは。そして、お疲れ様です。

　最近、流体力学を再度学び直してみようと思い、記事にしてみます。
　とは言え、皆様には少々学び直したい背景を言ってみたくなったので、時間のある人は読んで見てください。
　一方、今回の内容を知りたい人は下の目次（１）から探してみて下さい。

（０）学び直しの理由

　そもそも何でいまさら流体力学なのかは、置いておいてください。今回のタイトルは「渦流れと渦無し流れ」ですが、ここで皆様ご存じでしょうか？

 　大学・高専で扱う流体力学は、「実はさらに細分化されていること」を！
　

　細かい細分化の話をする気はありませんが、大学・高専で扱う流体力学は大きく４つに細分化されます。それをざっくりした説明ですが、以下に示します。

（１）水力学；主に液体である「水」を対象に、水が通過した配管内外の状態量を算出する学問。
（２）理想気体；主に気体である「空気」を対象に、空気が実際の物体にあたったときの流体粒子のふるまいや実際の空気の流れを解析する学問。
（３）粘性流体；主に流体である「水」、「空気」を対象に、配管内外を通過する「水」の状態量や物体を通過する「空気」をより詳細に解析し、より正確な状態量や流れを理解するための学問。
（４）圧縮性流体；主に「空気」を中心にとてつもなく高い速度、圧力や温度が発生する状況を想定したときの流体の状態量や流れを解析する学問。

　以上がざっくりした説明です（偉い先生がこんな記事を見たらさぞ怒ることでしょうね…）。
　大学・高専にも様々な事情があるので、細かいことは省きますが、ここでは、私が感じたあくまでも個人的な見解を伝えておきます。

　実は、多くの大学では「理想流体」と「粘性流体」をメインに取り上げるのに対して、高専では「水力学」と「粘性流体」を流体力学の講義として取り上げることが多いように思います。

　なぜこんなことになっているかについては、またの機会にしたいと思います。私の場合は「流体工学」として講義を受けましたが、「水力学」と「粘性流体」の分野しか学んでいないのです！
　本来は、高専から大学へ編入学するような場合、このような事態は避けられるはずなのですがね…。

　私は、大学院試験のために勉強した経験もありますが、「理想流体」の分野はいわゆる「独学」です。今まであってきた人にこの話をしたこともありましたが、そのときに「独学なんてすごいね」という人にも出会いました。ですが、私からすれば「専門の先生が講義してくるありがたさ」や「試験という形で自分の理解度をチェックしてくれる」こと大切さを痛感しました。

　当時、大学院試験のために勉強したときは、様々なことが後手に回って、非常に切羽詰まった状況でしたから、あの勉強では、気付かなかったことも記事にしてみようと思ったのが、学び直しのきっかけです。
　さて、長文にお付き合いいただきありがとうございました。早速、「渦流れと渦無し流れ」について書いていきます。

（１）渦の設定方法とは？

　皆様が目にする「渦」とはどのようなものでしょうか。私は「渦」というと、コーヒーにミルクを入れたときの模様みたいなものや風呂の栓を抜いたときにできるものを想像します。こんな渦の状態について、数式を立式する、あるいはモデル化をするわけですから、なかなか難しいですよね。
　そこで、詳細は省きますが、流体力学でよく使う「連続体」の考え方を説明します。

図１　物質の原子・分子の集まり

　図１に示すように、あらゆる物質は一つ一つの原子・分子の寄せ集めで構成されています。しかし、我々の視力では到底こんな原子・分子は見えません（もしかしたら、見える人は…いませんね、きっと）。
　しかも、今回知りたいのは「渦」なわけですから、原子・分子が見えるような世界を「ミクロな世界」とするなら、我々が普段見るような渦がある世界は「マクロな世界」ですよね。
　そんなとき、ミクロをマクロにするときの強引ともいえる手法をお伝えします。まずは、一つの箱（１ｍ四方の立方体）を考えます。

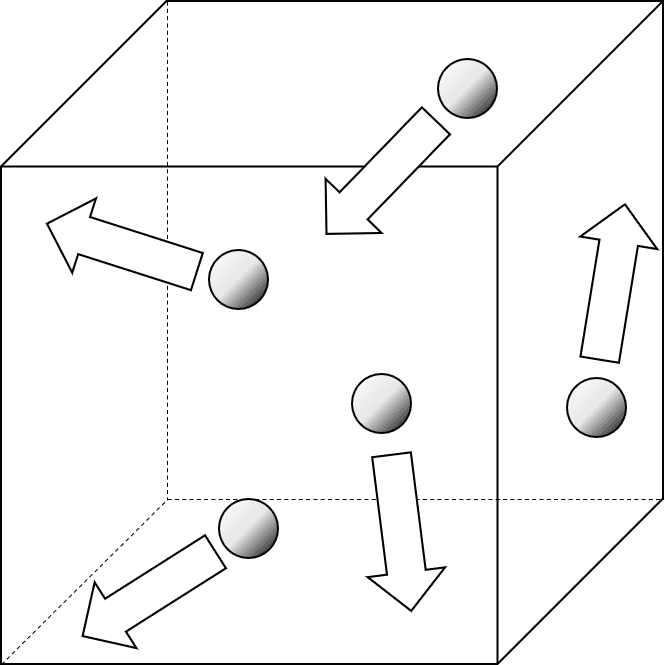
図２　原子・分子の運動の様子

　次に、この中に原子・分子があって、かつその箱の中での原子・分子の運動による影響が無視できれば、原子・分子が整列した箱が出来上がります。

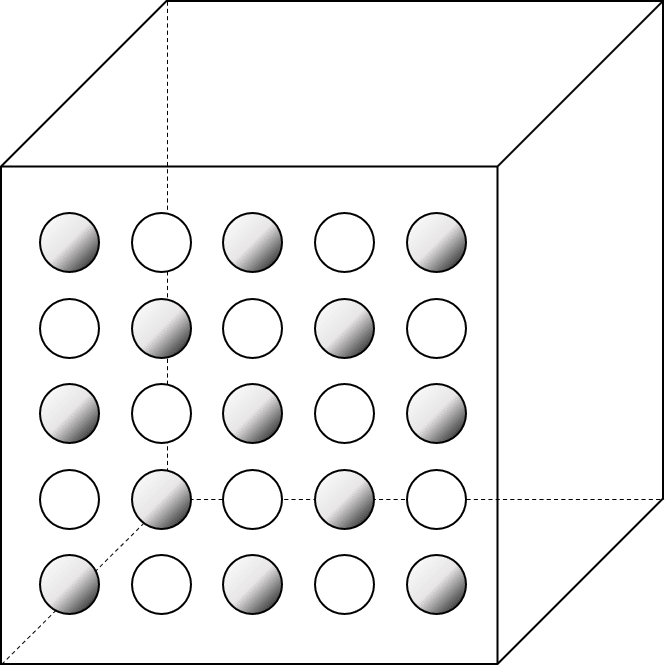
図３　連続体のイメージ

　図3に示したのが、いわゆる「連続体」です。流体力学では、なぜか「流体要素」、「微小要素」と名前を変えて呼ぶようです。
　しかし、これだけでは結局のところ、ミクロをマクロに変えるということはできても、なぜ「連続体」として使うのか？についての答えを述べていないため、意味不明かと思います。

　答えは、マクロな世界に置き換えられれば、「原子・分子の集密度（密度）や平均の速度など」が求められるためです。

　ミクロな世界のままでは「原子・分子の個々の位置や速度など」を求める必要があります。近年の科学技術の進歩によって、特殊な顕微鏡を使えば、かなり小さい物質の原子・分子が観測できる時代になりました。
　しかし今の技術をもってしても、人ひとりが余裕で入れる風呂場の水でできる渦を観測して、水やそれ以外の原子・分子の個々の観測をすべて行うことは当然不可能であり、また、たとえ観測できても「それって、今見たい現象に直接結びつくの？」と思うのが普通ではありませんか？

だからこそ、流体力学では「連続体」を使うのです！

　そして、渦の解析には、「連続体」は不可欠なのです。

（２）渦を2次元化してみると

　さて、前述した通り「連続体」について記載しましたが、それよりも渦を誰もが分かるイメージにできなければ、使うことすらままなりません。
　そこで、簡単にイメージするにはやっぱり2次元で考えるのが一番ですよね。ここでは、非圧縮性２次元流れの中に直交座標ｘ，ｙをとり、任意の一点のｘ，ｙ方向の速度成分をそれぞれu，vとおくと、以下に示すような式（１）で表せます。

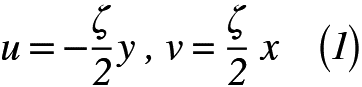
※ζの説明は後で行いますが、ここでは比例定数だと思っていてください。

　式（１）を考えると、図４に示すような2次元グラフが書けます。

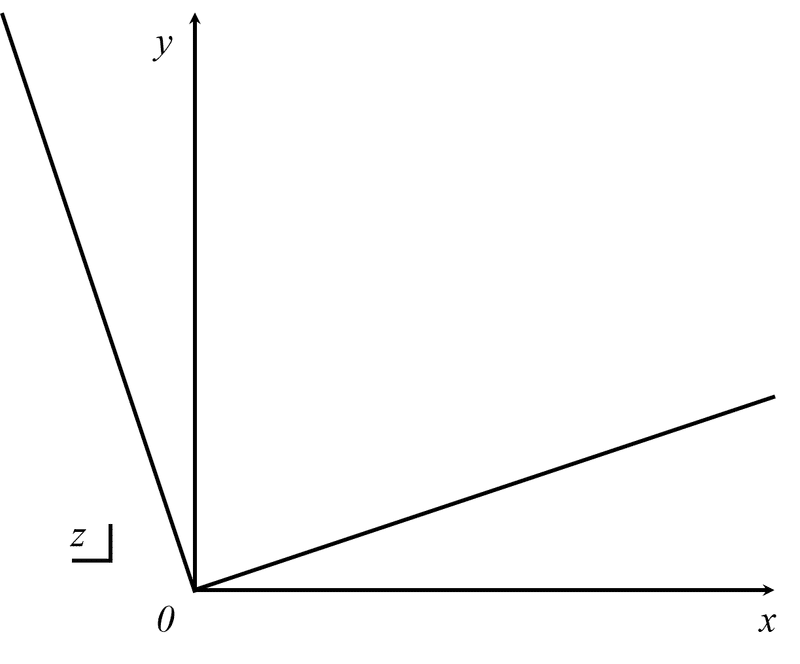
図４　xy平面の速度分布

　しかし、これでは「線」が引けただけでよくわからない、式（１）がイメージできないから結局、式（１）をなんかよくわからないけど覚えてしまう流れにしてはもったいないので、直観的に理解するために中学数学を思い出しましょう！

　中学入学後、皆様はきっと数学の科目で関数の授業を受けたことでしょう（今の要領では、中学一年の範囲です）。そのとき、関数の概要を学んだあとにｘ，ｙの座標に囲まれた中に直線を引いたのではないのでしょうか？
　そのとき、大事なことは「定規で直線を引いた」ことでもなく、「方眼紙を使った」どうかでもなく、「x、y座標に対応する点を打って」から直線を引いたことです。これを思い出せば、式（１）の見え方が変わりませんか？

　式（１）は、「x、y座標線上に流体粒子があったと仮定すれば、その粒子が動いた後の点を直線で結んだものである」と思いませんか？
　そのイメージを図5に示します。

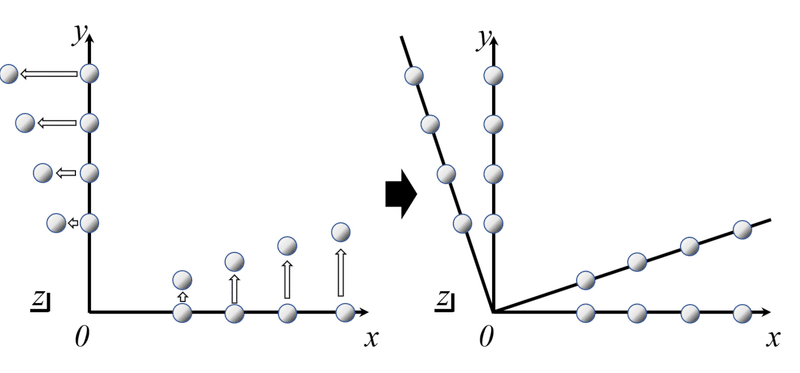
図5　流体粒子の速度分布と式（１）の意味

　これで、コーヒーにミルクを入れてかき回しているとき、渦が左周りに回っているような様子を再現できていると思いませんか？
　さらに、ここでx、y座標の中にある流体粒子が同心円状に存在すると仮定すれば、円の方程式x^2+y^2=r^2を用いることができるため、原点より半径rの距離の点における速度qは、以下に示すような式（２）で表せます。

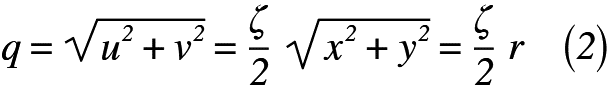
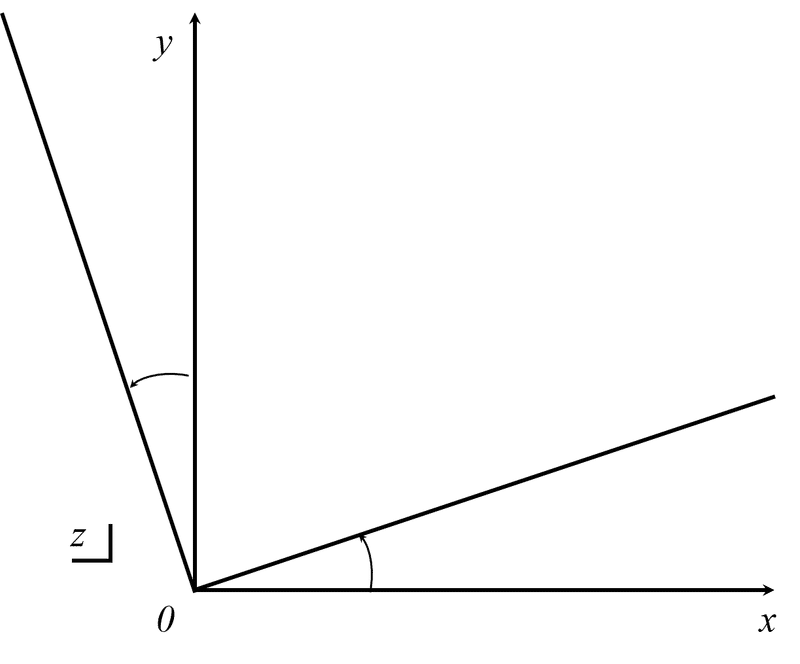
図６　角速度ζ/2だけ回転する流れ

　よって、図６に示すようにx、y座標線から式（１）まで動くときは、式（２）より角速度ζ/2だけ回転する流れが出来上がりました。

（３）渦を連続体で考えてみると

　前述では、点を流体粒子に置き換えて渦の流れを考えましたが、次は「連続体」で考えてみましょう。先ほどと同様に、非圧縮性２次元流れの中へ「連続体（微小要素ABCD）」を置くと、図７に示すようになります。

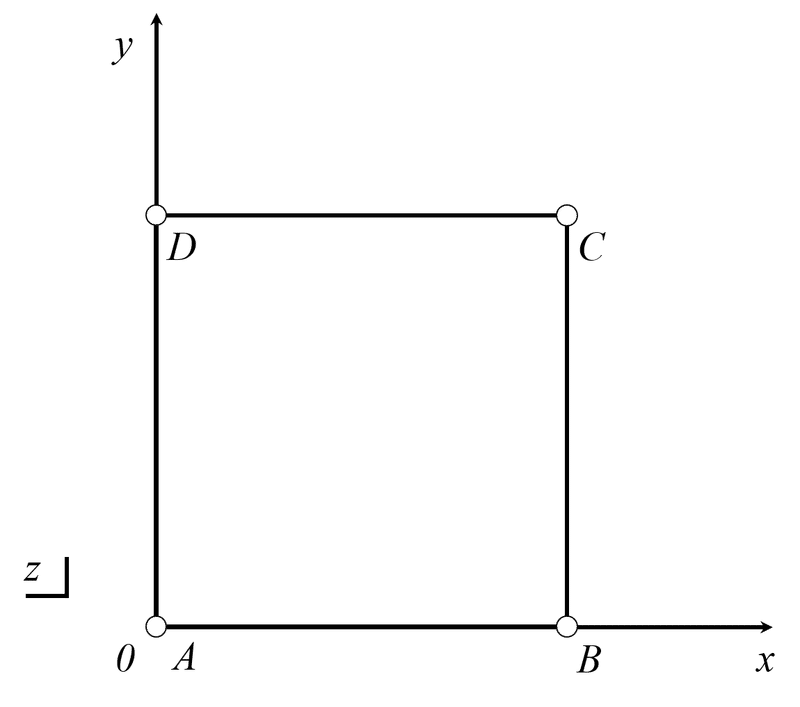
図７　xy平面における微小要素ABCD

　ここで、流体粒子が動く前と動いた後の様子と考えるのと同様に、微小要素が変化するイメージは、図８に示すように微小要素ABCDから微小要素A’B’C’D’へ回転する状態になります。

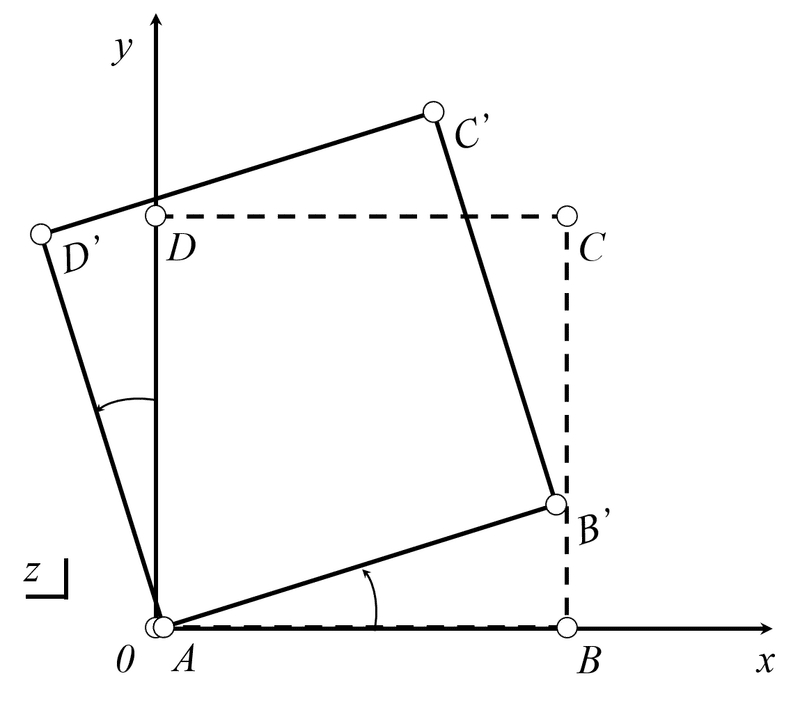
図８　角速度ζ/2だけ回転する微小要素A'B'C'D'

　でも、流体粒子から微小要素に変わったことで数学的にはどう記述すればよいのでしょうか？

　ポイントは、微小要素の線分ABが線分A’B’に、線分ADが線分A’D’に線分が変わっていることで、回転した後の線分A’B’と線分A’D’に傾きがあることです。

　ここで、高校数学の微分積分を多くの授業では、こんなことを例示で言われたはずです。（覚えていない人は、こんなことを言う人がいるんだという感じで構いません。）

微分は「関数の傾きを求めること」だ！

　かなり強引ではありますが、この考え方に基づけば、式（１）を微分した結果が、連続体の回転する流れを記述できるため、式（３）で表せます。

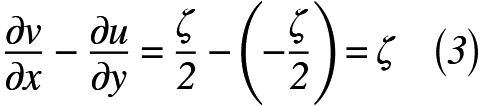
※注意；線分ABの角速度が右向きなのに対して、線分ADの角速度が左向きなので、それぞれの微分の引き算となる！

　ここで、ζは渦度と言います。式（３）がいわゆる「渦流れ」を記述する式となります。

　また、ζ=0の場合は、渦が発生していない状況となり、「渦無し流れ」となります。

（４）まとめ

長くなりましたが、今回の記事のまとめを以下に示します。
（１）渦は、「連続体」を前提に考えている。
（２）２次元グラフの直線は、流体粒子が動いた後の様子を表している。
（３）連続体を適用した場合、流体粒子と同様に考えると回転する様子を数式で表せる。

　以上です。最後まで閲覧頂きありがとうございました。