
流体力学 シュワルツ・クリストッフェルの定理
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第52回目は,「シュワルツ・クリストッフェルの定理」をについて紹介したいと思います。
(1)シュバルツ・クリストッフェルの定理とは
不特定多数の皆様はいきなり,「シュバルツ・クリストッフェルの定理って何?」となりそうなので,軽く紹介します。
いつものごとく,2人の人物が関わっているからこの定理の名前になっている訳です。
登場人物の暇人1人目は,19世紀にドイツの数学者,物理学者として活躍したエルヴィン・クリストッフェルです。電磁気に関する内容で博士号を取得した彼は,スイスにあるチューリッヒ工科大学で教授をしていたそうです。そのとき,彼が別の大学へ異動するときの後任としてきたのが,もう一人の登場人物の暇人2人目であるドイツの数学者として活躍したヘルマン・シュワルツです。
この2人は,別に師弟関係であったわけではありません。この定理に関する論文を出したのは,エルヴィン・クリストッフェルです。一方で,ヘルマン・シュワルツは教育業に熱心だったため,この定理が提唱された当時に論文を執筆していませんでしたが,この分野で多くの功績を残した業績が評価されてシュワルツの名も残ったと筆者は推察しています。
さて,当時の背景は上記の通りですが,具体的な定理の話をしましょう。
複素平面上では,等角写像が成立することは以前の投稿した記事でも紹介しておりますが,等角写像が成立する条件の1つにリーマンの写像定理があります。これを使って,本来はシュワルツ・クリストッフェルの定理を証明するそうですが,筆者にはちょっと荷が重すぎました。そこで,とある教科書を参考にした証明を紹介します。
(2)シュバルツ・クリストッフェルの定理の解釈
では,前項で取り上げたシュワルツ・クリストッフェルの定理を証明してみようと思います。今回は厳密な証明ではなく,幾何学的な証明をしていきます。
証明の前に,なぜこの定理が必要になったのかを考えましょう。今までのジューコフスキー変換では,z平面がすべて「円」を前提としておりました。つまり,円のみで成立しているとも言えます。そこで,円以外のn辺多角形でも成立すれば,形状による制約がなくなります。この制約を取っ払うことができた定理こそ,「シュバルツ・クリストッフェル(Schwarz-Christoffel,以下SC)の定理(もしくは,変換)」なのです。
よって,専門書にはこのようにかかれています。
ζ平面に示された内角α1,α2,α3,…,αnのn辺多角形ζ1,ζ2,ζ3,…,ζnの内部は式(1)が成立する。

式(1)の変換式(但し,A:複素数の定数)により,z平面の上半面に変換され,多角形の周辺はz平面のx軸上に対応し,ζ1,ζ2,ζ3,…の対応点x1,x2,x3,…はそれぞれx軸上に求められ,ζ平面のn辺多角形領域が対応する。
この式(1)を読み解くのはかなり大変ですが,「ζ平面からz平面に変換するとz平面の上半面(x軸上,もしくはx軸の正の領域)に必ず存在する」ことが書いてあります。今回は,上記の説明部分を幾何学的な証明ができるかについて確認していきます。
(3)シュバルツ・クリストッフェルの定理の証明
では,複素関数を定義していきます。定義するときに考えるのは,ζ平面にn辺多角形ができるということは,図1のようなイメージになります。
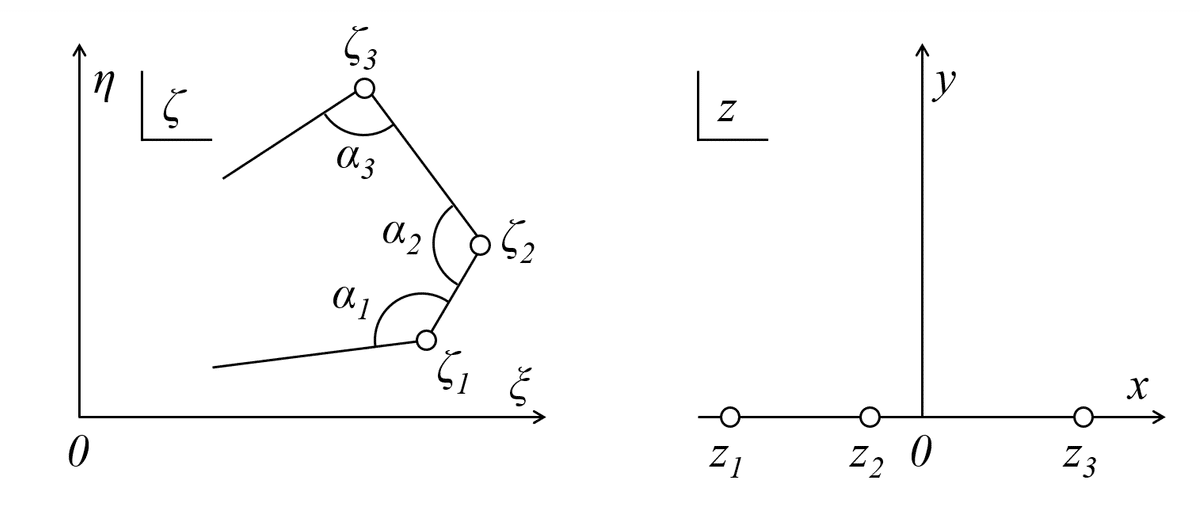
そのため,流れもこのような角度に沿った流れにする必要があるので,以前の投稿で紹介した「任意の角度を回る流れ」の考え方を使います。
よって,複素数ζは式(2)のようになります。

角度を考えた流れにしたいので,複素数ζを極座標形式にするために式(3)を使います。

ここで,式(3)を(2)に代入して,複素数zで微分すると,式(4)のようになります。

本来は,式(4)のnの値によって流れの挙動が変わりますが,今回の証明で必要なζ平面からz平面に変換すると,z平面の上半面になることを確かめるには,nを考える必要はありません。よって,nの影響を無くすために,n項を省略すると,式(5)のように表せます。

このとき,式(5)の場合の角度θの変化を考えると,図2のようになり,この状況を無理やり立式化すると,式(6)のようになります。

ここで,図2で示すようにx2を中心とする極めて小さい半径εの半円を複素数で表現すると,式(7)のようになります。

図2のように,半円上を左から右に進むと角度θはπ→0に変わります。よって,式(7)の赤枠部を使うと,増加量はπ-α2となります。
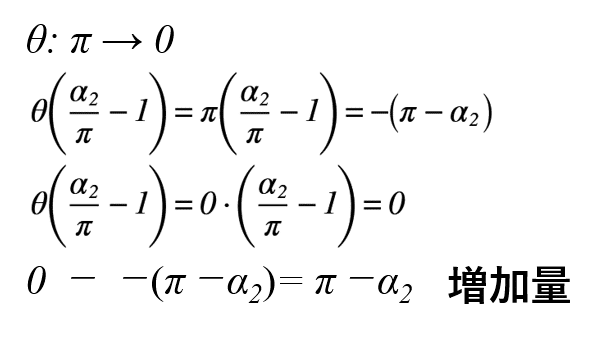
よって,π-α2は図1のζ平面の多角形の挑戦ζ2における外角に等しくなります。当然,直線はπとなるので,内角はα2と等しくなることもここで証明できます。
この結果,z平面の上半面の複素数は,ζ平面のn辺多角形になることを証明できたので,「ζ平面からz平面に変換するとz平面の上半面(x軸上,もしくはx軸の正の領域)に必ず存在する」ことを幾何学的に証明できました。(本当は,必要十分条件ではないという方もいるかと思いますが,今回は見逃しましょう。)
(4)まとめ
今回の記事のまとめを以下に示します。
① SCの定理は,エルヴィン・クリストッフェルとヘルマン・シュワルツの
2名の功績を称えたものである。
② ζ平面に示された内角α1,α2,α3,…,αnのn辺多角形ζ1,ζ2,
ζ3,…,ζnの内部は,シュワルツ・クリストッフェルの変換式を使う
ことで,z平面の上半面に変換される。
③ SCの定理を幾何学的な証明をするには,z平面の上半面からζ平面に変換
したときの外角および内角が等しいことで証明できる。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「シュワルツ・クリストフェルの定理(その2)」について,解説する予定です。
サポートをして頂けると大変助かります。何かの支援ができるかもと思われた人をは何卒よろしくお願いします!
