流体力学　渦に関する法則（その3）

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第３５回目は，前回の予告通り「渦に関する法則」について紹介していきます。

（１）渦の何を取り扱うのか？

　 では，「渦に関する法則」について，解説していく訳ですが，筆者以外は，「何をそんなに取り上げる必要があるの？」と思うはずです。そこで，「渦に関する法則」として取り上げる内容を以下に箇条書きで示します。そして，各項目で記事にする予定ですので，興味のある分野や関連項目で見たいなどでいいかと思います。

（ⅰ）渦管を取巻く閉曲線Cで循環Γが成立するのか。
（ⅱ）2次元平面から3次元曲面でも循環Γが成立するのか。
（ⅲ）2次元流れの渦度は時間経過によってどう変化するのか。
（ⅳ）閉曲線Cに沿う循環Γは時間経過でどう変化するのか。

　基本的には，渦と取り扱うときに必ず登場する循環Γがどのようなモデルでも成立するのかをメインに取り扱います。今回は，「（ⅲ）2次元流れの渦度は時間経過によってどう変化するのか。」について投稿していきます。

（２）2次元流れの渦度は時間経過によってどう変化するのか。

（２－１）数式による証明（準備編）

　今回は， 数式による証明をメインに考えていきます。結論から言えば，式（1）のように最終結果がなればよいのです。

　では，式（1）が何を示しているかというと，渦度が時間経過に伴って，ゼロになることを指しているのです。要するに，「渦度」がどの時間で見ても，ずっと「ゼロ」になるのです。
　この証明には，難しい数式が出てきますが，流体力学で普通のことです。流体という本来ならば，現象の予測が難しい学問になるほど数式はより煩雑になるようです（筆者の経験談）。

　それでは，証明するために必要な数式は，3つ存在します。
　1つ目は，ナビエ・ストークスの方程式（以下，N-S方程式）です。流体力学では，よく登場する（偏微分）方程式で，この方程式を解くことができれば，様々な流体現象を完全に解くことが出来るものです。すなわち，様々な流体現象を完全に把握することが出来ることと同義となります。但し，現在の数学では，解くことが出来ずに懸賞金まで掛けられているようですが，工学の世界では，この方程式が正しいかつ解くことが出来るものとして考えていきます。今回使用するN-S方程式は，非圧縮性流体かつ定常流れの場合を取り扱うオイラーの運動方程式と呼ぶ場合もあります。

　2つ目は，渦度の式です。本稿の主人公的な立ち位置なので，この式は必須です。この式が，ゼロとなれば「渦なし流れ」，ゼロ以外であれば「渦あり流れ」となります。詳しくは，以下の記事を参考にしてみて下さい。

　3つ目は，連続の式です。この式が「ゼロ」になると，x, y, z方向に流れる速度が一定値となります。要するに瞬間の速さで変動しているものが，平均化した平均の速さとして取り扱えるようになります。一度でも速度計測したことがある人は，平均の速さが使えることがどれだけありがたいか…。
　次項では，数式による証明をしていきます。

（２－２）数式による証明（実線編）

　では，本格的に証明してみましょう。ここで注意なのが，時間によって変化しない定常流れ，密度ρが変化しない非圧縮性流体を取り扱い，２次元流れとすることとします（よくわからない人は，とりあえず式を解くのを簡単にしているものと考えてください）。

　式（2）には，N-S方程式を使って，非圧縮性流体かつ定常流れとすると，非定常項，粘性項が省略されます。また，外力ポテンシャルUとしたときの2次元流れにおけるN-S方程式は，式（2），（3）のように表せます。

式（2）はｙについて偏微分，式（3）はxについて偏微分すると，式（4），（5）のように表せます。

　ここで，式（5）から式（４）を引き算すると，式（６）のように表せます。

　ここで，渦度の式を使ってx, yについてそれぞれ偏微分すると，式（７），（８）のように表せます。

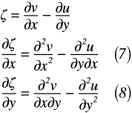
　さらに，連続の式を用いるため，式（９）のように表せると仮定したものを使います。

　それでは，式（７）～（９）を式（６）へ代入すると，式（１０）もしくは，式（１１）のように表せます。

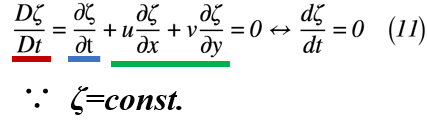
　したがって，2次元流れの渦度は時間経過によって変化しないことが分かりました。また，式（１１）の赤線部は，「実質加速度」と呼ばれているもので，非線形項とx, y, z軸の速度変動項をまとめたものになります。ちなみに，専門用語で非線形項（青線部）は「局所加速度」，x, y, z軸の速度変動項（緑線部）は「対流加速度」と呼ぶそうです。

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）渦に関する法則は，主に4つ取り上げる。今回は，（ⅱ）2次元平面から3次元曲面でも循環Γが成立するのか。
（２）2次元流れの渦度は時間経過とともに変化しないが，それはN-S方程式（もしくは，オイラーの運動方程式），渦度の式および連続の式の3つを用いる必要がある。
（３）実質加速度は，局所加速度と対流加速度を足したもので表せる。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，「渦に関する法則（その4）」について扱う予定です。