流体力学　流れ関数

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第４回目は，第２回目でネタにした「速度ポテンシャル」と切っても切り離せない「流れ関数」について，かいていきたいと思います。

（１）運動する流体の専門用語「流線」とは

　流れ関数の記事なのに，いきなり専門用語（テクニカルターム）の話をします。「そもそも，そんなもん知っとるわ！」という人は，次の項目へスルーしてください（決して，ブラウザバックを推奨してはいませんよ）。

　冗談はさておき，流体力学では，「流体要素」や「流体粒子」の話が頻繁に登場してします。

　ここでは，「流体粒子」の運動の様子について説明します。この専門用語を理解しないと意味も分からず，勉強することになり，非常にもったいないので，ここで紹介します。

　まず，図１に示すように，「流体粒子」の運動の様子を考えましょう。（普段の生活でのイメージは難しいですが，砂糖のような粒子状のものを川に流してみた状態を想像して頂ければよいのでは…）

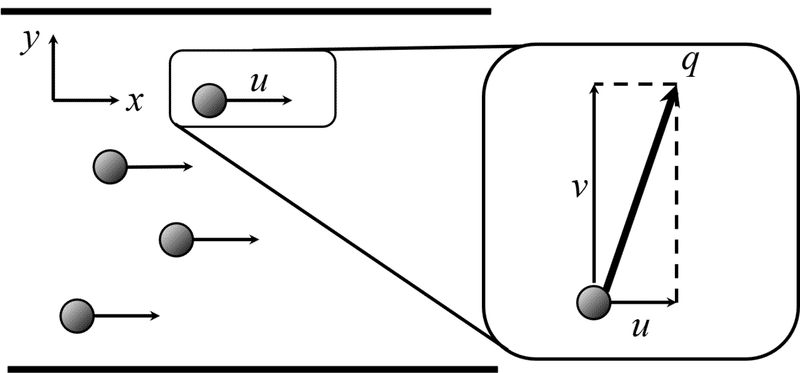
図1　流体粒子の運動の様子（u，v：直交座標x，yの速度成分，q：u，vの速度合成）

　流れのあるところに「流体粒子」があれば，その流体粒子は速度（厳密には，速度ベクトル）を持ちます。そして，とある速度を持った流体粒子は，適当なところに行くことは容易に想像がつくかと思います。

　今回は簡単に考えるため，図２に示すように，野球ボールを投げる場合をイメージしてみましょう（要するに，鉛直投げ上げ運動をする流体粒子を考える）。

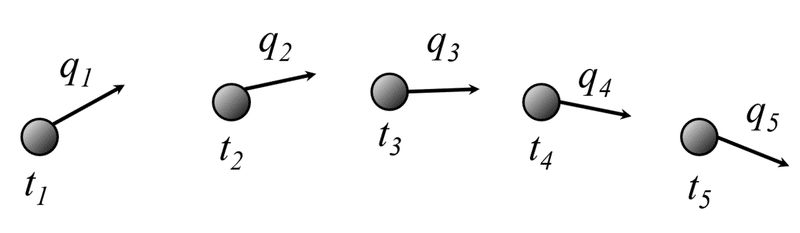
図２　各時間を止めて流体粒子の運動をとらえた様子

　では，図２の流体粒子を1つの線を書いてみた（数学的には，速度ベクトルの接線を繋げた）図３を考えましょう。

図３　流体粒子の速度ベクトルの接線をつないだ線

　図3に示した線を専門用語で「流線」と言います。つまり，「時間に対する流体粒子の運動の軌跡」を示したものなのです。
　
　なぜ，今回は「流線」を扱ったかというと，「流れ関数」で使うからです。ですが，流れ関数を扱うときには，何者かわからずに取り組み始めることが多いため（筆者がそうでしたので…），途中で，何だかわからないからとりあえず覚えてしまおうという発想をして，非常にもったいないのです。
　
　でも，ここでこんな疑問を持った人はすごいです！

「流線って，こんなきれいな曲線でかけるの？」

　答えは簡単なのです。この答えは，「定常流れ」だからです！定常流れの対義語として，「非定常流れ」がありますが，両者の流れの説明を箇条書きにしてみます。

・定常流れ：流れが時間的に変化しない状態（→一定の速度で流れている様子）
・非定常流れ：流れが時間的に変化する状態（→速度が変わる状況で流れている様子）

　なぜ，「非定常流れ」を図にせず，説明もあえてしなかったのでしょうか。

　答えは，「難しいすぎる」からです。というより教科書で学ぶレベルを超えているというか，今まさに，大学・高専の先生や公的機関で働く研究者が研究しているからです。
　定常流れで考えれば，時間変化を考えずに済むので，取扱いや数学的な記述もがかなり楽になります。
　
　ここからは，流線の数学的な記述を考えましょう。ここでも，２次元流れを考えると，直交座標x，yの速度成分をそれぞれu，vをとして，古典力学で使う微分形式でかくと，式（１）のように表せます。

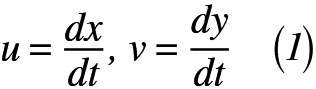
　では，直交座標ｘ，yの傾き（＝勾配）を考えると，式（２）で表せます。

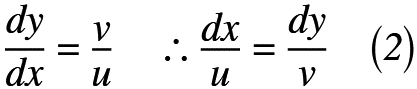
　式（２）が流線の式を呼ばれるもので，圧縮性・粘性を考慮しても同じ式が使えるという非常に万能な式なのです。では，流線から「流れ関数」の導出までしてみましょう。

（２）流線から流れ関数へ

　先ほどは，「流線」を取り扱いましたが，式（２）を使って「流れ関数」の式を導きましょう。流線の式をまず，式（３）のように書き換えましょう。

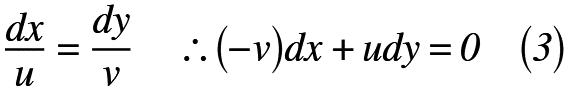
　速度ポテンシャルと同様に，任意の1点のｘ，ｙ方向の速度成分をそれぞれu，ｖとし，ｘ，ｙのある関数ψとしたときの全微分は，式（４）で表される。

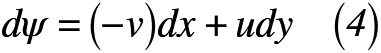
　　一方，関数ψの全微分は，式（５）で表される。

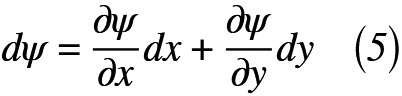
　式（４）と式（５）を比較すると，式（６）のように表される。

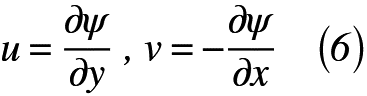
　ここで，関数ψの第2次偏導関数の関係は式（７）で表される。

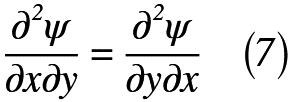
　よって，式（７）の関係を式（６）に代入すると，式（８）のように表される。

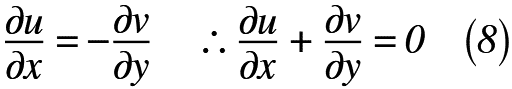
　式（８）満足するｘ，ｙの関数ψ(x, y)が必ず存在するとき，ψを「流れ関数」といいます。

　また，流れ関数ψは，速度ポテンシャルφと同様にスカラー量（方向を持たない，ただの大きさ）であり，流体の運動の軌跡を知ることができ，ψ＝const.（一定値）で表される線は流線となります。

　さらに，過去の記事でも取り上げた「渦流れと渦無し流れ」ですが，速度ポテンシャルψと同様に渦が存在しなくとも，「流れ関数ψは存在する」ことになります。

（３）流れ関数の物理的意味

　さて，流れ関数は「流線」と同じもののように使っていますが，その検証はしていません。ここでは，その証明をするため，図４に示すように，流体中に任意の点Ａ，Ｂを設定し，そのＡ，Ｂを結ぶ曲線の長さをdsとしたとき，左から右へ流れる流量Ｑを考えてみましょう。

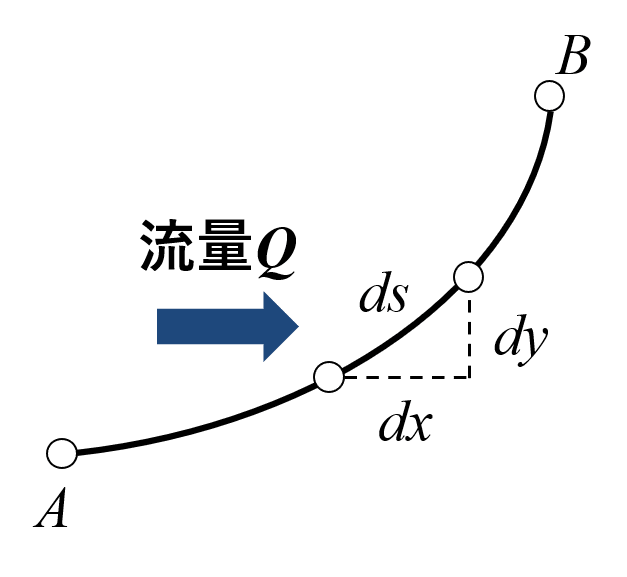
図４　曲線ABを流れる流量

　このとき，曲線ＡＢを横切る流量Ｑは，式（９）のように表される。

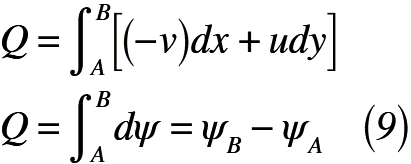
　これにより，曲線ＡＢを横切る流量Ｑは，Ａ，Ｂ点におけるψA，ψBだけが関係し，Ａ，Ｂを結ぶ経路にはまったく無関係であることが分かります。

　でも，少し流量について知っていると，式（９）までの経過に疑問を持ちませんか。

「本当にあってるの？」
「単位が違う気がするのだが？」

　ここで，疑問を完全に解決できるとは思いませんが，微分と積分の単位の変化について話したいと思います。古典力学では，必ず触れる話に位置，速度，加速度の話があります。図５に位置，速度，加速度の微分積分と単位について示します。

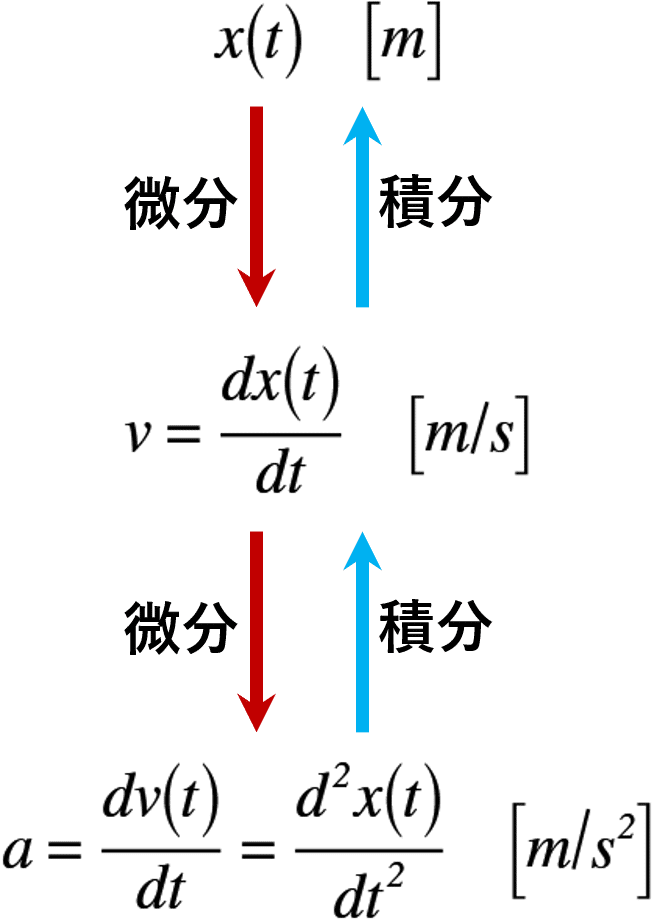
図５　位置，速度，加速度の微分積分と単位の関係について

　図5を見て頂くと，微分すればするほど「〇時間当たり」や「毎秒」の言葉が増えていきます。一方，積分をすればするほど「〇時間当たり」や「毎秒」の言葉が消え，「距離」だけが残っていきます（あくまで，時間について微分積分した場合の話ですが…）。

　流量の一般的に使用する単位は［m^3/s］（立方メートル毎秒）です。そして，今回扱った流れ関数の微分形dψの単位は［m^2/s］（平方メートル毎秒）なのです。図６に流量と流れ関数の微分積分と単位を示します。

図６　流量と流れ関数の微分積分と単位について

　今回は流れ関数の微分形dψは，距離について積分するわけですから，［m］（メートル）が追加されるので［m^2/s］から［m^3/s］となり，流量の単位と一致します。

　なんとなく納得できたでしょうか？

（４）流れ関数と流線の関係

　先ほどは，流線を横切る流量を考えたときの流れ関数を扱いました。しかし，流線を横切るような流ればかりではありません。時には，流れと同じ方向なときはどうなのでしょうか？

　図７に流体中に任意の点Ａ，Ｂ，Ｂ‘の流れ関数をそれぞれψA，ψB，ψB’としたときの曲線ＡＢ，曲線ＡＢＢ‘を通る流量Ｑ，Ｑ’として考えてましょう。

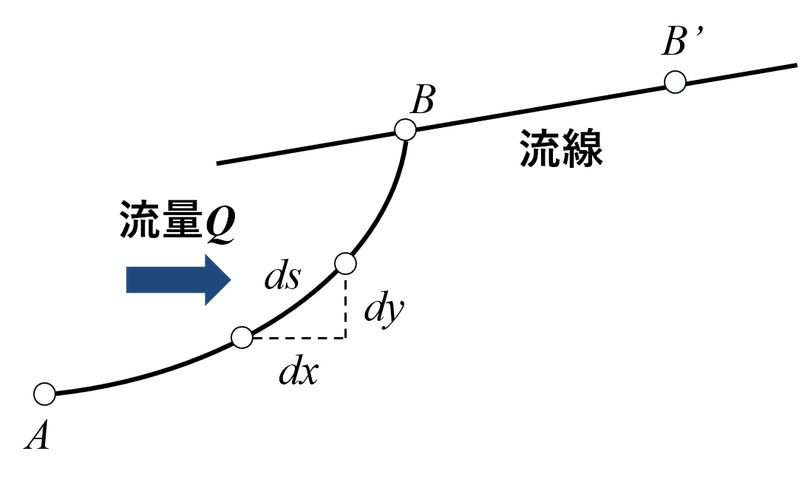
図７　曲線AB，曲線BB’を流れる流量

　これを数式化すると，式（１０）のように表される。

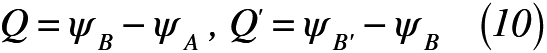
　ＢＢ‘は流線であることから，横切る流量はない。そこで，ＡＢを通る流量Qは，ＡＢＢ’を通る流量Q‘に等しくなるため，式（１１）が成立する。

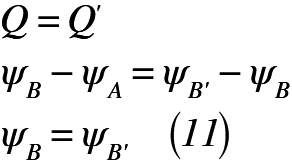
　したがって，ψ＝const.（一定値）の示す曲線は，どんな状況でも「流線」であることが分かりました！

（５）まとめ

　今回の記事のまとめを以下に示します。
（１）時間に対する流体粒子の運動の軌跡が「流線」である。
（２）流線の式から「流れ関数」を証明でき，流線と同様に流体の運動の軌跡を知ることができる。
（３）流量を横切っても，横切らなくても，ψ＝const.（一定値）の曲線は「流線」となる。

　以上です。最後まで閲覧頂きありがとうございました。