補足編　三角関数の無限乗数

　皆様おはこんばんちは。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　今回は，第42回目で解説した「渦の層と渦列」で使用した「三角関数の無限乗数」について紹介していきます。筆者自身は，あくまでも機械工学専攻なので，理学部の方々のような数学的に厳密な理論展開はせず，使うためのざっくりした説明であることを予めご了承ください。

（１）複素関数の無限乗積表示

　いきなりですが，ここでは大学・高専で履修することが多い「複素関数」の履修内容について，少し触れます。その後，複素関数の「表示方法」までの経路を紹介します。

　多くの複素関数の講義で取り扱うのは，「正則（せいそく）関数」（言い換えると，複素平面内で微分可能）であるかどうかです。正則関数の判定には，「コーシーの判定条件」が使われ，判定条件から「正則」かどうかを判別します。もし，正則である場合は，初等関数（べき関数，三角関数，指数・対数関数，逆関数など）がテイラー展開（もしくは，マクローリン展開）やローラン展開などの「級数展開」が可能になります。そして，この級数展開を使って，「留数解析」が可能です。おそらく，多くの大学・高専で取り扱うのは，ここまでではないでしょうか（筆者は高専時代，半期で留数解析までやりました）。
　しかし，正則条件が成立している場合，前述した級数展開の他に，複素関数の「表示」方法が存在します。今回取り扱う「無限乗数」は，式（１）のような複素関数の数列を各項の積で表示したものになります。

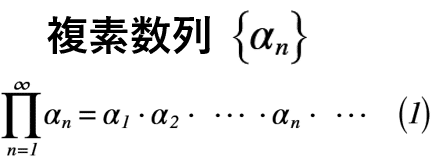
　これが「無限乗積」の一般式となります。数学の慣習？として，足し算の数列を「Σ」，掛け算の数列を「Π」と表すことが多いようです（筆者談）。また，多項式の形を取る場合は，式（２）のように表せます。

　ここまで，無限乗積の定義を説明しましたが，複素関数の一般式でこれが成立するかを考えます。
　複素関数f(z)が複素平面内で点a1，a2，…で1位の零点を持つ（ざっくり言い換えると，1次関数で，zが原点となるとき必ず複素関数がゼロになる）整関数f(0)≠0とします。上記の考え方を適用すると，複素関数f(z)が正則になる条件を満たすときに，複素関数f(z)は，「部分分数表示」の式（３）のように表せます。

　そして，部分分数表示が可能な場合は，f’(z) / f(z)のとき，複素関数f(z)が正則になる条件を満たすため，式（４）のように表せます。

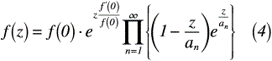
　この式（４）のことを「無限乗積表示（無限乗積展開，因数分解表示）」というそうです。では，この定理を使って，三角関数sin(πz/a)の無限乗積を証明していきましょう。

（２）三角関数sin(πz/a)の無限乗積（証明編）

　まず，条件を確認します。複素関数f(z)は，a1，a2，…，anより1位の零点をとすると，f’(z) / f(z)のとき，a1，a2，…，anより1位の極（言い換えると，1次関数の解）かつ留数が1となります。よって，この条件を使って，式（3）の「部分分数表示」は，式（５）のように書き換えが出来ます。

　ここで，式（５）をzについて積分すると，式（６）のように表せます。

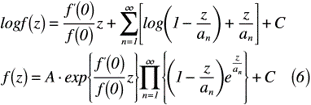
　つまり，式（６）の結果から，部分分数表示から無限乗積表示へ切り替えが出来ました。ここで，f(z)=sinz / zと置き，式（６）へ代入する前に必要なものを準備します。
　まず，留数を数えるため，z=0の場合を考えると，留数は以下に示すように「1」となります。

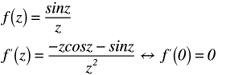
　次に，n位の極をz=0の場合で考えると，以下に示すように「１位の極」よなります。

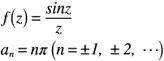
　では，これらの関係式を，式（６）へ代入すると，式（７）のように表せます。

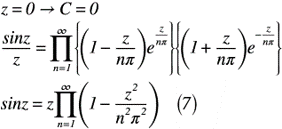
　最後に，z→（πz/a）とすると，式（８）のように表せます。

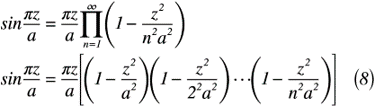
　この式（８）が「三角関数の無限乗積表示」です。複素関数では，級数展開をよく取り扱いますが，別の表示方法があることを利用した高等数学でした。
　ちなみに，cosやtanもありますが，筆者のモチベーションはあくまで機械工学で使う高等数学を解説することなので，今回は省きます。無限乗積表示については，多くの方々がブログ等で記事を書いている人も教科書もありますので，探してみて下さい。筆者が参考にした文献は，以下に示す通りです。

【参考文献】
（ⅰ）詳解物理応用数学演習，後藤憲一他２名，共立出版，初版p163，p168（1979）

（３）まとめ

今回の記事のまとめを以下に示します。
（１）複素関数では，級数展開以外に，別の表示方法が存在する。
（２）三角関数の無限乗積は，部分分数表示が成立することを前提に，無限乗積表示が可能となる。

　以上です。最後まで閲覧頂きありがとうございました。

　今回の解説内容は，「渦の層と渦列」についての補足です。渦列では，このような関数の表示が特殊なケースがあるようなので，どこかでまた使うかもしれません…。