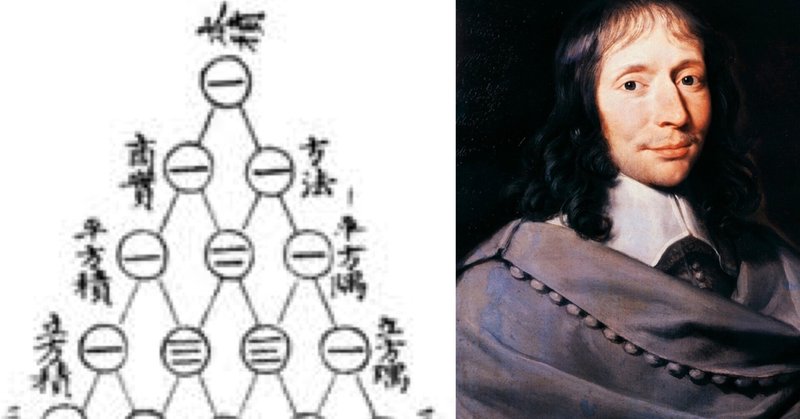
MT数学史#4 古代中国の記数法と先進性

バビロニアやエジプトと比べてあまり印象深くない中国数学文化ですが、そのレベルは贔屓目を差し引きエジプトとバビロニアに比べても世界最高峰でした。

古代バビロニアとエジプトでは中学数学くらいの算術・代数・幾何は扱われていることをみてきましたが、古代中国ではさらにかなりのレベルに達していました。

先ずは算術から。というかこれがすごい。次の表のように早くから十進換字法で、乗数的に表現していました。つまり僕らが漢数字を書くのと同じシステムです。

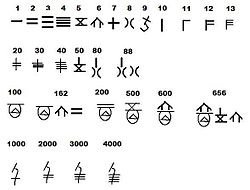
甲骨文化だけあってちょっとデザインがいいですね。

とはいえこれまた早い段階で、実用のための次のような算木表記が現れます。

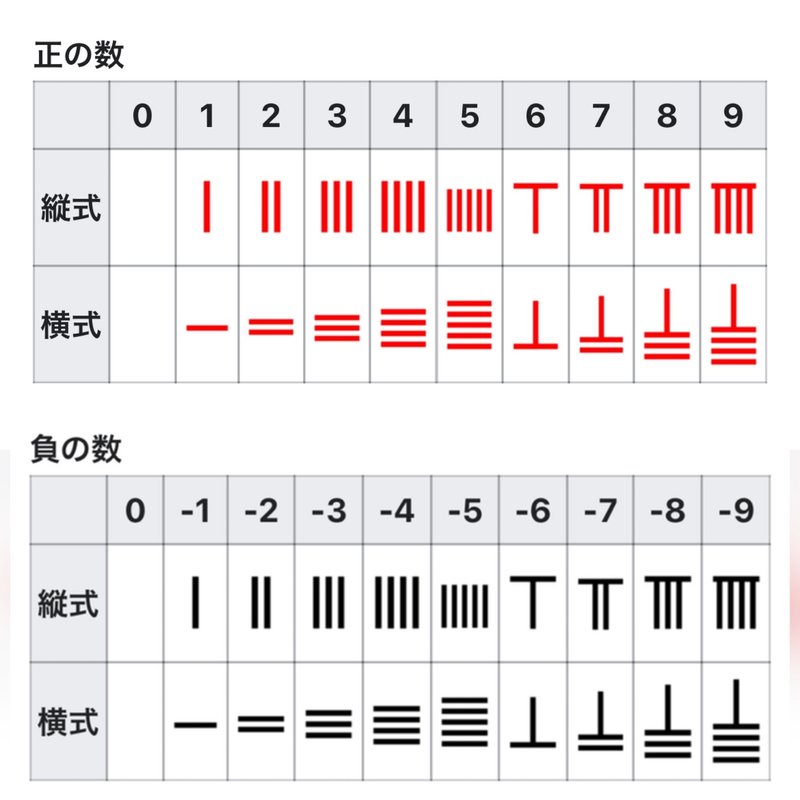
正負の黒赤が日本と入れ替わっているのが変なところ。もちろん順番でいえばこちらが変。

これは、次の表のように方眼紙のようなマス目の板に、一つのブロックがとある桁の数字を表すようにして使います。

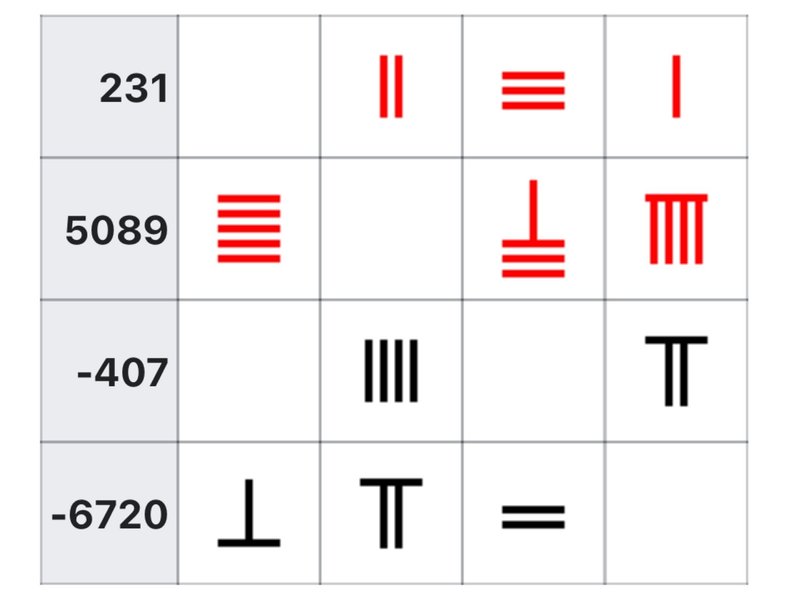
縦置きと横置きの違いはこの算板を使うときの都合で、一つおきに用いることで視認性と桁間違いによる計算ミスを防いでいたようです。すごい。

ゼロを表すのには空白を用いていますから、木の棒を使っているとはいえシステムはもう立派に十進位取り記数法ですね。しかし空を埋めるための記号はまだなのであと一歩足りないといえばそうかもしれませんが、そもそも算板の上では埋める一つようもないので何とも言い難いところです。

筆記用の漢数字一二三四五六七八九なども「九章算術」くらい早くから用いられていたとのことです。こちらは零が大切ですれけど。

算板と桁の意識から、十進小数計算も十分に機械化・高度化されていました。そのためか、分数はそんなに発展しなかったようです。必要は発明の母。

しかしそれをカバーしてあまりあるほど、古代においてさえ開平・開立、ニュートン法やホーナー法、行列表記や高次方程式の解法にまで及んでいるのは、西洋どころか中世アラビアにさえ先んじていたのではないかといわれています。その基礎的基盤は二項定理などの代数的知識でしたから、十分に「代数的事実」は知られていたようです。しかしここで鉤括弧をつけた理由は、あくまで出てくるものは数と算術であり、現代的な代数的観念や文字式では無いので注意しておきましょう。

なぜ開平・開立ほどの特殊な近似計算が必要であったか？それももちろん幾何学的要請でしょう。直角三角形の斜辺の長さや体積から一辺などを知るためには二乗根や三乗根が必要で、裏を返せばピタゴラスの定理などの事実は知られていたワケです。ちなみに漢語では鉤股弦定理などと呼びます。

幾何学的に代数を考えるのもお手のもので、平方根√xを求めるときに、与えられた数を正方形の面積xとみなしてその一辺を求めようとしています。その際、まずは整数の長さで内側に目一杯入るギリギリの正方形a^2をあたえ、残りの部分を2ab+b^2として、ときにはこれを正方形に直して同じ操作に帰着させたり、b^2は十分小さいとみなして無視し、x=a^2+2abからとりあえず近似でbを求め満足したりしています。
前者はアルゴリズム的思考、後者は1/2乗の二項定理の第一近似に相当します。

これを立体で同じようにすることで三乗根の近似などもしていますからカルダノにも匹敵しています、代数と算術という問題意識の差こそあれど。

算術と代数と幾何、そしてその実用まで射程に含め、有機的に理解されていたのは驚きです。もちろん非実用的問題まで扱っているからこそこれぐらいの余裕のあることができたようで、バビロニアにしろエジプトにしろ中国にしろ問題集とその解法という形で文献が残っていることが多いです。エリート養成はいつの時代も重要のようで、今でも問題集問題集いっとりますもんねぇ。

ちなみにインダスは詩で残していることがおおく、よく歌っとります。

というわけで、

古代中国は当時の他文明に比しても高度に数学が発達していたようです。焚書坑儒等の政争や災禍をくぐり抜け、そういうものが人から人に伝えられてきたかと思うと素晴らしいですね。

よければフォローとサポートよろしくお願いします。

MT

おまけ

少しばかり日本の数学の片鱗を、ここにしか書けないので書いておきます。

古代日本にも古代中国から仏教や五経博士と共に文献に紛れ込んで数学は入ってきたようで、厩戸皇子は算術と幾何と呪術に長じていたようです。万葉集などにも九九で洒落た読みをさせた歌などがあるということは、読み書きができるくらいの上流階級には万葉の頃から九九は浸透していたようです。獅子(しし)を十六とかいたり、憎く(にくく)を二八十一とかいたり、調べてみると面白いですよ。