
高校数学をプログラミングで解く(数学B編)「3-5 いろいろな数列の和」
マガジンリスト > 数学B編 3.数列 > 3-5 いろいろな数列の和
はじめに
今回は、数学Bで学ぶ「いろいろな数列の和」について、群数列の問題や自然数の並べ方に関する問題を解くためのプログラムを作成します。
群数列の問題
まず、次のような数列の問題を考えてみます。
問題1
自然数の列を次のような群に分けるとき
$${ \{1\}, \{2,3\}, \{4,5,6\}, \{7,8,9,10\}, \{11, \cdots \}, \cdots }$$
(1) 第$${n}$$群の$${m}$$番目の数を与える関数を作成して、第$${10}$$群の$${10}$$番目の数の値をコンソールに出力せよ。
(ヒント:まず第$${n}$$群の最初の数を求める)
(2) 第$${n}$$群の数の和を求める関数を作成して、第$${10}$$群の数の和の値をコンソールに出力せよ。
解析的な解答
この問題1は数学の問題として一般項を求めることができます。
(1)については、第$${n}$$群の$${m}$$番目の数を$${a_{n,m}}$$とすると、
$$
a_{n,m} = \frac{1}{2} n(n-1)+m \ \ \ \ (n=1,2,\cdots, \ \ 1 \leq m \leq n )
$$
と表すことができます。ヒントに書いたように、これを求めるため各群の最初の数の数列が$${1, 2, 4, 7,\cdots}$$となることに注目すると、その階差数列が$${1,2,3,\cdots}$$、すなわち、初項$${1}$$、公差$${1}$$の等差数列($${b_n}$$とします)となっています。そのため、第$${n}$$群の最初の数$${a_{n,1}}$$は
$$
a_{n,1} = a_{1,1}+\sum_{k=1}^{n-1} b_n = \frac{1}{2} n(n-1)+1 \ \ \ \ (n=1,2,\cdots)
$$
となります。$${a_{n,m}}$$はこの$${a_{n,1}}$$に$${m-1}$$を加えたものであることに気付けば、上記の$${a_{n,m}}$$を求めることができます。
(2)は、第$${n}$$群の数の和を$${S_n}$$とすると、
$$
S_n = \sum_{m=1}^n a_{n,m} = \frac{1}{2}n(n^2+1)
$$
のように計算することができます。
プログラムの作成
では、問題1の解を求めるプログラムを作成します。
// 群数列の問題
void setup(){
int n = 10; // 第n群
int m = 10; // m番目
// (1) 第n群のm番目の数
println("(1)第"+n+"群の"+m+"番目の数:", group_progression(n,m));
// (2) 第n群の数の和
println("(2)第"+n+"群の数の和:", sum_group_progression(n));
}
// 初項a,公差dの等差数列の第n項を求める関数(一般項)
float calc_arithmetical_progression(
float a, // 初項
float d, // 公差
int n // 第n項
){
return a + (n-1)*d;
}
// 第n群のm番目の項の値を返す関数
float group_progression(
int n, // 第n群
int m // 第n群のm番目の項
){
float a_nm = 1.0; // 初項a_11で初期化
// 各n群の1番目の項の階差数列が初項1,公差1の等差数列になることを利用
for(int k=1; k<n; k++){
a_nm += calc_arithmetical_progression(1.0,1.0, k);
}
a_nm += m-1.0;
return a_nm;
}
// 第n群の数の和を返す関数
float sum_group_progression(
int n // 第n群
){
float S_n = 0.0;
for(int k=1; k<=n; k++){
S_n += group_progression(n,k);
}
return S_n;
}ソースコード1 問題1のプログラム
今回は、第$${n}$$群の$${m}$$番目の数$${a_{n,m}}$$を関数 group_progression として作成しました。group_progression 関数は引数として、
n:第$${n}$$群 int型
m:第$${n}$$群の$${m}$$番目 int型
を取ります。返り値は$${a_{n,m}}$$の値を返します。なお、group_progression 関数の処理として、各群の最初の数の数列の階差数列が初項$${1}$$、公差$${1}$$の等差数列となっていることを利用しています。
また、第$${n}$$群の数の和$${S_n}$$を関数 sum_group_progression として作成しました。sum_group_progression 関数は引数として、
n:第$${n}$$群 int型
を取ります。返り値は$${S_n}$$の値を返します。group_progression 関数の処理は、group_progression 関数を用いて第$${n}$$群の$${n}$$個の項をすべて足し上げて計算するようにしています。
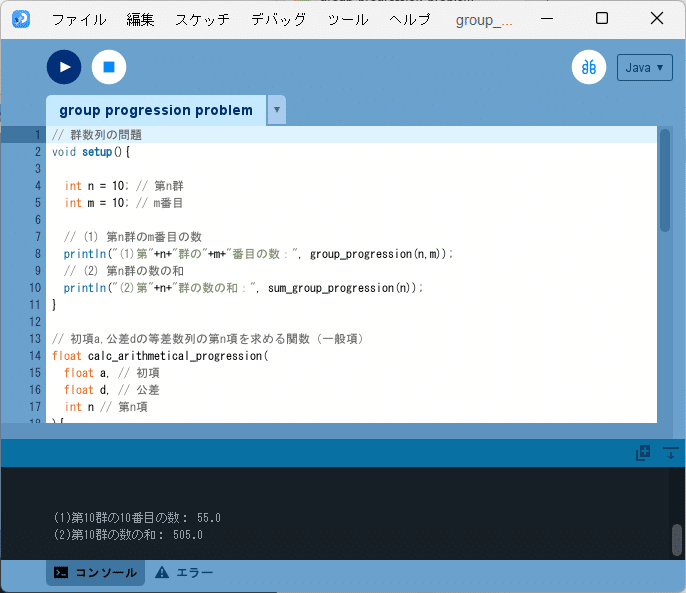
ソースコード1を、Processingの開発環境ウィンドウを開いて(スケッチ名を「group_progression_problem」としています)、テキストエディタ部分に書いて実行すると、開発環境ウィンドウのコンソール部分に
(1)第10群の10番目の数: 55.0
(2)第10群の数の和: 505.0
と出力されます(図1)。
自然数の並べ方に関する問題
次に、以下のような数列の問題を考えてみます。
問題2
図2のように、自然数$${1,2,3,4, \cdots }$$が並んでいる。
上から$${n}$$行目、左から$${m}$$列目の数を与える関数を作成して、上から$${10}$$行目、左から$${10}$$列目の数の値をコンソールに出力せよ。
(ヒント:まず1行目の数列と1列目の数列の一般項を求める)

解析的な解答
上から$${n}$$行目、左から$${m}$$列目の数を$${a_{n,m}}$$とします。ヒントに基づいて、まず上から$${1}$$行目、左から$${m}$$列目の数$${a_{1,m}}$$を求めてみます。上から$${1}$$行目の数列が$${1, 2, 5, 10,\cdots}$$となることに注目すると、その階差数列が$${1,3,5,\cdots}$$と奇数の列となっているので、$${a_{1,m}}$$は
$$
a_{1,m} = (m-1)^2+1 \ \ \ \ (m=1,2,\cdots)
$$
となります。一方、上から$${n}$$行目、左から$${1}$$列目の数$${a_{n,1}}$$を求めてみます。左から$${m}$$列目の数列が$${1, 4, 9, 16,\cdots}$$となることに注目すると、$${a_{n,1}}$$は
$$
a_{n,1} = n^2 \ \ \ \ (n=1,2,\cdots)
$$
となります。これらの結果と図2とを見比べてみると、左から$${m}$$列目の数$${a_{n,m}}$$は、$${n \leq m}$$のとき
$$
a_{n,m} = n+(m-1)^2
$$
となり、$${n>m}$$のとき、
$$
a_{n,m} = n^2-m+1
$$
となります。
プログラムの作成
では、問題1の解を求めるプログラムを作成します。
// 自然数の並べ方に関する数列の問題
void setup(){
int n = 10; // 上からn行目
int m = 10; // 左からm列目
// 上からn行目、左からm列目の数
println("上から"+n+"行目、左から"+m+"列目の数:", matrix_progression(n,m));
}
// 上からn行目、左からm列目の数を返す関数
float matrix_progression(
int n, // 上からn行目
int m // 左からm列目
){
float num = 0.0;
if(n <= m){
num = n+(m-1.0)*(m-1.0);
} else {
num = n*n-m+1.0;
}
return num;
}ソースコード1 問題2のプログラム
今回は、上から$${n}$$行目、左から$${m}$$列目の数$${a_{n,m}}$$を関数 matrix_progression として作成しました。matrix_progression 関数は引数として、
n:上から$${n}$$行目 int型
m:左から$${m}$$列目 int型
を取ります。返り値は$${a_{n,m}}$$の値を返しますが、上記で記載した通り、n <= m のときとそうでないときで場合分けが必要になります。
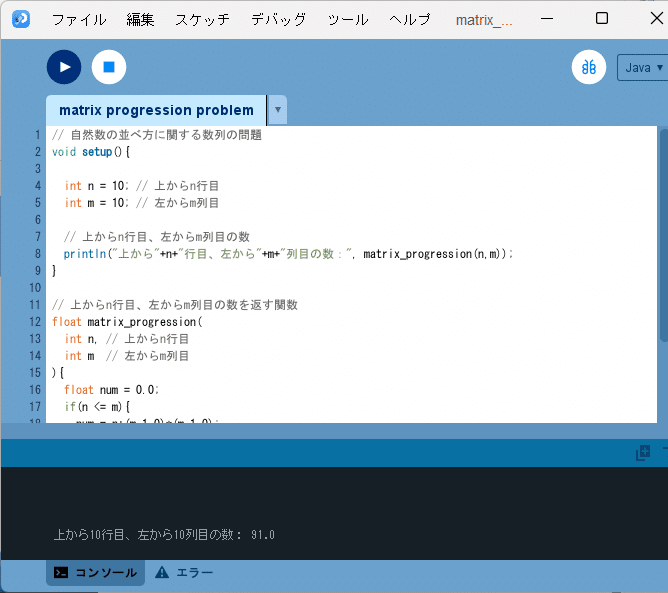
ソースコード2を、Processingの開発環境ウィンドウを開いて(スケッチ名を「matrix_progression_problem」としています)、テキストエディタ部分に書いて実行すると、開発環境ウィンドウのコンソール部分に
上から10行目、左から10列目の数: 91.0
と出力されます(図3)。
まとめ
今回は、数学Bで学ぶ「いろいろな数列の和」について、群数列の問題や自然数の並べ方に関する問題を解くためのプログラムを作成しました。
いずれの問題でも問題を解析的に解いてそれをそのままプログラミングしましたが、解析的に解く部分が大変で、プログラム作成は比較的簡単に感じたのではないでしょうか。
実際のシステム構築などでもプログラム作成に必要なアルゴリズム設計が重要で大変な作業になり、このアルゴリズム設計は数学(特に高校で学ぶ数学)を利用することが多いです。そのため、高校数学をプログラミングして解いておく訓練をしておくことは重要だと考えています。是非、ここで紹介している記事を読んでいって力をつけていってください。
参考文献
改訂版 教科書傍用 スタンダード 数学B(数研出版、ISBN9784410209468)
