高校数学をプログラミングで解く（数学A編）「3-2 最大公約数と最小公倍数」

MK's papa

2023年9月16日 06:22

マガジンリスト　＞　数学A編 3.整数の性質　＞　3-2 最大公約数と最小公倍数

はじめに

今回は、数学Aで学ぶ「最大公約数と最小公倍数」について、2つの整数$${M}$$と$${N}$$に対する最大公約数と最小公倍数を求めるプログラムを作成します。

整数MとNの最大公約数を求める

まず、整数$${M}$$と$${N}$$の最大公約数を求めるプログラムを作成していきます。

整数MとNの最大公約数の求め方

まず、整数$${M}$$と$${N}$$をそれぞれ素因数分解します。素数$${p}$$までの素数を用いて分解できるとすると、

$$
M=2^{m_2} \cdot 3^{m_3} \cdot 5^{m_5} \cdot \cdots \cdot p^{m_p} \\
N=2^{n_2} \cdot 3^{n_3} \cdot 5^{n_5} \cdot \cdots \cdot p^{n_p}
$$

と表わすことができます。このとき、

$${m_2}$$と$${n_2}$$のうち、小さい方を$${l_2}$$とする
$${m_3}$$と$${n_3}$$のうち、小さい方を$${l_3}$$とする
$${m_5}$$と$${n_5}$$のうち、小さい方を$${l_5}$$とする
・・・
$${m_p}$$と$${n_p}$$のうち、小さい方を$${l_p}$$とする

と各冪の指数の小さい方を選んでいき、それら$${l_2, l_3, l_5, \cdots , l_p}$$を指数とする整数を求めると、それが整数$${M}$$と$${N}$$の最大公約数$${\mathrm{GCD}}$$となります。

$$
\mathrm{GCD} = 2^{l_2} \cdot 3^{l_3} \cdot 5^{l_5} \cdot \cdots \cdot p^{l_p}
$$

整数MとNの最大公約数を求めるプログラム

$${M=12}$$と$${N=30}$$の最大公約数を求め、コンソールに出力するプログラムを作成します。

// 整数MとNの最大公約数を求める
void setup(){
  // 整数M,N（ただし、2以上の整数）
  int M, N;
  M = 12;
  N = 30;
  
  // MとNのうち、大きい方を整数N_gtとし、N_gt以下の素数を求める
  int N_gt;
  if( M > N ){
    N_gt = M;
  } else {
    N_gt = N;
  }  
  // N_gt以下の素数を求める
  ArrayList<Integer> prime_numbers = getPrimeFactors(N_gt);
  
  // M, Nをそれぞれ素因数分解する
  ArrayList<Integer> exponents_M = primefactorization(M, prime_numbers);
  ArrayList<Integer> exponents_N = primefactorization(N, prime_numbers);

  // MとNの最大公約数を求める
  float GCD = 1.0; // 最大公約数
  int exponents_GCD; // 最大公約数を素因数分解した時のi番目の冪の指数
  for(int i=0; i<prime_numbers.size(); i++){
    if( exponents_M.get(i) < exponents_N.get(i)){
      exponents_GCD = exponents_M.get(i);
    } else {
      exponents_GCD = exponents_N.get(i);
    }
    GCD = GCD * pow(prime_numbers.get(i), exponents_GCD);
  }
  println(GCD);
}

ソースコード1　整数$${M}$$と$${N}$$の最大公約数を求めるプログラム

// N以下の素数を求める関数
ArrayList<Integer> getPrimeFactors(
  int N // 2以上の自然数
){
  // int型の可変配列を準備する
  ArrayList<Integer> prime_numbers = new ArrayList<Integer>();
  // 最初の素数2を可変配列に追加
  prime_numbers.add(2);
  
  int pn; // 素数を代入する変数
  boolean pn_flag; // 素数かどうかのフラグ
  // 3以上N以下の奇数について素数であるかを確認する
  for(int i=3; i<=N; i+=2){
    pn_flag = true;
    for(int j=0; j<prime_numbers.size(); j++){
      pn = prime_numbers.get(j); // j番目の素数を取り出す
      if( i%pn == 0 ){ // i未満の素数で割り切れたらiは素数でない
        pn_flag = false;
        break;
      }
    }
    if(pn_flag){
      prime_numbers.add(i); // iが素数と判定された場合、可変配列に追加
    }
  }

  return prime_numbers;
}

ソースコード2　自然数$${N}$$以下の素数を求める関数

// 素因数分解を行う関数
ArrayList<Integer> primefactorization(
  int N, // 素因数分解対象の自然数
  ArrayList<Integer> prime_numbers // 素数
){
  // 素因数分解したときの各冪に対する指数
  ArrayList<Integer> exponents = new ArrayList<Integer>();
  
  int quotient = N; // 素数で割ったときの商
  int pn;
  boolean divisible_flag; // 割り切れたかどうかを判定するフラグ
  int exponent_count;
  for(int i=0; i<prime_numbers.size(); i++){
    pn = prime_numbers.get(i); // i番目の素数を取り出す
    divisible_flag = true;
    exponent_count = 0;
    while(divisible_flag){
      if( quotient % pn == 0 ){ // 商が素数pnで割り切れた場合
        quotient = quotient / pn; // 商を更新する
        exponent_count++; // pnに対する指数の値を1増やす 
      } else { // 素数pnがNの素因数ではない、またはpnがNの素因数としてすべて算出された場合
        divisible_flag = false; 
      }
    }
    exponents.add(exponent_count);
  }

  return exponents;
}

ソースコード 3　整数$${N}$$を素因数分解する関数

ソースコード1、ソースコード2及びソースコード3を、Processingの開発環境ウィンドウを開いて（スケッチ名を「greatest_common_divisor」としています）、テキストエディタ部分に並べて書いて実行すると、図1のように、コンソールに整数$${M}$$と$${N}$$の最大公約数を出力します。今回は、$${12}$$と$${30}$$の最大公約数である「6.0」が出力されています。

整数$${M}$$と$${N}$$の値を変えてみて、正しい最大公約数が出力されるか試してみてください。

以下、プログラムに関してポイントを解説しておきます。

自然数N以下の素数を求める関数

最大公約数を求める際に、整数$${M}$$と$${N}$$をそれぞれ素因数分解しますが、その前に素因数分解を行うために必要な素数を求めておきます。これらの素数を求める方法とそのプログラムについては記事『高校数学をプログラミングで解く（数学A編）「3-1 約数と倍数」』で紹介しています。

今回はそのプログラムを関数化して利用しています（ソースコード2参照）。関数化については、記事『高校数学をプログラミングで解く（数学A編）「1-7 反復試行の確率」』の『プログラムの解説2「組合せの総数を計算する関数」』の節で紹介していますので、詳細はそちらをご覧ください。ここでは、その解説に沿って以下の手順で自然数$${N}$$以下の素数を求める関数を作成しています。
1. 関数名は「素数」（英語表記「Prime Factor」）を求めるという意味で「getPrimeFactors」とします。また、返り値は求めた素数を格納した可変配列となるので、関数のデータ型はArrayList<Integer>とします。
2. 関数の引数は、自然数$${N}$$（int型）を与えます。
3. 処理は記事『高校数学をプログラミングで解く（数学A編）「3-1 約数と倍数」』で紹介した素数を求める方法をベースにして記述します。返り値は求めた素数を格納した可変配列となります。

このように作成したgetPrimeFactors関数をメインのプログラム内で呼び出しています。（ソースコード1の

ArrayList<Integer> prime_numbers = getPrimeFactors(N_gt);

の部分）。なお、整数$${M}$$と$${N}$$のうち大きい方の値以下の素数を求めるようにしています。

整数Nを素因数分解する関数

最大公約数を求める際に、整数$${M}$$と$${N}$$をそれぞれ素因数分解します。素因数分解についても素因数分解する方法とそのプログラムを『高校数学をプログラミングで解く（数学A編）「3-1 約数と倍数」』で紹介しています。

素因数分解についてもそのプログラムを関数化していますが、今回は素因数分解した結果の各冪の指数を可変配列に保存して返り値として返すようにしています（ソースコード3参照）。
1. 関数名は「素因数分解」（英語表記「Prime Factorization」）をそのまま利用して「primefactorization」としています。また、返り値は素因数分解した結果の各冪の指数を保存した可変配列となるので、関数のデータ型はArrayList<Integer>とします。
2. 関数の引数は、素因数分解の対象となる自然数$${N}$$（int型）とgetPrimeFactors関数を用いて得られた自然数$${N}$$以下の素数（ArrayList<Integer>型）を与えます。
3. 処理は記事『高校数学をプログラミングで解く（数学A編）「3-1 約数と倍数」』で紹介した素因数分解を行う方法をベースにして記述します。返り値は素因数分解した結果の各冪の指数を保存した可変配列となります。

このprimefactorization関数をメインのプログラム内で整数$${M}$$と$${N}$$のそれぞれに適用して素因数分解した結果の各冪の指数を可変配列に保存するようにしています（ソースコード1の

ArrayList<Integer> exponents_M = primefactorization(M, prime_numbers);

と

ArrayList<Integer> exponents_N = primefactorization(N, prime_numbers);

の部分）。

整数MとNの最小公倍数を求める

次に、整数$${M}$$と$${N}$$の最小公倍数を求めるプログラムを作成していきます。

整数MとNの最小公倍数の求め方

最大公約数のときと同様に、整数$${M}$$と$${N}$$をそれぞれ素因数分解します。

$$
M=2^{m_2} \cdot 3^{m_3} \cdot 5^{m_5} \cdot \cdots \cdot p^{m_p} \\
N=2^{n_2} \cdot 3^{n_3} \cdot 5^{n_5} \cdot \cdots \cdot p^{n_p}
$$

このとき、

$${m_2}$$と$${n_2}$$のうち、大きい方を$${l_2}$$とする
$${m_3}$$と$${n_3}$$のうち、大きい方を$${l_3}$$とする
$${m_5}$$と$${n_5}$$のうち、大きい方を$${l_5}$$とする
・・・
$${m_p}$$と$${n_p}$$のうち、大きい方を$${l_p}$$とする

と各冪の指数の大きい方を選んでいき、それら$${l_2, l_3, l_5, \cdots , l_p}$$を指数とする整数を求めると、それが整数$${M}$$と$${N}$$の最小公倍数$${\mathrm{LCM}}$$となります。

$$
\mathrm{LCM} = 2^{l_2} \cdot 3^{l_3} \cdot 5^{l_5} \cdot \cdots \cdot p^{l_p}
$$

整数MとNの最小公倍数を求めるプログラム

$${M=12}$$と$${N=30}$$の最小公倍数を求め、コンソールに出力するプログラムを作成します。

// 整数MとNの最小公倍数を求める
void setup(){
  // 整数M,N（ただし、2以上の整数）
  int M, N;
  M = 12;
  N = 30;
  
  // MとNのうち、大きい方を整数Nとし、N以下の素数を求める
  int N_gt;
  if( M > N ){
    N_gt = M;
  } else {
    N_gt = N;
  }
  // N_gt以下の素数を求める
  ArrayList<Integer> prime_numbers = getPrimeFactors(N_gt);

  // M, Nをそれぞれ素因数分解する
  ArrayList<Integer> exponents_M = primefactorization(M, prime_numbers);
  ArrayList<Integer> exponents_N = primefactorization(N, prime_numbers);

  // MとNの最小公倍数を求める
  float LCM = 1.0; // 最小公倍数
  int powers_LCM; // 最小公倍数を素因数分解した時のi番目の冪の指数
  for(int i=0; i<prime_numbers.size(); i++){
    if( exponents_M.get(i) < exponents_N.get(i)){
      powers_LCM = exponents_N.get(i);
    } else {
      powers_LCM = exponents_M.get(i);
    }
    LCM = LCM * pow(prime_numbers.get(i), powers_LCM);
  }
  println(LCM);
}

ソースコード4　整数$${M}$$と$${N}$$の最小公倍数を求めるプログラム

なお、自然数$${N}$$以下の素数を求める関数や整数$${N}$$を素因数分解する関数は、最大公約数を求めたときと同じもの（ソースコード2, ソースコード3）を利用します。

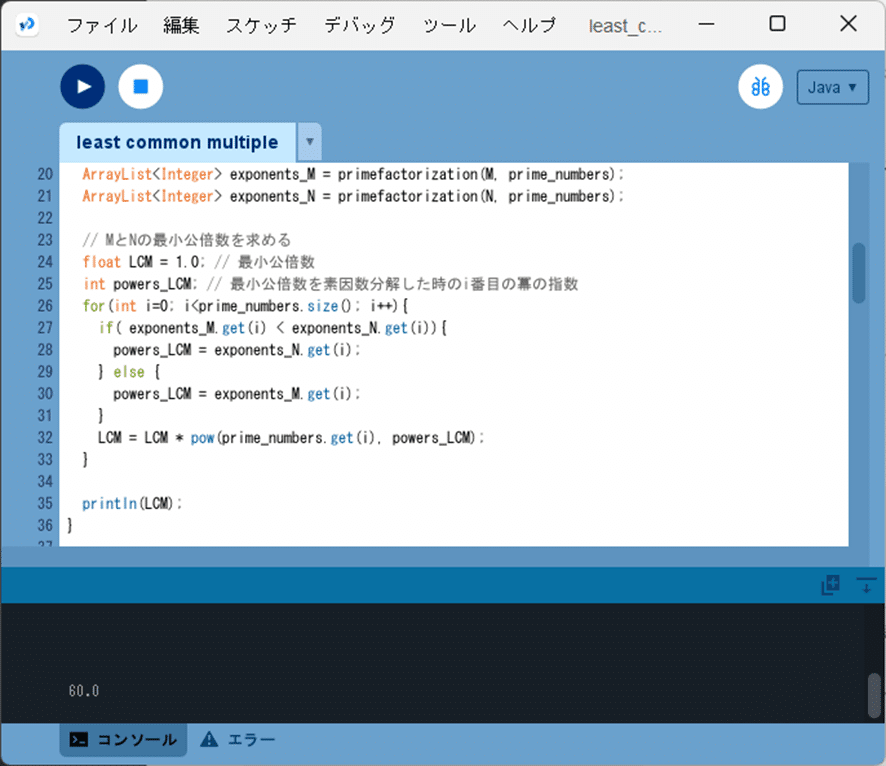
ソースコード4、ソースコード2及びソースコード3を、Processingの開発環境ウィンドウを開いて（スケッチ名を「least_common_multiple」としています）、テキストエディタ部分に書いて実行すると、図2のように、コンソールに整数$${M}$$と$${N}$$の最小公倍数を出力します。今回は、$${12}$$と$${30}$$の最小公倍数である「60.0」が出力されています。

まとめ

今回は、数学Aで学ぶ「最大公約数と最小公倍数」について、2つの整数$${M}$$と$${N}$$に対する最大公約数と最小公倍数を求めるプログラムを作成してみました。その中で、自然数$${N}$$以下の素数を求める部分や整数$${N}$$を素因数分解する部分は最大公約数と最小公倍数を求める、いずれのプログラムでも共通して行わなければならない処理ですので、関数化することで再利用できるようにしました。

今回作成したプログラムは、2つの整数$${M}$$と$${N}$$が互いに素であることを判定するプログラムを作成することに応用できます。2つの整数$${M}$$と$${N}$$が互いに素であるならば整数$${M}$$と$${N}$$の最大公約数が1になることを利用すれば簡単です。ぜひ一度作成してみてください。

また、今回は２つの整数を扱いましたが、３つ以上の整数に対する最大公約数や最小公倍数を求めるプログラムも作成することができます。こちらも一度チャレンジしてみてください。

参考文献

改訂版教科書傍用スタンダード数学A（数研出版、ISBN9784410209277）

この記事が気に入ったらサポートをしてみませんか？