
高校数学をプログラミングで解く(数学II編)「5-4 最大値・最小値」
マガジンリスト > 数学Ⅱ編 5.微分法と積分法 > 5-4 最大値・最小値
はじめに
今回は、数学IIで学ぶ「関数の最大値・最小値」について、特に3次関数に対する最大値・最小値を求め、3次関数のグラフに最大値・最小値を取る点をプロットするプログラムを作成します。
関数の最大値・最小値
まず、関数の最大値・最小値について解説しておきます。
関数の最大値・最小値
区間$${l \leq x \leq r}$$における$${f(x)}$$の最大値・最小値は、この区間での$${f(x)}$$の極値$${f(x_1), f(x_2)}$$と、区間の両端における値$${f(l), f(r)}$$とを比べて求める。

関数の最大値・最小値を求める
今回は、特に3次関数の最大値・最小値を求めるプログラムを作成します。
問題
次の関数の最大値と最小値を求めよ。
(1) $${y=x^3-27x}$$ ($${-4 \leq x \leq 4}$$)
(2) $${y=x^3-x^2}$$ ($${-1 \leq x \leq 1}$$)
(3) $${y=x^3-6x^2+9x}$$ ($${0 < x < 4}$$)
(4) $${y=x^3-\frac{7}{2}x^2 + 2x}$$ ($${-\frac{1}{2} < x < 3}$$)
アルゴリズム設計
関数の最大値・最小値の求め方は、上記で解説した通りですが、もう少し具体化して処理の流れをまとめます。
極値について
記事『高校数学をプログラミングで解く(数学II編)「5-3 関数の値の変化」』で扱った問題と同様に、今回の問題は3次関数に特化しているので、そのことを利用して極値を求めます。つまり、3次関数
$$
y=f(x) = ax^3+bx^2+cx+d \ \ (a \neq 0)
$$
の導関数は2次関数
$$
f'(x) = 3ax^2 + 2bx +c
$$
になりますので、2次方程式$${f'(x)=0}$$を解の公式を用いて、2つの実数解$${x_1, x_2}$$を求めることができれば、それら$${x_1, x_2}$$の位置に極値があることがわかります。なお、今回はこれらの極値が極大値であるか、極小値であるかは判定せずに最大値か最小値であるかを直接確認します。
処理の流れ
では、処理の流れについてまとめます。
① 最大値、最小値を格納する変数$${\mathrm{max}, \mathrm{min} }$$とそれらの位置$${x_{\mathrm{max}}, x_{\mathrm{min}}}$$を、区間の左端$${l}$$での3次関数の値$${f(l)}$$で初期化します。
$$
\mathrm{max} = f(l),
\mathrm{min} = f(l),
x_{\mathrm{max}} = l,
x_{\mathrm{min}} = l
$$
② 2次方程式$${f'(x)=0}$$が2つの実数解をもつか、つまり極値をもつかを確かめます。これは判別式
$$
D = (2b)\cdot(2b) -4\cdot (3a) \cdot c
$$
が正の値をもつかを調べることで判別できます。
③ 極値を持つ場合、それらの極値が最大値あるいは最小値になる可能性がありますので、それを確かめながら、$${\mathrm{max}, \mathrm{min} }$$を更新していきます。
極値の位置$${x_1, x_2}$$は、2次方程式$${f'(x)=0}$$を解の公式を用いて、
$$
x_1 = \frac{-(2b) - \sqrt{D}}{2\cdot (3a)}, \ x_2 = \frac{-(2b) + \sqrt{D}}{2\cdot (3a)}
$$
と計算することができます。計算した結果、極値の位置$${x_1, x_2}$$が$${l \leq x \leq r}$$の区間に含まれているかを確認しておきます。
区間に含まれていれば、最大値あるいは最小値になっているかを確認していきます。つまり、
$$
\mathrm{max} \leq f(x_1) \Rightarrow \mathrm{max} = f(x_1), \ x_{\mathrm{max}} = x_1 \\
\mathrm{min} \geq f(x_1) \Rightarrow \mathrm{min} = f(x_1), \ x_{\mathrm{min}} = x_1
$$
として、$${\mathrm{max}, \mathrm{min} }$$や$${x_{\mathrm{max}}, x_{\mathrm{min}}}$$を更新していきます。もう一つの極値の位置$${x_2}$$についても同様に確認します。
④ 区間の右端$${r}$$での3次関数の値$${f(r)}$$が最大値あるいは最小値になっているかを確認します。つまり、
$$
\mathrm{max} < f(r) \Rightarrow \mathrm{max} = f(r), \ x_{\mathrm{max}} = r \\
\mathrm{min} > f(r) \Rightarrow \mathrm{min} = f(r), \ x_{\mathrm{min}} = r
$$
として、$${\mathrm{max}, \mathrm{min} }$$や$${x_{\mathrm{max}}, x_{\mathrm{min}}}$$を更新していきます。
⑤ 最後に最大値や最小値の位置が区間に含まれているかを再確認しておきます。
今回の例のように、$${l \leq x \leq r}$$と区間の両端が含まれる形の場合は、①から④までの処理で得られた最大値や最小値がそのまま答えとなります。一方、区間の両端が含まれない$${l < x < r}$$と設定される場合は注意が必要です。①から④までの処理で、区間の端(つまり、$${l}$$または$${r}$$)が最大値または最小値の位置となっていると、これらの位置は区間に含まれていないので、最大値や最小値ではないことになります。これを最後に判別しておきます。
プログラム
それでは、3次関数の最大値・最小値を求めるプログラムを作成します。ここでは、問題(1)を例として作成します。
今回は、記事『高校数学をプログラミングで解く(数学II編)「5-3 関数の値の変化」』で作成したスケッチ「calcandplotExtrema」を再利用して作成していきます。
スケッチ「calcandplotExtrema」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「calcandplotMaxandMin」と変更し、またスケッチ「calcandplotMaxandMin」内の「calcandplotExtrema.pde」ファイルの名前を「calcandplotMaxandMin.pde」に変更します。そして、pdeファイル「calcandplotMaxandMin.pde」をダブルクリックしてスケッチ「calcandplotMaxandMin」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「calcandplotMaxandMin」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 100.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
// 区間
float left_endpoint = -4.0; // 区間の左端
float right_endpoint = 4.0; // 区間の右端
boolean including_left_endpoint = true; // 区間の左端を含むか
boolean including_right_endpoint = true; // 区間の右端を含むか
// 3次関数の係数
float a = 1.0; // x^3の係数
float b = 0.0; // x^2の係数
float c = -27.0; // xの係数
float d = 0.0; // 定数項
// 3次関数を描く
stroke(0,0,0);
draw_cubic_function(a,b,c,d,left_endpoint,right_endpoint);
// 極値を計算してプロットする
calc_and_plot_max_and_min(
a,b,c,d,
left_endpoint,
right_endpoint,
including_left_endpoint,
including_right_endpoint
);
// save("extrema.jpg");
}
// 3次関数
float f(
float a, // x^3の係数
float b, // x^2の係数
float c, // xの係数
float d, // 定数項
float x
){
return a*x*x*x + b*x*x + c*x + d;
}
// 3次関数を描く関数
void draw_cubic_function(
float a, // x^3の係数
float b, // x^2の係数
float c, // xの係数
float d, // 定数項
float x_min, // グラフの定義域の下限
float x_max // グラフの定義域の上限
){
int plot_num = 2000; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=1; i<plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
y = f(a,b,c,d,x); // 曲線上の点のyの値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}
// xが区間に含まれているかを判別する関数
boolean in_interval(
float left_endpoint, // 区間の左端
float right_endpoint, // 区間の右端
boolean including_left_endpoint, // 区間の左端を含むか
boolean including_right_endpoint, // 区間の右端を含むか
float x // 判別したい数
){
if( ( x > left_endpoint && x < right_endpoint )
|| ( including_left_endpoint && x == left_endpoint )
|| ( including_right_endpoint && x == right_endpoint )
) {
return true;
} else {
return false;
}
}
// 最大値、最小値を計算してプロットする関数
void calc_and_plot_max_and_min(
float a, // x^3の係数
float b, // x^2の係数
float c, // xの係数
float d, // 定数項
float left_endpoint, // 区間の左端
float right_endpoint, // 区間の右端
boolean including_left_endpoint, // 区間の左端を含むか
boolean including_right_endpoint // 区間の右端を含むか
){
// 最大値、最小値の初期化
float x_max = left_endpoint;
float x_min = left_endpoint;
float maximum = f(a,b,c,d,left_endpoint);
float minimum = f(a,b,c,d,left_endpoint);
// f'(x)=0(2次方程式)の判別式を計算する
float D = (2.0*b)*(2.0*b)-4.0*(3.0*a)*c;
// 2つの極値をもつとき、極値が最大値、最小値になっているか確認
if( D > 0.0 ){
// 1つ目の極値
float x1 = (-(2.0*b)-sqrt(D))/2.0/(3.0*a);
float y1 = f(a,b,c,d,x1);
// x1が指定されている区間に含まれれば、
// 最大値、最小値になっているか確認
if(
in_interval(
left_endpoint,
right_endpoint,
including_left_endpoint,
including_right_endpoint,
x1
)
){
if( maximum <= y1 ){ // 最大値の候補か確認
maximum = y1;
x_max = x1;
}
if( minimum >= y1 ){ // 最小値の候補か確認
minimum = y1;
x_min = x1;
}
}
// 2つ目の極値
float x2 = (-(2.0*b)+sqrt(D))/2.0/(3.0*a);
float y2 = f(a,b,c,d,x2);
// x2が指定されている区間に含まれれば、
// 最大値、最小値になっているか確認
if(
in_interval(
left_endpoint,
right_endpoint,
including_left_endpoint,
including_right_endpoint,
x2
)
){
if( maximum <= y2 ){ // 最大値の候補か確認
maximum = y2;
x_max = x2;
}
if( minimum >= y2 ){ // 最小値の候補か確認
minimum = y2;
x_min = x2;
}
}
}
// 区間の右端が最大値、最小値になっているか確認
float y_right = f(a,b,c,d,right_endpoint);
if( maximum < y_right ){ // 最大値の候補か確認
maximum = y_right;
x_max = right_endpoint;
}
if( minimum > y_right ){ // 最小値の候補か確認
minimum = y_right;
x_min = right_endpoint;
}
// x_maxが指定された区間に入っているか確認して出力する
if(
in_interval(
left_endpoint,
right_endpoint,
including_left_endpoint,
including_right_endpoint,
x_max
)
){
stroke(255,0,0);
println("最大値:", x_max, maximum);
plot_max_min_point(a,b,c,d,x_max);
} else {
println("最大値なし");
}
// x_minが指定された区間に入っているか確認して出力する
if(
in_interval(
left_endpoint,
right_endpoint,
including_left_endpoint,
including_right_endpoint,
x_min
)
){
stroke(0,255,0);
println("最小値:", x_min, minimum);
plot_max_min_point(a,b,c,d,x_min);
} else {
println("最小値なし");
}
}
// 最大値・最小値をプロットする関数
void plot_max_min_point(
float a, // x^3の係数
float b, // x^2の係数
float c, // xの係数
float d, // 定数項
float x // 最大値・最小値のx座標
){
float y = f(a,b,c,d,x);
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード1 3次関数の最大値・最小値を求めるプログラム
ソースコード1で、3次関数$${f(x)=ax^3+bx^2+cx+d}$$とその3次関数を描く関数は、記事『高校数学をプログラミングで解く(数学II編)「5-3 関数の値の変化」』のスケッチ「calcandplotExtrema」内で作成した f 関数と draw_cubic_function 関数をそのまま再利用しています。
最大値、最小値を計算してプロットする関数 calc_and_plot_max_and_min は、アルゴリズム設計のところで解説した処理の流れの通りに作成しています。なお、$${x}$$が区間に含まれているかを判別する処理は、calc_and_plot_max_and_min 関数内でもしばしば利用されるので、in_interval 関数として準備しました。in_interval 関数の引数として、区間の端点となる left_endpoint, right_endpoint ($${l}$$と$${r}$$に対応)だけでなく、それらの端点が区間に含まれるかどうかを示すフラグ including_left_endpoint, including_right_endpoint を導入することで、閉区間$${l \leq x \leq r}$$と開区間$${l < x < r}$$と両方に対応できるようにしています。
ソースコード1を、スケッチ「calcandplotMaxandMin」の「calcandplotMaxandMin」タブのテキストエディタ部分に書いて実行すると、図2のように、実行ウィンドウのキャンバス上に問題(1)の3次関数(黒色)とその関数の最大値(赤色)、最小値(青色)が描かれます。なお、今回は$${y}$$軸方向の表示範囲を$${-100}$$から$${100}$$までに設定しています。

また、図3のように、開発環境ウィンドウのコンソールに、
最大値: -3.0 54.0
最小値: 3.0 -54.0
と、最大値、最小値の位置とその値が出力されます。

その他の問題のプログラム
他の問題(2)-(4)については、ソースコード1の
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 100.0; // y軸の表示範囲 -y_rangeからy_rangeまで の部分と
// 区間
float left_endpoint = -4.0; // 区間の左端
float right_endpoint = 4.0; // 区間の右端
boolean including_left_endpoint = true; // 区間の左端を含むか
boolean including_right_endpoint = true; // 区間の右端を含むか
// 3次関数の係数
float a = 1.0; // x^3の係数
float b = 0.0; // x^2の係数
float c = -27.0; // xの係数
float d = 0.0; // 定数項の部分を問題に合わせて書き換えて、実行するだけで3次関数のグラフとその最大値、最小値を描くことができます。
問題(2)
問題(2)のグラフは、図4のようになります。

また、開発環境ウィンドウのコンソールには、
最大値: 0.0 0.0
最小値: -1.0 -2.0
と出力されます。
実は、この結果は正しいとは言えません。実際には、最大値は$${x=0}$$と$${x=1}$$の2箇所で$${0}$$の値を取ります。正しい処理をさせるためには、複数の箇所に最大値または最小値を取る場合にも対応できるようにプログラム(ソースコード1)を修正する必要があります。是非チャレンジしてみてください。
問題(3)
問題(3)のグラフは、図5のようになります。
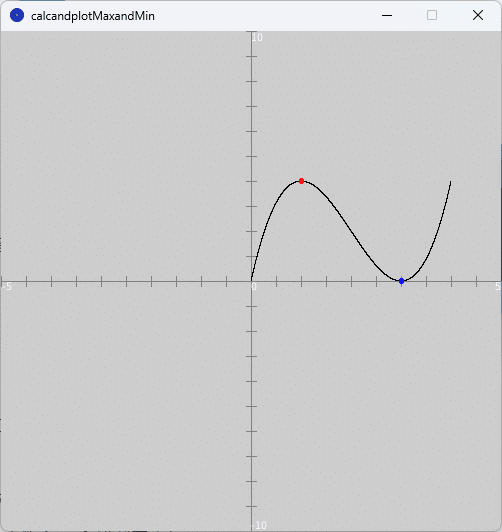
また、開発環境ウィンドウのコンソールには、
最大値: 1.0 4.0
最小値: 3.0 0.0
と出力されます。図5のグラフをみると、左の端点$${x=0}$$での値が最小値の候補、右の端点$${x=4}$$での値が最大値の候補になるように見えますが、今回の区間は端点を含まない開区間となっているため、$${x=0}$$での最小値候補や$${x=4}$$での最大値候補はそれぞれ最小値、最大値ではなくきちんと除外されています。
問題(4)
問題(4)のグラフは、図6のようになります。

また、開発環境ウィンドウのコンソールには、
最大値なし
最小値: 2.0 -2.0
と出力されます。図6のグラフをみると、右の端点$${x=3}$$が最大値の候補になりますが、今回の区間は端点を含まない開区間となっているため、$${x=3}$$での値は最大値になりません。
まとめ
今回は、数学IIで学ぶ「関数の最大値・最小値」について、特に3次関数に対する最大値・最小値を求め、3次関数のグラフに最大値・最小値を取る点をプロットするプログラムを作成しました。
関数の最大値・最小値を求めることは、記事『高校数学をプログラミングで解く(数学I編)「1-4 2次関数の最大と最小」』でもすでに行っています。このときは、区間を分割し、それらの分割点すべてにおける関数の値を比較して一番大きな値、または一番小さな値をそれぞれ最大値、最小値としました。一方で今回、関数の区間の端点での値と極値のみを比較することで最大値、最小値を求めることができました。つまり、最大値や最小値を求めるために関数のすべての点での値を計算する必要はなく、区間の端点と関数の極値のみ計算すればよいということです。
ただし、今回のプログラムでは複数個所で最大値や最小値を取る場合には対応していません。これに対応できるようにアルゴリズムやプログラムを修正することは結構勉強になると思いますので、ぜひチャレンジしてみてください。
参考文献
改訂版 教科書傍用 スタンダード 数学II(数研出版、ISBN9784410209369)
この記事が気に入ったらサポートをしてみませんか?
