高校数学をプログラミングで解く（数学II編）「5-3 関数の値の変化」

2024年4月3日 06:31

はじめに

今回は、数学IIで学ぶ「関数の値の変化」について、特に３次関数に対する極値を求め、３次関数のグラフに極値を取る点をプロットするプログラムを作成します。

関数の値の変化

まず、関数の増減、関数の極大・極小について解説しておきます。

関数の増減

ある区間で、常に$${f'(x) > 0}$$ならば、$${f(x)}$$はその区間で単調に増加する。
ある区間で、常に$${f'(x) < 0}$$ならば、$${f(x)}$$はその区間で単調に減少する。
ある区間で、常に$${f'(x) = 0}$$ならば、$${f(x)}$$はその区間で定数である。

関数の極大・極小

$${x}$$の整式で表された関数$${f(x)}$$の$${x=a}$$を含む十分小さな区間を考える。
$${x = a}$$で極大 $${ \Leftrightarrow }$$ $${f'(x)}$$の符号が$${x=a}$$の前後で 正から負 に変わる。
$${x = a}$$で極小 $${ \Leftrightarrow }$$ $${f'(x)}$$の符号が$${x=a}$$の前後で 負から正 に変わる。
注意
$${x=a}$$で極値をとれば$${f'(a) = 0}$$である。しかし、$${f'(a)=0}$$であっても$${x=a}$$で極値をとるとは限らない。　例）$${f(x) = x^3}$$

関数の極大・極小を計算する

今回は、特に３次関数に対する極値を求め、３次関数のグラフに極値を取る点をプロットするプログラムを作成します。

問題
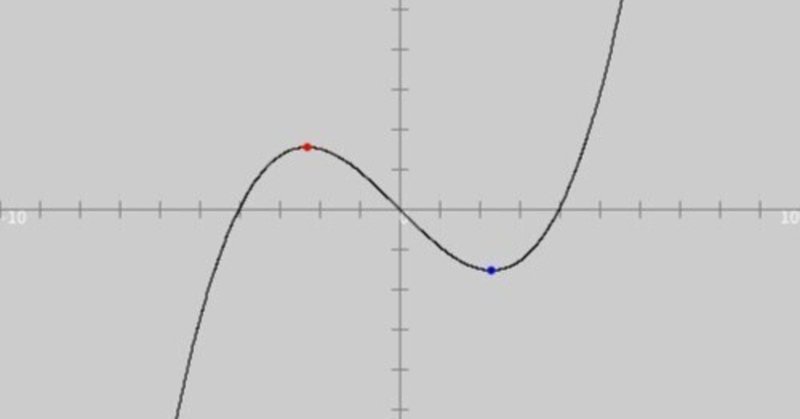
次の３次関数の極値を求め、そのグラフを描き、極値をプロットせよ。
(1) $${y=2x^3-3x^2+1}$$
(2) $${y=-x^3+3x+1}$$
(3) $${y=x^3+x}$$

アルゴリズム設計

今回の問題は３次関数の極値に特化しているので、そのことを利用して極値を求めます。つまり、３次関数

$$
y=f(x) = ax^3+bx^2+cx+d \ \ (a \neq 0)
$$

の導関数は２次関数

$$
f'(x) = 3ax^2 + 2bx +c
$$

になりますので、２次方程式$${f'(x)=0}$$を解の公式を用いて、2つの実数解$${x_1, x_2}$$を求めることができれば、それら$${x_1, x_2}$$の位置に極値があることがわかります。あとは、それら$${x_1, x_2}$$の前後の位置での導関数の値$${f'(x_1-e)}$$と$${f'(x_1+e)}$$、$${f'(x_2-e)}$$と$${f'(x_2+e)}$$の符号を調べることで、極値が極大値なのか、極小値なのかを決定することができます。ここで、$${e}$$は十分小さな正の数を表しています。

プログラム

それでは、３次関数に対する極値を求め、３次関数のグラフに極値を取る点をプロットするプログラムを作成します。ここでは、問題(1)を例として作成します。
今回は、記事『高校数学をプログラミングで解く（数学II編）「5-2 接線」』で作成したスケッチ「drawTangentialLine」を再利用して作成していきます。
スケッチ「drawTangentialLine」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「calcandplotExtrema」と変更し、またスケッチ「calcandplotExtrema」内の「drawTangentialLine.pde」ファイルの名前を「calcandplotExtrema.pde」に変更します。そして、pdeファイル「calcandplotExtrema.pde」をダブルクリックしてスケッチ「calcandplotExtrema」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「calcandplotExtrema」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  
  // ３次関数の係数
  float a = 2.0;  // x^3の係数
  float b = -3.0;  // x^2の係数
  float c = 0.0;  // xの係数
  float d = 1.0;  // 定数項
    
  // ３次関数を描く
  stroke(0,0,0);  
  float x_min = -x_range;
  float x_max = x_range;
  draw_cubic_function(a,b,c,d,x_min, x_max);

  // 極値を計算してプロットする
  calc_and_plot_extrema(a,b,c,d);

}

// ３次関数
float f(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数
  float d, // 定数項
  float x 
){
  return a*x*x*x + b*x*x + c*x + d;
}

// ３次関数の導関数
float f_prime(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数
  float x
){
  return 3.0*a*x*x + 2.0*b*x + c;
}

// ３次関数を描く関数
void draw_cubic_function(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数  
  float d,  // 定数項
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = f(a,b,c,d,x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 極値を計算してプロットする関数
void calc_and_plot_extrema(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数  
  float d  // 定数項
){
  // 極値前後の小さな区間[x-e,x+e]
  float e = 0.01;
  // f'(x)=0（２次方程式）の判別式を計算する
  float D = (2.0*b)*(2.0*b)-4.0*(3.0*a)*c;
  if( D > 0.0 ){ // 2つの極値をもつとき
    // 1つ目の極値
    float x1 = (-(2.0*b)-sqrt(D))/2.0/(3.0*a);
    float y1 = f(a,b,c,d,x1);
    float before_x1 = f_prime(a,b,c,x1-e);
    float after_x1 = f_prime(a,b,c,x1+e);
    if( before_x1 > 0.0 && after_x1 < 0.0 ){
      // 極大値であれば赤色でプロット
      stroke(255,0,0);
      println("極大値:", x1, y1);
    } else if(before_x1 < 0.0 && after_x1 > 0.0 ){
      // 極小値であれば青色でプロット
      stroke(0,0,255);
      println("極小値:", x1, y1);
    } else {
      // 極値でなければ緑色でプロット
      stroke(0,255,0);
      println("極値ではない:", x1, y1);
    }
    plot_extrema_point(a,b,c,d,x1);
    
    // 2つ目の極値
    float x2 = (-(2.0*b)+sqrt(D))/2.0/(3.0*a);
    float y2 = f(a,b,c,d,x2);
    float before_x2 = f_prime(a,b,c,x2-e);
    float after_x2 = f_prime(a,b,c,x2+e);
    if( before_x2 > 0.0 && after_x2 < 0.0 ){
      // 極大値であれば赤色でプロット
      stroke(255,0,0);
      println("極大値:", x2, y2);
    } else if(before_x2 < 0.0 && after_x2 > 0.0 ){
      // 極小値であれば青色でプロット
      stroke(0,0,255);
      println("極小値:", x2, y2);
    } else {
      // 極値でなければ緑色でプロット
      stroke(0,255,0);
      println("極値ではない:", x2, y2);
    }
    plot_extrema_point(a,b,c,d,x2);
    
  } else { // D ≦ 0　の場合
    println("極値なし");
  }
  
}

// 極値をプロットする関数
void plot_extrema_point(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数  
  float d, // 定数項
  float x // 極値のx座標
){
  float y = f(a,b,c,d,x);
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード1　３次関数に対する極値を求め、３次関数のグラフに極値を取る点をプロットするプログラム

ソースコード1で、３次関数$${f(x)=ax^3+bx^2+cx+d}$$とその導関数$${f'(x)=3ax^2+2bx+c}$$をそれぞれ f 関数と f_prime 関数として準備しました。また、３次関数を描く関数 draw_cubic_function と極値をプロットする関数 plot_extrema_point は、記事『高校数学をプログラミングで解く（数学II編）「5-2 接線」』のスケッチ「drawTangentialLine」内で作成した曲線を描く関数 draw_curve_function と接線を描く関数 draw_tangential_line を引数のみ調整して再利用して作成しています。
極値を計算してプロットする関数 calc_and_plot_extrema は、アルゴリズム設計のところで解説した通りに作成していますが、一点、関数の極大・極小の解説時に注意として記載した「$${f'(a)=0}$$であっても$${x=a}$$で極値をとるとは限らない。」を考慮して、極値がない場合も場合分けの選択肢として準備しました。

ソースコード1を、スケッチ「calcandplotExtrema」の「calcandplotExtrema」タブのテキストエディタ部分に書いて実行すると、図1のように、実行ウィンドウのキャンバス上に問題(1)の３次関数（黒色）とその関数の極大値（赤色）、極小値（青色）が描かれます。

また、図2のように、開発環境ウィンドウのコンソールに、

極大値: 0.0 1.0
極小値: 1.0 0.0

と、極大値、極小値の位置とその値が出力されます。

その他の問題のプログラム

他の問題(2),(3)については、ソースコード1の

  // ３次関数の係数
  float a = 2.0;  // x^3の係数
  float b = -3.0;  // x^2の係数
  float c = 0.0;  // xの係数
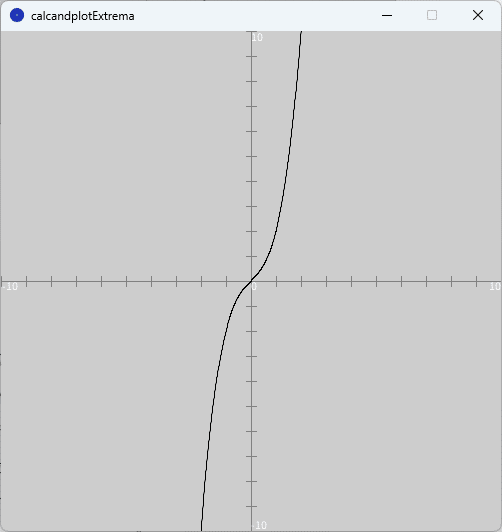
  float d = 1.0;  // 定数項

を問題に合わせて書き換えて、実行するだけで３次関数のグラフとその極値を描くことができます。そのため、問題(2),(3)については結果のグラフのみを示しておきます。なお、問題(3)は「極値なし」ですので、３次関数のグラフのみとなっています（図4参照）。

まとめ

今回は、数学IIで学ぶ「関数の値の変化」について、特に３次関数に対する極値を求め、３次関数のグラフに極値を取る点をプロットするプログラムを作成しました。
３次関数に特化したので、極値の位置を求める方程式$${f'(x)=0}$$が２次方程式となり、解の公式を利用して解くことができました。$${f(x)}$$がより高次の関数になった場合、解析的に解くことは難しくなってきます。そのときは、記事『高校数学をプログラミングで解く（数学II編）「5-1 微分係数、導関数」』で説明した数値微分を利用しましょう。上記の問題も数値微分で解くこともできますので、是非チャレンジしてみてください。

参考文献

改訂版教科書傍用スタンダード数学II（数研出版、ISBN9784410209369）

この記事が気に入ったらサポートをしてみませんか？