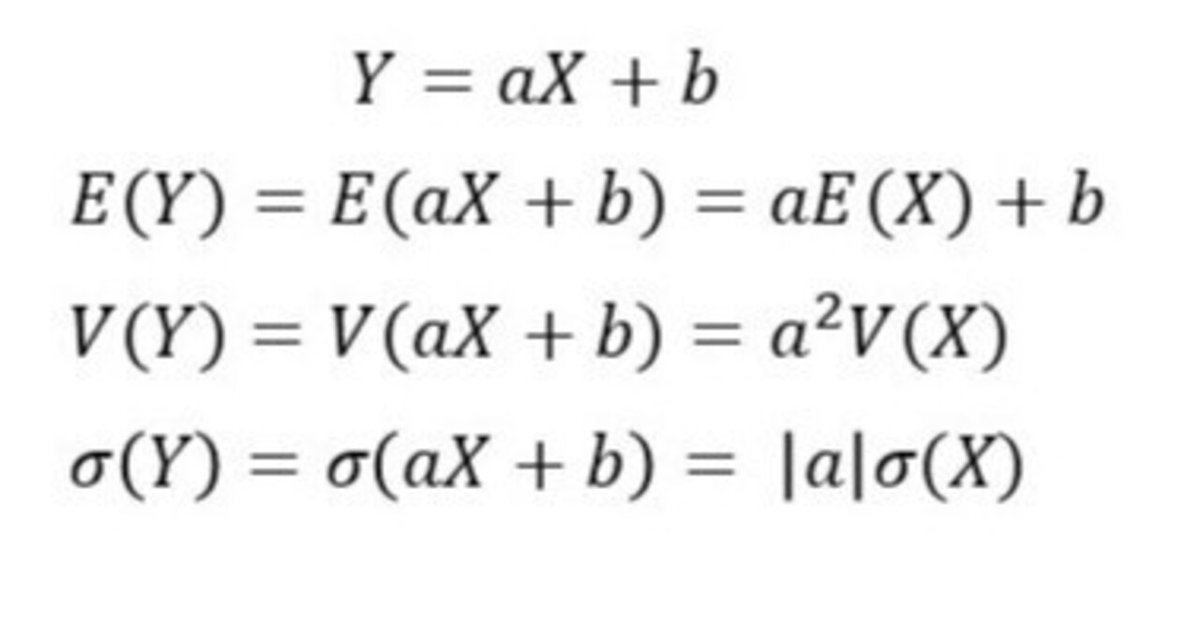
高校数学をプログラミングで解く（数学B編）「4-3 確率変数の変換」

はじめに

今回は、数学Bで学ぶ「確率変数の変換」について、変換された確率変数$${Y}$$に対する期待値と分散を求めるプログラムを２つの方法を用いて作成します。

確率変数の変換

まず、確率変換の変換について復習しておきます。

確率変数$${X}$$と定数$${a, b}$$に対して$${Y=aX+b}$$とすると、$${Y}$$も確率変数となり、
期待値　　$${E(Y)=E(aX+b)=aE(X)+b}$$
分散　　　$${V(Y)=V(aX+b)=a^2V(X)}$$
標準偏差　$${\sigma(Y) = \sigma(aX+b) = |a| \sigma(X) }$$

変換した確率変数での期待値を計算する

今回は次のような問題を考えてみます。

問題
数直線上の原点に点$${\mathrm{P}}$$がある。1枚の硬貨を投げて、表が出ると+3だけ、裏が出ると-2だけ進む。この試行を3回繰り返すときの表の出た回数を$${X}$$、点$${\mathrm{P}}$$の座標を$${Y}$$とする。
(1) $${Y}$$を$${X}$$で表せ。
(2) $${Y}$$の期待値と分散を求めよ。

なお、今回は2つの方法で$${Y}$$の期待値と分散を計算してみます。1つ目は確率変数$${X}$$、変換した確率変数$${Y}$$に対する確率分布を求めて、直接、確率変数$${Y}$$の期待値と分散を計算します。2つ目は確率変数$${X}$$の期待値と分散を計算した後、上記で説明した「確率変数$${X}$$の期待値と分散」と「確率変数$${Y}$$の期待値と分散」との関係式を利用して確率変数$${Y}$$の期待値と分散を計算してみます。

アルゴリズム設計 

まず、問題の「(1) $${Y}$$を$${X}$$で表せ。」を考えます。3回繰り返すときの表の出た回数を$${X}$$としているので、3回繰り返すときの裏の出た回数は$${3-X}$$となります。一方、$${Y}$$の値は、「表が出ると+3だけ、裏が出ると-2だけ進む」となっていますので、

$$
Y= (+3) \times X + (-2) \times (3-X) = 5X-6
$$

となります。この関係式を利用して確率変数$${X}$$、変換した確率変数$${Y}$$に対する確率分布を求めてみます。

$$
\begin{array}{c||cccc|c}
\hline
X & 0 & 1 & 2 & 3 & \mathrm{計} \\
\hline
Y & -6 & -1 & 4 & 9 & \\
\hline
P & \frac{1}{8} & \frac{3}{8} & \frac{3}{8} & \frac{1}{8} & 1 \\
\hline
\end{array}
$$

この表を利用すると、確率変数の期待値と分散の計算を行うことができます。

プログラム１（直接計算）

では、変換した確率変数$${Y}$$に対して期待値と分散を計算するプログラムを作成していきます。

// 変換された確率変数の期待値と分散の計算
void setup(){

  // 変換された確率変数の値
  int[] y = {-6,-1,4,9};
  // 確率分布P
  float[] p = {1.0/8.0, 3.0/8.0, 3.0/8.0, 1.0/8.0};

  // 変換された確率変数の期待値の計算
  float m_y = 0;
  for(int i=0;i<y.length;i++){
    m_y = m_y + y[i]*p[i];
  }
  
  // 変換された確率変数の分散の計算
  float v_y = 0;
  for(int i=0;i<y.length;i++){
    v_y = v_y + (y[i]-m_y)*(y[i]-m_y)*p[i];
  }
  
  // 変換された確率変数の期待値と分散の値をコンソールに出力
  println("期待値　：", m_y);
  println("分散　　：", v_y);
  
}

ソースコード1　変換された確率変数の期待値と分散を計算するプログラム

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「transformedProbabilityVariable」としています）、テキストエディタ部分に書いて実行します。

図1　スケッチ「transformedProbabilityVariable」の実行結果

図1のように、確率変数$${Y}$$の期待値と分散を

期待値　： 1.5
分散　　： 18.75

のようにコンソールに出力します。なお、これらの値は分数で表すと順に

$$
\frac{3}{2}, \frac{75}{4}
$$

となっています。

プログラム２（公式利用）

次に、確率変数$${X}$$の期待値と分散を計算した後、関係式を利用して確率変数$${Y}$$の期待値と分散を計算するプログラムを作成します。

// 関係式を用いた、変換された確率変数の期待値と分散の計算
void setup(){

  // 確率変数の値
  int[] x = {0,1,2,3}; 
  // 確率分布P
  float[] p = {1.0/8.0, 3.0/8.0, 3.0/8.0, 1.0/8.0};

  // 確率変数を変換するときの係数
  int a = 5;
  int b = -6;

  // 確率変数Xの期待値の計算
  float m_x = 0;
  for(int i=0;i<x.length;i++){
    m_x = m_x + x[i]*p[i];
  }
  
  // 確率変数Xの分散の計算
  float v_x = 0;
  for(int i=0;i<x.length;i++){
    v_x = v_x + (x[i]-m_x)*(x[i]-m_x)*p[i];
  }
  
  // 変換された確率変数Yの期待値と分散の計算
  float m_y = a * m_x + b;
  float v_y = a * a * v_x;
  
  // 変換された確率変数の期待値と分散の値をコンソールに出力
  println("期待値　：", m_y);
  println("分散　　：", v_y);
  
}

ソースコード2　関係式を用いた期待値と分散を計算するプログラム

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「transformedProbabilityVariable2」としています）、テキストエディタ部分に書いて実行します。

図2　スケッチ「transformedProbabilityVariable2」の実行結果

図2のように、確率変数$${Y}$$の期待値と分散を

期待値　： 1.5
分散　　： 18.75

のようにコンソールに出力します。もちろん、結果は直接計算した場合と同じになります。

まとめ

今回は、数学Bで学ぶ「確率変数の変換」について、変換された確率変数$${Y}$$に対する期待値と分散を求めるプログラムを２つの方法を用いて作成しました。
1つ目は変換した確率変数$${Y}$$に対する確率分布を求めて、直接、確率変数$${Y}$$の期待値と分散を計算する方法でプログラムを作成しました。2つ目は確率変数$${X}$$の期待値と分散を計算した後、関係式を利用して確率変数$${Y}$$の期待値と分散を計算するプログラムを作成しました。
今回の場合は、どちらでもあまりかわからない計算量でしたが、基本は２つ目の関係式を用いた方法がよいでしょう。変換した確率変数が$${Y}$$だけでなく、新たに$${Z}$$などと増えていった場合、確率変数$${X}$$の期待値と分散がわかっていれば、あとは$${Y}$$や$${Z}$$の期待値は関係式から得られるからです。
どちらが良いかは経験を積んでいけばわかるようになってくるので、どんどんプログラミングをやってみてください。

参考文献

改訂版 教科書傍用 スタンダード 数学B（数研出版、ISBN9784410209468）