高校数学をプログラミングで解く（数学B編）「1-4 ベクトルと図形」

2024年5月8日 06:30

マガジンリスト　＞　数学B編 1.平面上のベクトル　＞　1-4 ベクトルと図形

はじめに

今回は、数学Bで学ぶ「ベクトルと図形」について、ベクトルと図形に関する性質の応用例として、三角形の内心の位置ベクトルを計算して、座標上に描くプログラムを作成します。

ベクトルと図形に関する性質

まず、ベクトルと図形に関する性質についてまとめておきます。

一直線上の3点
２点$${\mathrm{A, B}}$$が異なるとき
点$${\mathrm{P}}$$が直線$${\mathrm{AB}}$$上にある $${ \Leftrightarrow }$$ $${ \overrightarrow{ \mathrm{AP} } = k \overrightarrow{ \mathrm{AB} } }$$となる実数$${k}$$がある

ベクトルの相等
$${ s, t, s', t' }$$は実数とする。
$${ \vec{a} \neq \vec{0}, \ \vec{b} \neq \vec{0}, \ \vec{a} / \!\! / \!\!\!\!\! \backslash \vec{b} }$$のとき、

$$
s \vec{a} + t \vec{b} = s' \vec{a} + t' \vec{b} \Leftrightarrow s = s', \ t = t'
$$

特に

$$
s \vec{a} + t \vec{b} = \vec{0} \Leftrightarrow s=t=0
$$

三角形の内心の位置ベクトルを求める

今回は、上記で説明したベクトルと図形に関する性質を利用して、三角形の内心の位置ベクトルを求めて、それを描画するプログラムを作成します。

三角形の内心（復習）

三角形の内心は「３つの内角の二等分線が交わる点」となります（図1）。

三角形の内心はその三角形の内接円の中心となります。

内心の位置ベクトルの導出

図1のように$${\triangle \mathrm{ABC}}$$を準備します。
$${\triangle \mathrm{ABC}}$$の各頂点の位置ベクトルをそれぞれ$${ \mathrm{A}( \vec{a} ), \mathrm{B}( \vec{b} ), \mathrm{C}( \vec{c} ) }$$とし、また、△ABCの内心の位置ベクトルを$${ \mathrm{I}( \vec{i} ) }$$とします。

① 内心の定義から、内心$${\mathrm{I}}$$は内角$${\mathrm{A}}$$の二等分線上にあるので、ベクトルと図形に関する性質「一直線上の３点」により、実数$${s}$$を用いて

$$
\overrightarrow{ \mathrm{AI} } = s \left(
\frac{ \overrightarrow{ \mathrm{AB} } }{ \left| \overrightarrow{ \mathrm{AB} } \right| }
+ \frac{ \overrightarrow{ \mathrm{AC} } }{ \left| \overrightarrow{ \mathrm{AC} } \right| }
\right)
$$

と表すことができます。また、内心$${\mathrm{I}}$$は内角$${\mathrm{B}}$$の二等分線上にもあるので、実数$${t}$$を用いて

$$
\overrightarrow{ \mathrm{BI} } = t \left(
\frac{ \overrightarrow{ \mathrm{BA} } }{ \left| \overrightarrow{ \mathrm{BA} } \right| }
+ \frac{ \overrightarrow{ \mathrm{BC} } }{ \left| \overrightarrow{ \mathrm{BC} } \right| }
\right)
$$

と表すことができます。これらの式は、位置ベクトルを利用して、

$$
\vec{i} - \vec{a} = s \left( \frac{ \vec{b}-\vec{a} }{ \left|\vec{b}-\vec{a} \right| }
+ \frac{ \vec{c}-\vec{a} }{ \left|\vec{c}-\vec{a} \right| }
\right)
$$

と

$$
\vec{i} - \vec{b} = t \left( \frac{ \vec{a}-\vec{b} }{ \left|\vec{a}-\vec{b} \right| }
+ \frac{ \vec{c}-\vec{b} }{ \left|\vec{c}-\vec{b} \right| }
\right)
$$

と書き換えることができます。

② ①で求めた２式の両辺の差を取ると、左辺は、

$$
\mathrm{左辺の差} = \vec{b}-\vec{a} = (\vec{b}-\vec{c}) - (\vec{a}-\vec{c})
$$

となり、右辺は

$$
\mathrm{右辺の差} = \left( \frac{s+t}{ \left|\vec{b}-\vec{a} \right| }
+\frac{t}{ \left|\vec{c}-\vec{b} \right| } \right) ( \vec{b}-\vec{c} )
-\left( \frac{s+t}{ \left|\vec{b}-\vec{a} \right| }
+\frac{s}{ \left|\vec{a}-\vec{c} \right| } \right) ( \vec{a}-\vec{c} )
$$

となります。これらの両辺を比較すると、$${ \vec{a}-\vec{c} \neq \vec{0}, \ \vec{b}-\vec{c} \neq \vec{0}, \ \vec{a}-\vec{c} / \!\! / \!\!\!\!\! \backslash \vec{b}-\vec{c} }$$であるので、ベクトルと図形に関する性質「ベクトルの相等」により

$$
\frac{s+t}{ \left|\vec{b}-\vec{a} \right| }
+\frac{t}{ \left|\vec{c}-\vec{b} \right| } = 1,
\frac{s+t}{ \left|\vec{b}-\vec{a} \right| }
+\frac{s}{ \left|\vec{a}-\vec{c} \right| } = 1
$$

の２式が得られます。これらの２式から、$${s, t}$$はそれぞれ

$$
s = \frac{\left|\vec{b}-\vec{a} \right| \left|\vec{a}-\vec{c} \right|}{\left|\vec{b}-\vec{a} \right|+\left|\vec{c}-\vec{b} \right|+\left|\vec{a}-\vec{c} \right| },
t = \frac{\left|\vec{b}-\vec{a} \right| \left|\vec{c}-\vec{b} \right|}{\left|\vec{b}-\vec{a} \right|+\left|\vec{c}-\vec{b} \right|+\left|\vec{a}-\vec{c} \right| },
$$

となります。最後に、

$$
p=\left|\vec{b}-\vec{a} \right|+\left|\vec{c}-\vec{b} \right|+\left|\vec{a}-\vec{c} \right|
$$

とおくと、内心の位置ベクトル$${\vec{i}}$$は

$$
\vec{i} = \frac{1}{p} \left( \left|\vec{c}-\vec{b} \right| \vec{a}+\left|\vec{a}-\vec{c} \right| \vec{b}+\left|\vec{b}-\vec{a} \right| \vec{c} \right)
$$

となります。

内心の位置ベクトルを描くプログラム

三角形の内心の位置ベクトルを求めることができたので、次に三角形の内心の位置ベクトルを描くプログラムを作成していきます。
記事『高校数学をプログラミングで解く（数学B編）「1-0 ベクトルを描く」』で作成したスケッチ「drawVector」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「drawPositionVectorofInnerCenter」と変更し、またスケッチ「drawPositionVectorofInnerCenter」内の「drawVector.pde」ファイルの名前を「drawPositionVectorofInnerCenter.pde」に変更します。そして、pdeファイル「drawPositionVectorofInnerCenter.pde」をダブルクリックしてスケッチ「drawPositionVectorofInnerCenter」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawPositionVectorofInnerCenter」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

// 三角形の内心の位置ベクトルを描く
void setup(){
  size(500,500,P2D);
  noLoop();
  float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
  float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 
  setAxes(x_range, y_range); // 座標軸の準備

  // △ABCの頂点の位置ベクトル
  PVector a = new PVector(1.0, 1.0);
  PVector b = new PVector(7.0, 1.0);
  PVector c = new PVector(3.0, 5.0);
  
  // 三角形ABCの各辺の長さ
  float AB_length = b.copy().sub(a.copy()).mag();
  float BC_length = c.copy().sub(b.copy()).mag();
  float CA_length = a.copy().sub(c.copy()).mag();
  
  // 三角形の周囲の長さ
  float perimeter = AB_length + BC_length + CA_length;
  
  // 内心の位置ベクトル
  PVector i = new PVector(0.0,0.0);
  i.add( a.copy().mult( BC_length / perimeter ) );
  i.add( b.copy().mult( CA_length / perimeter ) );
  i.add( c.copy().mult( AB_length / perimeter ) );
  
  // 以下に図形を描いていく
  noFill(); // 図形の中身を塗りつぶさない

  // △ABCを描く
  stroke(128,128,128);
  triangle(
    a.x * width / 2.0 / x_range, a.y * width / 2.0 / x_range, 
    b.x * width / 2.0 / x_range, b.y * width / 2.0 / x_range, 
    c.x * width / 2.0 / x_range, c.y * width / 2.0 / x_range
  );  
  
  // 三角形の頂点の位置ベクトルの色を黒色に設定
  stroke(0,0,0); 
  // キャンバスにベクトルを描画
  arrow(0.0, 0.0, a.x, a.y, x_range);
  arrow(0.0, 0.0, b.x, b.y, x_range);
  arrow(0.0, 0.0, c.x, c.y, x_range);

  // 内心の位置ベクトルを赤色に設定
  stroke(255,0,0);
  arrow(0.0, 0.0, i.x, i.y, x_range);
}

ソースコード1　内心の位置ベクトルを描くプログラム

なお、今回は△ABCの各頂点の位置ベクトルをそれぞれ、

$$
\vec{a}=(1,1), \ \vec{b}=(7,1), \ \vec{c}=(3,5)
$$

としています。
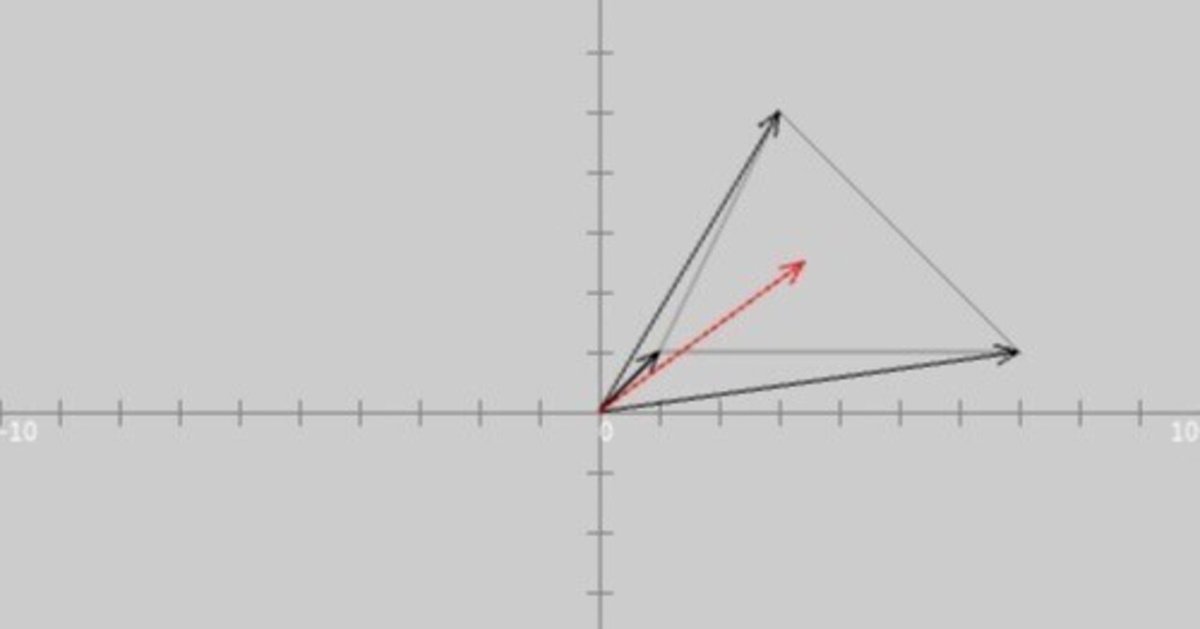
このスケッチ「drawPositionVectorofInnerCenter」を実行すると、図2のように、実行ウィンドウのキャンバスに$${\triangle \mathrm{ABC}}$$が灰色、$${\triangle \mathrm{ABC}}$$の各頂点の位置ベクトル$${\vec{a}, \vec{b}, \vec{c}}$$が黒色の矢印で描かれ、その上に、$${\triangle \mathrm{ABC}}$$の内心の位置ベクトル$${\vec{i}}$$が赤色の矢印で描かれます。

まとめ

今回は、数学Bで学ぶ「ベクトルと図形」について、ベクトルと図形に関する性質の応用例として、三角形の内心の位置ベクトルを計算して、座標上に描くプログラムを作成しました。
三角形の内心の位置ベクトルは、三角形の頂点の位置ベクトル$${\vec{a}, \vec{b}, \vec{c}}$$をそれぞれ実数倍して和を取ったものになりますので、ベクトルと図形に関する性質を学ぶためによい例だと思い、今回説明しました。
三角形の重心の位置ベクトル$${\vec{g}}$$については、

$$
\vec{g} = \frac{ \vec{a}+\vec{b}+\vec{c} }{3}
$$

で与えられます。この重心の位置ベクトルも重心の定義『３つの中線が交わる点』から求めることができますので、一度チャレンジしてみてください。
あと残念ながら、他の三角形の五心である、外心、垂心、傍心は三角形の頂点の位置ベクトルの和では表すことができないようです。ベクトルの外積（ベクトル積）を利用すれば表すことができると思いますが、高校数学の範囲を越えてしまいますので、この記事での説明は割愛します。

参考文献

改訂版教科書傍用スタンダード数学B（数研出版、ISBN9784410209468）

この記事が気に入ったらサポートをしてみませんか？