高校数学をプログラミングで解く（数学II編）「3-5 三角関数の応用」

MK's papa

2024年2月21日 06:01

マガジンリスト　＞　数学Ⅱ編 3.三角関数　＞　3-5 三角関数の応用

はじめに

今回は、数学IIで学ぶ「三角関数の応用」について、三角関数の方程式を解くためのプログラムを作成します。

三角関数の方程式

まず、三角関数の方程式について解説しておきます。

sin関数の方程式

$$
\sin \theta = a \ \ (-1 \leq a \leq 1, \ 0 \leq \theta < 2 \pi)
$$

方程式の左辺と右辺とをそれぞれ$${y = \sin \theta}$$と$${y=a}$$として平面上にグラフを描いて考えます。
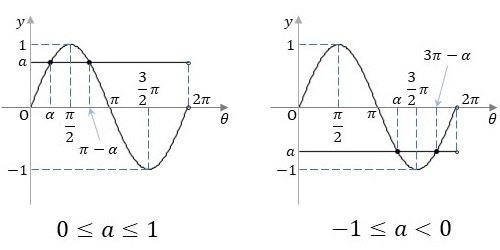
$${0 \leq a \leq 1}$$の場合、これらのグラフは図1の左図のようになります。方程式の解は、$${y = \sin \theta}$$と$${y=a}$$とのグラフの交点の$${\theta}$$成分となります。方程式の解は2つあり、1つの解を$${\alpha}$$とすると、もう一つの解は$${\pi-\alpha}$$となります。
$${-1 \leq a < 0}$$の場合、グラフは図1の右図のようになります。この場合、方程式の2つの解は、1つの解を$${\alpha}$$とすると、もう一つの解は$${3\pi-\alpha}$$となります。

cos関数の方程式

$$
\cos \theta = a \ \ (-1 \leq a \leq 1, \ 0 \leq \theta < 2 \pi)
$$

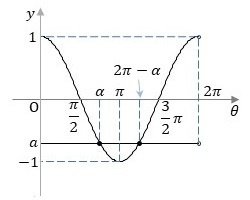
方程式の左辺と右辺とをそれぞれ$${y = \cos \theta}$$と$${y=a}$$として平面上にグラフを描くと図2のようになります。この場合、方程式の2つの解は、1つの解を$${\alpha}$$とすると、もう一つの解は$${2\pi-\alpha}$$となります。

tan関数の方程式

$$
\tan \theta = a \ \ ( 0 \leq \theta < 2 \pi)
$$

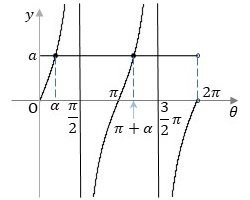
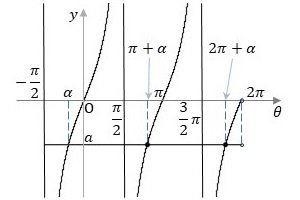
方程式の左辺と右辺とをそれぞれ$${y = \tan \theta}$$と$${y=a}$$として平面上にグラフを描くと図3のようになります。この場合、方程式の2つの解は、1つの解を$${\alpha}$$とすると、もう一つの解は$${\pi+\alpha}$$となります。

asin関数、acos関数、atan関数

上記で方程式をグラフで表したとき、方程式の2つの解は1つの解を$${\alpha}$$とすると、もう一つの解は$${\alpha}$$の式で表されることを説明しましたが、肝心の$${\alpha}$$を求めることについては解説していませんでした。そこで、この$${\alpha}$$を求めることについて解説しておきます。

asin関数

$${\sin \alpha = a \ \ (-1 \leq a \leq 1)}$$となる$${\alpha}$$を求める関数として、asin 関数が用意されています。

float asin(value);

value：$${-1}$$以上$${1}$$以下の実数　float型
返り値：$${-\pi/2}$$以上$${\pi/2}$$以下の実数　float型

この asin 関数を利用すると、以下のようなコードを記述することで、$${\sin \alpha = a}$$となる$${\alpha}$$を求めることができます。

float alpha = asin(a);

ただし、asin 関数の返り値の範囲が$${-\pi/2 \leq \alpha \leq \pi/2}$$であることに注意が必要です。
$${0 \leq a \leq 1}$$の場合、$${\alpha}$$の値は$${0 \leq \alpha \leq \pi/2}$$となり、$${\sin \theta = a}$$の２つの解は、$${\alpha}$$と$${\pi-\alpha}$$となります（図1の左図参照）。
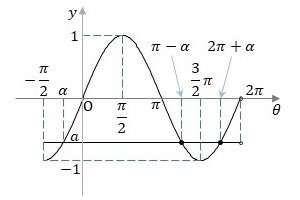
一方、$${-1 \leq a < 0}$$の場合、$${\alpha}$$の値は$${-\pi/2 \leq \alpha < 0}$$になります（図4参照）。今回、解の範囲を$${0 \leq \theta <2\pi}$$としているので、方程式$${\sin \theta = a}$$の2つの解は、$${\pi-\alpha}$$と$${2\pi+\alpha}$$とになります。

acos関数

$${\cos \alpha = a \ \ (-1 \leq a \leq 1)}$$となる$${\alpha}$$を求める関数として、acos 関数が用意されています。

float aoos(value);

value：$${-1}$$以上$${1}$$以下の実数　float型
返り値：$${0}$$以上$${\pi}$$以下の実数　float型

この acos 関数を利用すると、以下のようなコードを記述することで、$${\cos \alpha = a}$$となる$${\alpha}$$を求めることができます。

float alpha = acos(a);

acos 関数の返り値の範囲は$${0 \leq \alpha \leq \pi}$$であり、解の範囲$${0 \leq \theta <2\pi}$$に入っているので、$${\cos \theta = a}$$の２つの解のうち、１つは$${\alpha}$$となり、もう１つは$${2\pi-\alpha}$$となります（図2参照）。

atan関数

$${\tan \alpha = a}$$となる$${\alpha}$$を求める関数として、atan 関数が用意されています。

float atan(value);

value：任意の実数　float型
返り値：$${-\pi/2}$$以上$${\pi/2}$$以下の実数　float型

この atan 関数を利用すると、以下のようなコードを記述することで、$${\tan \alpha = a}$$となる$${\alpha}$$を求めることができます。

float alpha = atan(a);

atan 関数の返り値の範囲が$${-\pi/2 \leq \alpha \leq \pi/2}$$であることに注意してください。
$${a \geq 0}$$の場合、$${\alpha}$$の値は$${0 \leq \alpha \leq \pi/2}$$となり、$${\tan \theta = a}$$の２つの解は、$${\alpha}$$と$${\pi+\alpha}$$となります（図3参照）。
一方、$${a < 0}$$の場合、$${\alpha}$$の値は$${-\pi/2 \leq \alpha < 0}$$になります（図5参照）。今回、解の範囲を$${0 \leq \theta <2\pi}$$としているので、方程式$${\tan \theta = a}$$の2つの解は、$${\pi+\alpha}$$と$${2\pi+\alpha}$$とになります。

三角関数の方程式を解く

では、これらの三角関数の方程式を解くプログラムを作成していきます。

sin関数の方程式を解くプログラム

以下の sin 関数の方程式を解くプログラムを作成します。

$$
\sin \theta = \frac{1}{\sqrt{2}} \ \ (0 \leq \theta < 2\pi)
$$

また、今回のプログラムでは、三角関数の方程式を解くだけでなく、図1のような形でその解をグラフにプロットするようにしてみます。そこで、記事『高校数学をプログラミングで解く（数学II編）「3-4 三角関数のグラフ」』で作成したスケッチ「draw_sin_curve」を再利用します。スケッチ「draw_sin_curve」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「calc_sin_equation」と変更し、またスケッチ「calc_sin_equation」内の「draw_sin_curve.pde」ファイルの名前を「calc_sin_equation.pde」に変更します。そして、pdeファイル「calc_sin_equation.pde」をダブルクリックしてスケッチ「calc_sin_equation」の開発環境ウィンドウを立ち上げます。
開発環境ウィンドウのタブ欄で「calc_sin_equation」タブを選択して、そのテキストエリアのソースコードを以下のような記述に変更します。

// 方程式 sinθ=a (-1≦a≦1, 0≦θ＜2π)を解く

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 4.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  // 方程式の左辺の値
  float a = 1.0/sqrt(2.0);

  // 定義域
  float x_min = 0.0;
  float x_max = 2.0*PI;

  // 方程式 sinθ=a の解を求める
  float alpha = asin(a); 
  float x1, x2; // 2つの解を格納する変数
  if(a >= 0.0){
    x1 = alpha;
    x2 = PI - alpha;
  } else {
    x1 = 2.0*PI + alpha;
    x2 = PI - alpha;
  }
  println(x1, x2);
  
  // y=sinθ（0≦θ＜2π)を描画
  stroke(0,0,0);
  float A = 1.0; // 振幅
  float k = 1.0; // θの係数
  float alpha1 = 0.0; // 位相
  float y1 = 0.0; // y軸方向の移動量
  draw_sin(A,k,alpha1,y1, x_min, x_max);
  
  // y=a（0≦θ＜2π)を描く
  draw_line(x_min, x_max, a);
  
  // 2つの解をプロット
  plot_point(x1, a);
  plot_point(x2, a);
}

// sinカーブ y=A sin(k(θ-alpha))+y1 を描く関数
void draw_sin(
  float A, // 振幅
  float k, // θの係数
  float alpha, // 位相
  float y1, // y軸方向の移動量
  float x_min, // グラフの定義域（最小値）
  float x_max  // グラフの定義域（最大値）
){
  // グラフの定義域
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // sinカーブ上の点のx座標
    y = A * sin( k*(x-alpha) ) + y1; // sinカーブ上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// x軸に平行な直線
void draw_line(
  float x_min, // グラフの定義域（最小値）
  float x_max, // グラフの定義域（最大値）
  float y // yの値
){
  float X_min = width / 2.0 / x_range * x_min;
  float X_max = width / 2.0 / x_range * x_max;
  float Y = height / 2.0 / y_range * y;
  line(X_min, Y, X_max, Y);
}

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード1　sin関数の方程式を解くプログラム

ここで、ソースコード1について解説しておきます。
① 上記「asin関数」の節で解説したように、sin 関数の方程式$${\sin \theta = a}$$の２つの解は$${a \geq 0}$$の場合と$${a < 0}$$の場合とで変わるので解を求める際に場合分けをしています。
② sin カーブを描く関数 draw_sin は、『高校数学をプログラミングで解く（数学II編）「3-4 三角関数のグラフ」』で作成したスケッチ「draw_sin_curve」内で作成したものを再利用していますが、今回、描画の際の定義域を指定できるように変数 x_min と x_max を引数で与えています。
③ $${\theta}$$軸に平行な直線を描く関数 draw_line を準備しました。
④ 平面上の指定された座標位置に点をプロットするための関数 plot_point を準備しました。

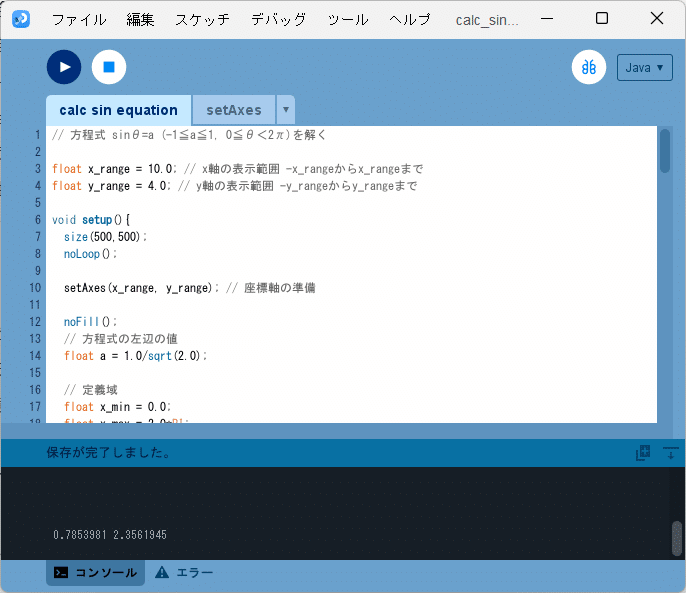
ソースコード1を、スケッチ「calc_sin_equation」の「calc_sin_equation」タブのテキストエディタ部分に書いて実行すると、図6のように、方程式の２つの解が開発環境ウィンドウのコンソールに

0.7853981 2.3561945

と出力されます。

また、図7のように、実行ウィンドウのキャンバス上に$${y=\sin \theta}$$のグラフと$${y=a}$$のグラフとが描かれ、方程式の解である２つの解（２つのグラフの交点）の位置に点がプロットされます。

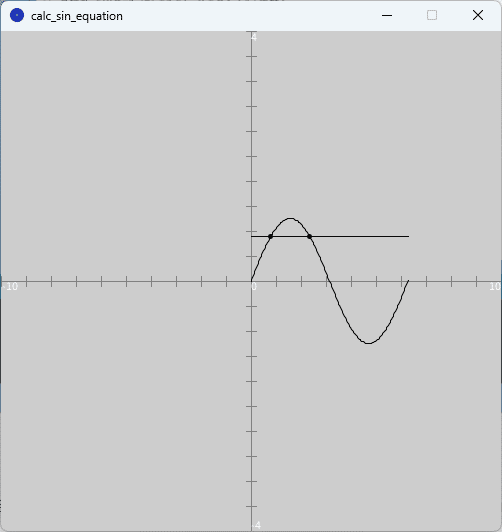
なお、横軸（$${\theta}$$軸方向）と縦軸（$${y}$$軸方向）とのスケールが異なっていることに注意してください。

cos関数の方程式を解くプログラム

次に、以下の cos 関数の方程式を解くプログラムを作成します。

$$
\cos \theta = \frac{1}{2} \ \ (0 \leq \theta < 2\pi)
$$

上記で作成したスケッチ「calc_sin_equation」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「calc_cos_equation」と変更し、またスケッチ「calc_cos_equation」内の「calc_sin_equation.pde」ファイルの名前を「calc_cos_equation.pde」に変更します。そして、pdeファイル「calc_cos_equation.pde」をダブルクリックしてスケッチ「calc_cos_equation」の開発環境ウィンドウを立ち上げます。
開発環境ウィンドウのタブ欄で「calc_cos_equation」タブを選択して、そのテキストエリアのソースコードを以下のような記述に変更します。

// 方程式 cosθ=a (-1≦a≦1, 0≦θ＜2π)を解く

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 4.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  // 方程式の左辺の値
  float a = 1.0/2.0;

  // 定義域
  float x_min = 0.0;
  float x_max = 2.0*PI;

  // 方程式 cosθ=1/2 の解を求める
  float alpha = acos(a);
  float x1, x2; // 2つの解を格納する変数
  x1 = alpha;
  x2 = 2.0*PI - alpha;
  println(x1, x2);

  // y=cosθ（0≦θ＜2π)を描画
  stroke(0,0,0);
  float A = 1.0; // 振幅
  float k = 1.0; // θの係数
  float alpha1 = 0.0; // 位相
  float y1 = 0.0; // y軸方向の移動量
  draw_cos(A,k,alpha1,y1, x_min, x_max);
  
  // y=a（0≦θ＜2π)を描く
  draw_line(x_min, x_max, a);
  
  // 2つの解をプロット
  plot_point(x1, a);
  plot_point(x2, a);
}

// cosカーブ y=A cos(k(θ-alpha))+y1 を描く関数
void draw_cos(
  float A, // 振幅
  float k, // θの係数
  float alpha, // 位相
  float y1, // y軸方向の移動量
  float x_min, // グラフの定義域（最小値）
  float x_max  // グラフの定義域（最大値）
){
  // グラフの定義域
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // sinカーブ上の点のx座標
    y = A * cos( k*(x-alpha) ) + y1; // sinカーブ上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// x軸に平行な直線
void draw_line(
  float x_min, // グラフの定義域（最小値）
  float x_max, // グラフの定義域（最大値）
  float y // yの値
){
  float X_min = width / 2.0 / x_range * x_min;
  float X_max = width / 2.0 / x_range * x_max;
  float Y = height / 2.0 / y_range * y;
  line(X_min, Y, X_max, Y);
}

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード2　cos関数の方程式を解くプログラム

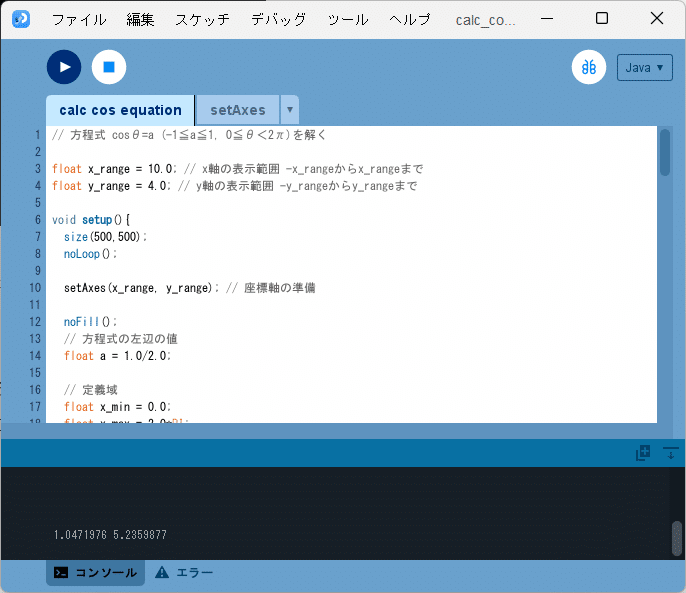
ソースコード2を、スケッチ「calc_cos_equation」の「calc_cos_equation」タブのテキストエディタ部分に書いて実行すると、図8のように、方程式の２つの解が開発環境ウィンドウのコンソールに

1.0471976 5.2359877

と出力されます。

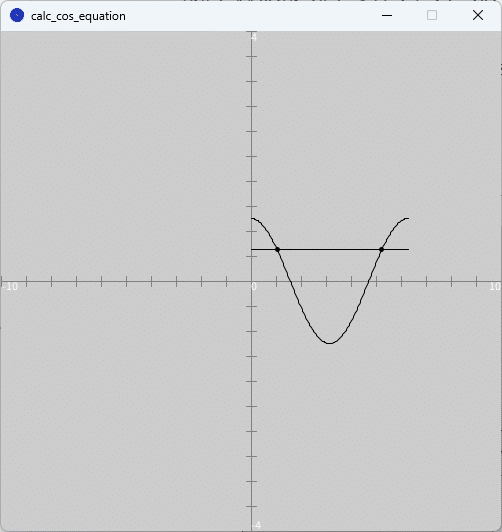
また、図9のように、実行ウィンドウのキャンバス上に$${y=\cos \theta}$$のグラフと$${y=a}$$のグラフとが描かれ、方程式の解である２つの解（２つのグラフの交点）の位置に点がプロットされます。

tan関数の方程式を解くプログラム

最後に、以下の tan 関数の方程式を解くプログラムを作成します。

$$
\tan \theta = -1 \ \ (0 \leq \theta < 2\pi)
$$

上記で作成したスケッチ「calc_sin_equation」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「calc_tan_equation」と変更し、またスケッチ「calc_tan_equation」内の「calc_sin_equation.pde」ファイルの名前を「calc_tan_equation.pde」に変更します。そして、pdeファイル「calc_tan_equation.pde」をダブルクリックしてスケッチ「calc_tan_equation」の開発環境ウィンドウを立ち上げます。
開発環境ウィンドウのタブ欄で「calc_tan_equation」タブを選択して、そのテキストエリアのソースコードを以下のような記述に変更します。

// 方程式 tanθ=a (0≦θ＜2π)を解く

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 4.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  // 方程式の左辺の値
  float a = -1.0;

  // 定義域
  float x_min = 0.0;
  float x_max = 2.0*PI;
  
  // 方程式 tanθ=-1 の解を求める
    float alpha = atan(a);
  float x1, x2; // 2つの解を格納する変数
  if(a >= 0.0){
    x1 = alpha;
    x2 = PI + alpha;
  } else {
    x1 = PI + alpha;
    x2 = 2.0*PI + alpha;
  }
  println(x1, x2);

  // y=tanθ（0≦θ＜2π)を描画
  stroke(0,0,0);
  float A = 1.0; // 振幅
  float k = 1.0; // θの係数
  float alpha1 = 0.0; // 位相
  float y1 = 0.0; // y軸方向の移動量
  draw_tan(A,k,alpha1,y1, x_min, x_max);
  
  // y=a（0≦θ＜2π)を描く
  draw_line(x_min, x_max, a);
  
  // 2つの解をプロット
  plot_point(x1, a);
  plot_point(x2, a);
}

// tanカーブ y=A tan(k(θ-alpha))+y1 を描く関数
void draw_tan(
  float A, // 振幅
  float k, // θの係数
  float alpha, // 位相
  float y1, // y軸方向の移動量
  float x_min, // グラフの定義域（最小値）
  float x_max  // グラフの定義域（最大値）
){
  // グラフの定義域
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // tanカーブ上の点のx座標
    y = A * tan( k*(x-alpha) ) + y1; // tanカーブ上の点のyの値
    if( abs(y) < 2.0*y_range ){
      // キャンバス上の座標位置に換算
      X = width / 2.0 / x_range * x;
      Y = height / 2.0 / y_range * y;
      vertex(X, Y);
    } else {
      endShape();
      beginShape();
    }
  }
  endShape();

}

// x軸に平行な直線
void draw_line(
  float x_min, // グラフの定義域（最小値）
  float x_max, // グラフの定義域（最大値）
  float y // yの値
){
  float X_min = width / 2.0 / x_range * x_min;
  float X_max = width / 2.0 / x_range * x_max;
  float Y = height / 2.0 / y_range * y;
  line(X_min, Y, X_max, Y);
}

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード3　tan関数の方程式を解くプログラム

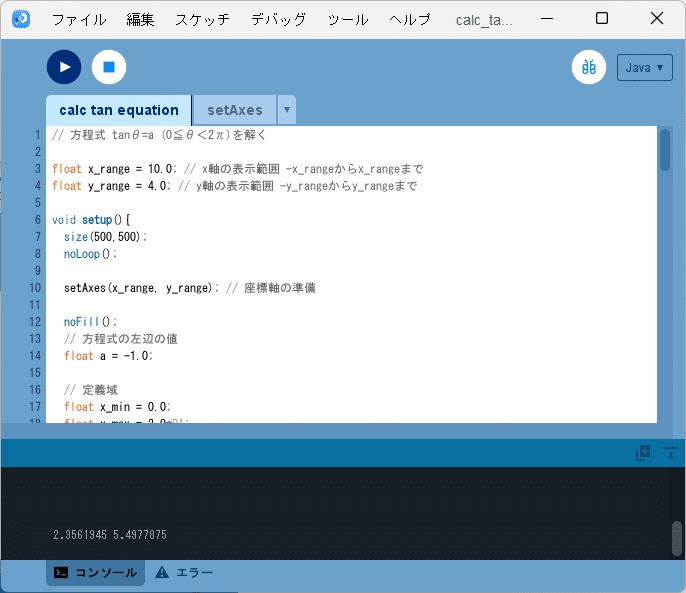
ソースコード3を、スケッチ「calc_tan_equation」の「calc_tan_equation」タブのテキストエディタ部分に書いて実行すると、図10のように、方程式の２つの解が開発環境ウィンドウのコンソールに

2.3561945 5.4977875

と出力されます。

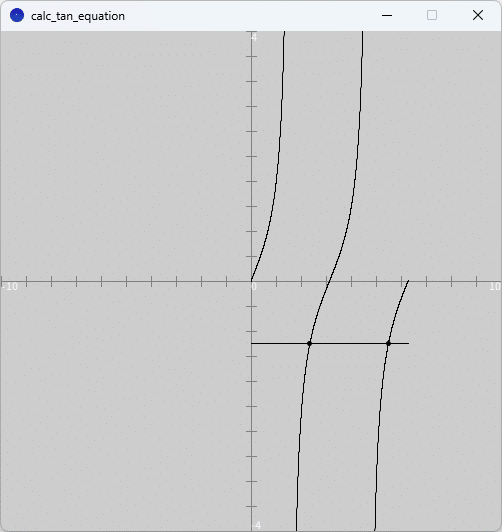
また、図11のように、実行ウィンドウのキャンバス上に$${y=\tan \theta}$$のグラフと$${y=a}$$のグラフとが描かれ、方程式の解である２つの解（２つのグラフの交点）の位置に点がプロットされます。

まとめ

今回は、数学IIで学ぶ「三角関数の応用」について、三角関数の方程式を解くためのプログラムを作成しました。
三角関数の方程式を解くためには、asin関数、acos関数、atan関数を利用すると、三角関数の方程式の1つの解を得ることができます。ただ、方程式の解の範囲が$${0 \leq \theta < 2\pi}$$のように指定されている場合はそのままその解を利用することができないことがあります。この場合は指定された範囲に収まるように調整が必要でした。これは、三角関数の方程式を解く際にポイントとなるところですので、是非覚えておいてください。

参考文献

改訂版教科書傍用スタンダード数学II（数研出版、ISBN9784410209369）

この記事が気に入ったらサポートをしてみませんか？