
高校数学をプログラミングで解く(数学II編)「3-4 三角関数のグラフ」
マガジンリスト > 数学Ⅱ編 3.三角関数 > 3-4 三角関数のグラフ
はじめに
今回は、数学IIで学ぶ「三角関数のグラフ」について、sinカーブやcosカーブを描くためのプログラムを作成します。
三角関数のグラフ
まず、三角関数のグラフについて解説しておきます。
周期関数
① $${x}$$のどんな値に対しても$${f(x+p)=f(x)}$$が成り立つとき、$${f(x)}$$は$${p}$$を周期とする周期関数である。普通、周期といえば正で最小のものを指す。
② $${f(x)}$$の周期が$${p}$$のとき、$${f(kx)}$$の周期は$${p/|k| \ \ [k \neq 0]}$$
関数の性質
① 奇関数 $${f(-x)=-f(x)}$$ $${y=f(x)}$$のグラフは原点に関して対称。
② 偶関数 $${f(-x)=f(x)}$$ $${y=f(x)}$$のグラフは$${y}$$軸に関して対称。
三角関数のグラフ
$$
\begin{array}{c|c|c|c}
& y=\sin \theta & y=\cos \theta & y=\tan \theta \\
\hline
\mathrm{周期} & 2\pi & 2\pi & \pi \\
\mathrm{値域} & -1 \leq y \leq 1 & -1 \leq y \leq 1 & \mathrm{実数全体} \\
\mathrm{グラフ} & \mathrm{原点対称(奇関数)}& y\mathrm{軸対称(偶関数)} & \mathrm{原点対称(奇関数)}
\end{array}
$$
sin関数のグラフを描く
では、$${\sin}$$関数のグラフを描いてみます。
問題1
以下のグラフを括弧に指定された色で描け。
(1) $${y=\sin \theta}$$(黒色)
(2) $${y=4 \sin \theta}$$(赤色)
(3) $${y=\sin 4 \theta}$$(緑色)
(4) $${y=2 \sin 2 \theta}$$(青色)
アルゴリズム設計
三角関数のグラフを描く際、以下のような形の関数をベースに考えると描きやすくなります。
$$
y = A \sin (k ( \theta - \alpha) ) + y_1
$$
ここで、$${A}$$は振幅と呼ばれ、三角関数のグラフの上下の振り幅を決めます。$${k}$$は三角関数のグラフの周期を決めるもので、実際周期は$${2 \pi/|k|}$$となります。$${\alpha}$$は位相と呼ばれ、平面上の$${\theta}$$方向にグラフ全体をどれだけ移動するかを決める値となります。$${y_1}$$は、平面上の$${y}$$方向にグラフ全体をどれだけ移動するかを決める値となります。
今回は、このベースとなる関数のグラフを描くための関数を準備して、各グラフを描くようにしていきます。
プログラム
では、問題1のsinカーブのグラフを描くプログラムを作成します。
グラフを描くために以前準備した 座標軸を描くための関数 setAxes を利用しますので、記事『高校数学をプログラミングで解く(数学I編)「1-0-2 グラフを描くための準備(その2)」』で作成したスケッチ「drawFunction」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「draw_sin_curve」と変更し、またスケッチ「draw_sin_curve」内の「drawFunction.pde」ファイルの名前を「draw_sin_curve.pde」に変更します。そして、pdeファイル「draw_sin_curve.pde」をダブルクリックしてスケッチ「draw_sin_curve」の開発環境ウィンドウを立ち上げます。
開発環境ウィンドウのタブ欄で「draw_sin_curve」タブを選択して、そのテキストエリアのソースコードを以下のような記述に変更します。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
// (1) y=sinθ
stroke(0,0,0);
float A = 1.0; // 振幅
float k = 1.0; // θの係数
float alpha = 0.0; // 位相
float y1 = 0.0; // y軸方向の移動量
draw_sin(A,k,alpha,y1);
// (2) y=4sinθ
stroke(255,0,0);
A = 4.0; // 振幅
k = 1.0; // θの係数
alpha = 0.0; // 位相
y1 = 0.0; // y軸方向の移動量
draw_sin(A,k,alpha,y1);
// (3) y=sin4θ
stroke(0,255,0);
A = 1.0; // 振幅
k = 4.0; // θの係数
alpha = 0.0; // 位相
y1 = 0.0; // y軸方向の移動量
draw_sin(A,k,alpha,y1);
// (4) y=2sin2θ
stroke(0,0,255);
A = 2.0; // 振幅
k = 2.0; // θの係数
alpha = 0.0; // 位相
y1 = 0.0; // y軸方向の移動量
draw_sin(A,k,alpha,y1);
}
// sinカーブ y=A sin(k(θ-alpha))+y1 を描く関数
void draw_sin(
float A, // 振幅
float k, // θの係数
float alpha, // 位相
float y1 // y軸方向の移動量
){
// グラフの定義域
float x_min = -x_range;
float x_max = x_range;
int plot_num = 200; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // sinカーブ上の点のx座標
y = A * sin( k*(x-alpha) ) + y1; // sinカーブ上の点のyの値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}ソースコード1 問題1の4つのsinカーブを描くプログラム
ベースとなる関数$${y = A \sin (k ( \theta - \alpha) ) + y_1}$$を draw_sin 関数として準備しました。引数は$${A, k, \alpha, y_1}$$をとり、この4つの値でsinカーブの形が決まります。
ソースコード1を、スケッチ「draw_sin_curve」の「draw_sin_curve」タブのテキストエディタ部分に書いて実行すると、図1のように、実行ウィンドウのキャンバス上に問題1の4つのsinカーブが描かれます。
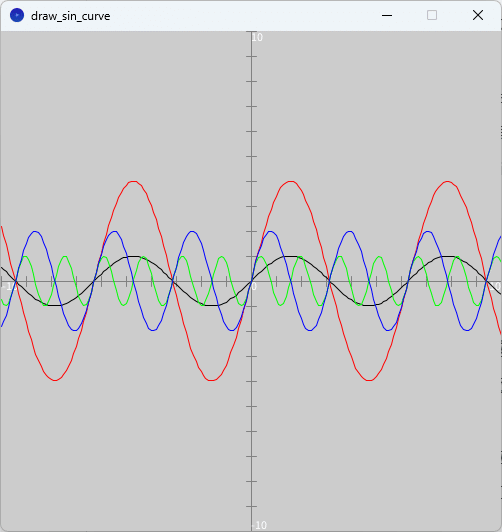
cos関数のグラフを描く
次に、$${\cos}$$関数のグラフを描いてみます。
問題2
以下のグラフを括弧に指定された色で描け。
(1) $${y= \cos \theta}$$(黒色)
(2) $${y= \cos ( \theta - \frac{\pi}{4})}$$(赤色)
(3) $${y= \cos \theta - 1}$$(緑色)
(4) $${y=3 \cos \frac{\theta}{3}}$$(青色)
アルゴリズム設計
今回も、以下のような形の関数をベースに考えて描いていきます。
$$
y = A \cos (k ( \theta - \alpha) ) + y_1
$$
各係数は、sinカーブのときと同じです。
プログラム
では、問題2のcosカーブのグラフを描くプログラムを作成します。
先程作成したスケッチ「draw_sin_curve」を再利用します。スケッチ「draw_sin_curve」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「draw_cos_curve」と変更し、またスケッチ「draw_cos_curve」内の「draw_sin_curve.pde」ファイルの名前を「draw_cos_curve.pde」に変更します。そして、pdeファイル「draw_cos_curve.pde」をダブルクリックしてスケッチ「draw_cos_curve」の開発環境ウィンドウを立ち上げます。
開発環境ウィンドウのタブ欄で「draw_cos_curve」タブを選択して、そのテキストエリアのソースコードを以下のような記述に変更します。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
// (1) y=cosθ
stroke(0,0,0);
float A = 1.0; // 振幅
float k = 1.0; // θの係数
float alpha = 0.0; // 位相
float y1 = 0.0; // y軸方向の移動量
draw_cos(A,k,alpha,y1);
// (2) y=cos(θ-π/4)
stroke(255,0,0);
A = 1.0; // 振幅
k = 1.0; // θの係数
alpha = PI/4.0; // 位相
y1 = 0.0; // y軸方向の移動量
draw_cos(A,k,alpha,y1);
// (3) y=cosθ-1
stroke(0,255,0);
A = 1.0; // 振幅
k = 1.0; // θの係数
alpha = 0.0; // 位相
y1 = -1.0; // y軸方向の移動量
draw_cos(A,k,alpha,y1);
// (4) y=3cos(θ/3)
stroke(0,0,255);
A = 3.0; // 振幅
k = 1.0/3.0; // θの係数
alpha = 0.0; // 位相
y1 = 0.0; // y軸方向の移動量
draw_cos(A,k,alpha,y1);
}
// cosカーブ y=A cos(k(θ-alpha))+y1 を描く関数
void draw_cos(
float A, // 振幅
float k, // θの係数
float alpha, // 位相
float y1 // y軸方向の移動量
){
// グラフの定義域
float x_min = -x_range;
float x_max = x_range;
int plot_num = 200; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // cosカーブ上の点のx座標
y = A * cos( k*(x-alpha) ) + y1; // cosカーブ上の点のyの値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}ソースコード2 問題2の4つのcosカーブを描くプログラム
ベースとなる関数$${y = A \cos (k ( \theta - \alpha) ) + y_1}$$を draw_cos 関数として準備しました。
ソースコード2を、スケッチ「draw_cos_curve」の「draw_cos_curve」タブのテキストエディタ部分に書いて実行すると、図2のように、実行ウィンドウのキャンバス上に問題2の4つのcosカーブが描かれます。
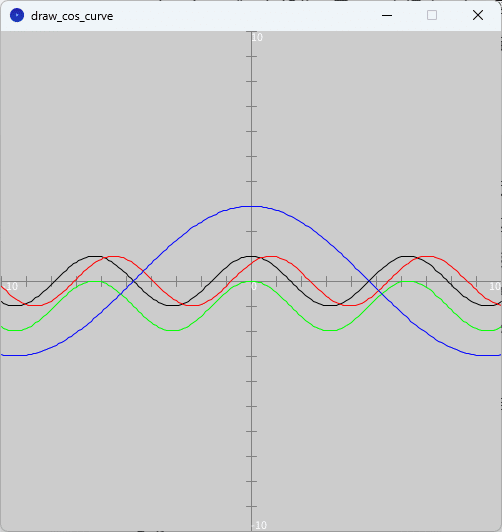
tan関数のグラフを描く
最後に、$${\tan}$$関数のグラフを描いてみます。
問題3
以下のグラフを括弧に指定された色で描け。
(1) $${y= \tan \theta}$$(黒色)
(2) $${y= 2 \tan ( \theta - \frac{\pi}{4})+1}$$(赤色)
アルゴリズム設計
$${\tan}$$関数についても、以下のような形の関数をベースに考えて描いていきます。
$$
y = A \tan (k ( \theta - \alpha) ) + y_1
$$
各係数は、sinカーブのときと同じです。
ただ、$${\tan}$$関数を描く場合、注意が必要です。それは、
$$
k ( \theta - \alpha) = \frac{\pi}{2} + n \pi \ \ (n\mathrm{は整数})
$$
を満たす$${\theta}$$の位置で$${\tan (k ( \theta - \alpha) )}$$の値は発散します。そのため、今回のプログラムでは、上記のベースとなる関数の値の大きさがキャンバス上に用意した$${y}$$軸方向の範囲(プログラムでは変数 y_range の値)の2倍を越えたらグラフを描かないようにしています。
プログラム
では、問題3のtanカーブのグラフを描くプログラムを作成します。
先程作成したスケッチ「draw_sin_curve」を再利用します。スケッチ「draw_sin_curve」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「draw_tan_curve」と変更し、またスケッチ「draw_tan_curve」内の「draw_sin_curve.pde」ファイルの名前を「draw_tan_curve.pde」に変更します。そして、pdeファイル「draw_tan_curve.pde」をダブルクリックしてスケッチ「draw_tan_curve」の開発環境ウィンドウを立ち上げます。
開発環境ウィンドウのタブ欄で「draw_tan_curve」タブを選択して、そのテキストエリアのソースコードを以下のような記述に変更します。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
// (1) y=tanθ
stroke(0,0,0);
float A = 1.0; // 振幅
float k = 1.0; // θの係数
float alpha = 0.0; // 位相
float y1 = 0.0; // y軸方向の移動量
draw_tan(A,k,alpha,y1);
// (2) y=2tan(θ-π/4)+1
stroke(255,0,0);
A = 2.0; // 振幅
k = 1.0; // θの係数
alpha = PI/4.0; // 位相
y1 = 1.0; // y軸方向の移動量
draw_tan(A,k,alpha,y1);
}
// tanカーブ y=A tan(k(θ-alpha))+y1 を描く関数
void draw_tan(
float A, // 振幅
float k, // θの係数
float alpha, // 位相
float y1 // y軸方向の移動量
){
// グラフの定義域
float x_min = -x_range;
float x_max = x_range;
int plot_num = 2000; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // tanカーブ上の点のx座標
y = A * tan( k*(x-alpha) ) + y1; // tanカーブ上の点のyの値
if( abs(y) < 2.0*y_range ){
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
} else {
endShape();
beginShape();
}
}
endShape();
}ソースコード3 問題3の2つのtanカーブを描くプログラム
ベースとなる関数$${y = A \tan (k ( \theta - \alpha) ) + y_1}$$を draw_tan 関数として準備しました。アルゴリズム設計のところで説明したように、tan関数の値(変数 y の値)の大きさが 2.0*y_range を越えた場合は一旦グラフの描画を終了し、その後、tan関数の値の大きさが 2.0*y_range より小さい値になったらグラフの描画を再開するということを繰り返して描いています。
ソースコード3を、スケッチ「draw_tan_curve」の「draw_tan_curve」タブのテキストエディタ部分に書いて実行すると、図3のように、実行ウィンドウのキャンバス上に問題3の2つのtanカーブが描かれます。

まとめ
今回は、数学IIで学ぶ「三角関数のグラフ」について、sinカーブやcosカーブを描くためのプログラムを作成しました。
三角関数のグラフを描くためのベースとなる関数は、$${y = A \sin (k ( \theta - \alpha) ) + y_1}$$の形になります。この関数で描かれるグラフは、$${y=\sin \theta}$$のグラフに対して、振幅、周期、位相などを調整したものと考えることができます。このような関係性を理解した上でグラフを描いていくことは今後に役立つと思いますので、是非そのような観点で今回の問題以外のグラフも描いてみてください。
また、今回はtanカーブに対して漸近線を描きませんでした。漸近線などを描くともう少しtanカーブの結果が見やすくなりますので、こちらも是非チャレンジしてみてください。
参考文献
改訂版 教科書傍用 スタンダード 数学II(数研出版、ISBN9784410209369)
